Механизм буферного действия

Причины буферного действия заключаются в следующем. Ионы Н⁺ или ОН^–, которые добавляются к буферу, не остаются свободными, а связываются в молекулы слабого электролита.

Проиллюстрируем механизм буферного действия на примере ацетатного буфера, который состоит из CH₃COOH и CH₃COONa. В растворе ацетатного буфера имеют место равновесия:

CH₃COOH ↔ CH₃COO^– + H⁺

CH₃COONa → CH₃COO^– + Na⁺

При добавлении к нему небольшого количества сильной кислоты ионы Н⁺ связываются с ацетат-ионами в молекулы слабой уксусной кислоты, в результате чего значение рН практически не меняется:

CH₃COO^– + H⁺ ↔ CH₃COOH

При добавлении небольшого количества щелочи ионы ОН^– связываются с ионами H⁺, образуя молекулы воды, поэтому значение рН тоже практически не меняется:

H⁺ + ОН^– ↔ Н₂О

В фосфатном буфере, состоящем из двух солей NaH₂PO₄ и Na₂HPO₄, оба компонента диссоциированы на ионы:

NaH₂PO₄ → Na⁺ + H₂PO₄^–

Na₂HPO₄ → 2Na⁺ + HPO₄^2–

При добавлении Н⁺ гидрофосфат переходит в дигидрофосфат, связывая поступившие протоны:

HPO₄^2– + H⁺ ↔ H₂PO₄^–

При добавлении ОН^– происходит кислотно-основная реакция с участием дигидрофосфата, в ходе которой ионы ОН^– связываются в молекулы Н₂О:

H₂PO₄^– + ОН^– ↔ HPO₄^2– + Н₂О

Использование буферных растворов

Буферные растворы используют во всех случаях проведения химических реакций и технологических процессов, когда требуется поддерживать постоянное значение рН в ходе их проведения.

Ход многих аналитических химических реакций, которые используются для обнаружения и разделения, зависит от рН среды, поэтому для поддержания необходимого значения рН используют буферные растворы. В особенности это касается следующих реакций:

1) С участием анионов слабых кислот или катионов слабых оснований. Например, групповые разделения – осаждение катионов II аналитической группы, III аналитической группы с помощью групповых реактивов – проводятся только в аммиачном буфере [3]. Реакции обнаружения ионов Mg²⁺ c Na₂HPO₄, PO₄^3– с Mg²⁺, Ba²⁺ с K₂Cr₂O₇ и многие другие также проводятся в среде рН-буферов [3].

2) Цветных качественных реакций с органическими реагентами. Например, при обнаружении ионов Al³⁺ капельной реакцией с ализарином необходимо, помимо анализируемого раствора и реактива, нанести на полоску фильтровальной бумаги HCl и поместить ее над емкостью с конц. NH₄OH (первый компонент аммиачного буфера). При взаимодействии кислоты и слабого основания образуется второй компонент буфера – NH₄Cl, и тем самым создаются необходимые условия для протекания цветной реакции [3].

При проведении определения с использованием метода комплексонометрического титрования важнейшим условием также является присутствие буфера в титруемом растворе.

Буферные растворы образуются в ходе кислотно-оснóвного титрования слабых протолитов и их смесей до точки эквивалентности или между двумя точками эквивалентности.

Примеры использования буферов в химической технологии и полиграфии:

§ в офсетной печати используется фосфатный буфер с рН = 6,8;

§ в гальванопроцессах используется борный буфер с рН » 5 и т. д.

В крови человека тоже есть рН-буфер с рН = 7,3–7,5, состоящий из Н₂СО₃ и НСО₃^–. Если значение рН крови по каким-либо причинам не укладывается в данный интервал, то это приводит к летальному исходу.

Расчет рН буферных смесей

1. Буферный раствор на основе слабой
кислоты и ее соли

Рассмотрим расчет значения рН на примере цианидного буфера, состоящего из HCN и NaCN. В растворе оба компонента диссоциируют, причем соль полностью:

NaCN → Na⁺ + CN^–,

а кислота – обратимо:

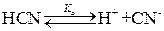
Запишем выражение для константы равновесия:

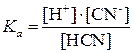Þ

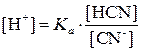(3.14)

Поскольку степень диссоциации (α) слабой кислоты мала, то можно сделать допущение, что равновесная концентрация недиссоциированной кислоты равна ее общей концентрации в растворе:

[HCN] » C_кисл.

Кроме того, равновесную концентрацию цианид-ионов можно принять практически равной общей концентрации соли

[CN^–] » C_соли,

поскольку NaCN, как сильный электролит, диссоциирует полностью. При этом диссоциация слабой кислоты подавляется за счет поступления ионов CN^– из соли.

Подставим эти выражения в формулу (3.14) и получим:

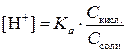Þ

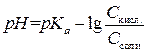(3.15)

Используя эту расчетную формулу, можно объяснить также свойства буферных растворов:

§ «Значение рН буферного раствора не меняется при разбавлении». Как видно из формулы (3.15), если раствор разбавить в n раз, то концентрация обоих компонентов буфера тоже уменьшится в n раз, однако отношение концентраций останется постоянным Þ значение рН не изменится. Однако, при очень сильном разбавлении (³ 10⁴ раз) значение рН меняется на 0,5–1,0 ед. рН.

§ «Значение рН буферного раствора мало меняется при добавлении небольших количеств Н⁺ или ОН^–». При добавлении небольшого количества Н⁺ концентрация слабой кислоты несколько увеличивается, а концентрация соли – уменьшается. При этом отношение концентраций компонентов буфера немного меняется, но логарифм этого отношения меняется очень незначительно Þ значение рН практически не изменяется. Если же добавить к буферу небольшое количество ОН^–, то концентрация слабой кислоты несколько уменьшится, а концентрация соли – увеличивается, но логарифм этого отношения меняется очень незначительно Þ значение рН также практически не изменяется.

2. Буферный раствор на основе слабого
основания и его соли

Рассмотрим расчет значения рН на примере аммиачного буфера, состоящего из NH₄OH и NH₄Cl. В растворе оба компонента диссоциируют, причем соль полностью:

NH₄Cl → NH₄⁺ + Cl^–

а основание – обратимо:

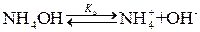
Запишем выражение для константы равновесия:

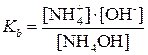Þ

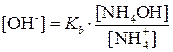(3.16)

Поскольку степень диссоциации (α) слабого основания мала, то можно сделать допущение, что равновесная концентрация недиссоциированного основания равна его общей концентрации в растворе:

[NH₄OH] » C_осн.

Кроме того, равновесную концентрацию ионов NH₄⁺ можно принять практически равной общей концентрации соли

[NH₄⁺] » C_соли,

поскольку NH₄Cl, как сильный электролит, диссоциирует полностью. При этом диссоциация слабого основания подавляется за счет поступления ионов NH₄⁺ из соли.

Подставим эти выражения в формулу (3.16) и получим:

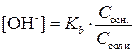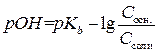Þ

Þ

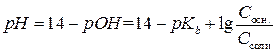(3.17)

3. Буферный раствор на основе двух солей многоосновной кислоты

Рассмотрим расчет значения рН на примере фосфатного буфера, состоящего из NaH₂PO₄ и Na₂HPO₄. В этой системе дигидрофосфат натрия NaH₂PO₄, имеющий больше ионов H⁺, выступает в роли кислоты по отношению к своей соли – гидрофосфату натрия Na₂HPO₄ (меньше ионов H⁺).

Следовательно, для расчета значения рН необходимо воспользоваться формулой (3.15). Для выяснения вопроса, какое значение pK_a фосфорной кислоты надо подставить в формулу, запишем равновесие между компонентами буфера:

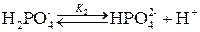
Следовательно, необходимо подставить pK_a,2. Тогда расчетная формула примет вид:

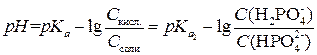
Буферная емкость

Способность буферных растворов поддерживать значение рН постоянным не безгранична. Любой буферный раствор обладает определенной буферной емкостью.

Буферная емкость – это такое количество моль эквивалентов сильной кислоты или сильного основания, которое нужно добавить к 1 л буферной раствора, чтобы изменить его значение рН на 1 ед.:

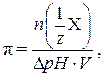
где 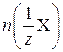– количество моль экв. кислоты или щелочи; ΔрН – изменение рН после добавления кислоты или щелочи; V – объем буферного раствора, л.

Чем больше буферная емкость, тем лучше буфер удерживает постоянным значение рН.

Факторы, влияющие на буферную емкость:

§ суммарная концентрация компонентов смеси: чем она больше, тем больше буферная емкость;

§ соотношение концентраций компонентов буфера: чем ближе к 1 значение

,

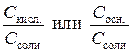тем больше буферная емкость, поэтому максимальная буферная емкость достигается при одинаковых концентрациях компонентов:

С_кисл. = С_соли или С_осн. = С_соли

В этих случаях, согласно формулам (3.15) и (3.17) значения рН буферных растворов равны:

pH = pK_a или pH = 14 – pK_b

На практике обычно готовят буферы со значениями рН

pH = pK_a ± 1 или pH = (14 – pK_b) ± 1

Для этого задают отношения концентраций компонентов буферной смеси

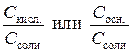
в интервале от 10 : 1 до 1 : 10. Рецептуры для приготовления буферных растворов с различными значениями рН приводятся в справочнике [1]. Методики определения буферной емкости изложены в [5].