Действующие значения тока и напряжения
Для описания характеристик переменного тока необходимо избрать определённые физические величины. Мгновенные и амплитудные значения для этих целей неудобны, а средние значения за период равны нулю. Поэтому вводят понятие действующих значений тока и напряжения. Они основаны на тепловом действии тока, не зависящем от его направления.
Действующими значениями тока и напряжения называют соответствующие параметры такого постоянного тока, при котором в данном проводнике за данный промежуток времени выделяется столько же теплоты, что и при переменном токе. Найдем соотношение между действующими и амплитудными значениями.
В активном сопротивлении R при постоянном токе I за период постоянного тока T по закону Джоуля-Ленца выделится следующее количество теплоты:
Q=I RT (1.4)
При переменном токе i в том же сопротивлении R за бесконечно малый промежуток времени dt выделится следующее количество теплоты:
dQ = i Rdt (1.5)
где мгновенное значение тока i определяется формулой:
i = I0sinωt (1.6)
Тогда теплота, выделяемая переменным током за период Т равна:
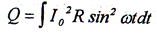

Интеграл (1.7) вычисляется следующим образом:
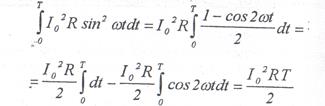
Второй интеграл равен нулю, поскольку это интеграл от периодической функции за один период. Приравняв, согласно определению (1.4) и (1.8), получим:
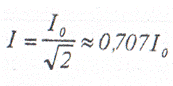
Таким образом, действующее значение переменного тока в √2 раз меньше его амплитудного значения. Аналогично вычисляются действующие значения напряжения и ЭДС:
U = U0/√2; E = E0/√2 (1.10)
Действующие значения обозначаются прописными латинскими буквами без индексов.
Метод векторных диаграмм
Метод векторных диаграмм – то есть изображение величин, характеризующих переменный ток векторами, а не тригонометрическими функциями, чрезвычайно удобен.
Переменный ток, в отличие от постоянного, характеризуется двумя скалярными величинами – амплитудой и фазой. Поэтому для математического описания переменного тока необходим математический объект, также характеризуемый двумя скалярными величинами. Существуют два таких математических объектов – это вектор на плоскости и комплексное число. В теории электрических цепей и те и другие используются для описания переменных токов.
При описании электрической цепи переменного тока с помощью векторных диаграмм каждому току и напряжению сопоставляется вектор на плоскости в полярных координатах, длина которого равна амплитуде тока или напряжения, а полярный угол равен соответствующей фазе. Поскольку фаза переменного тока зависит от времени, то считается, что все векторы вращаются против часовой стрелки с частотой переменного тока. Векторная диаграмма строится для фиксированного момента времени.
Более подробно построение и использование векторных диаграмм будет изложено ниже на примерах конкретных цепей.
