Энергия электрического поля. Если обкладки заряженного конденсатора замкнуть металлическим проводником, то в нем возникнет электрический ток

Если обкладки заряженного конденсатора замкнуть металлическим проводником, то в нем возникнет электрический ток, а конденсатор разрядится. Электрический ток разряда конденсатора выделяет в проводнике определенное количество теплоты, а это значит, что заряженный конденсатор обладает энергией. Найдем эту энергию.

Предположим, что конденсатор бесконечно медленно заряжается от батареи. При этом совершается работа

dA=udq.

Или, используя определение емкости,

dA=Cudu.

Эта работа идет на увеличение энергии конденсатора dW. Тогда полная энергия, полученная конденсатором при зарядке от напряжения равного нулю до конечного значения U, найдется так

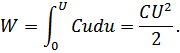
Таким образом

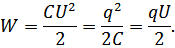
Благодаря способности запасать в себе энергию конденсаторы играют большую роль в электро- и радиотехнике.

Вообще, под емкостью проводника часто понимают его способность накапливать электрическую энергию.

Выражение (1) определяет полную энергию, запасенную в конденсаторе. С другой стороны, это энергия электрического поля, которое сосредоточено в области пространства, ограниченного пластинами конденсатора. В идеальном случае поля вне пластин нет. Поэтому можно говорить о плотности энергии электрического поля, не задумываясь о том, каким образом это поле создано. Емкость плоского конденсатора

В данном случае электрическое поле однородно. Разность потенциалов в однородном поле U=Ed. Тогда из (1) получим

где Е – полное электрическое поле внутри конденсатора, V – объем конденсатора, а ε - диэлектрическая проницаемость среды, заполняющей пространство между пластинами. Тогда для плотности энергии любого однородного электрического поля будет справедливо выражение

В случае неоднородного электрического поля полную энергию этого поля можно рассчитать по формуле

В заключении отметим, что эти формулы справедливы в случае однородного диэлектрика.