Работа и мощность постоянного тока. Закон Джоуля-Ленца

Электрический ток совершает в любом участке цепи определенную работу. Пусть имеется произвольный участок цепи, между концами которого существует напряжение U. По определению электрического напряжения работа, совершаемая при перемещении единицы заряда между точками а и б, равна U. Если сила тока в участке цепи равна i, то за время t пройдет заряд it, и поэтому работа электрического тока в этом участке будет

А = Uit. (1)

Это выражение справедливо для постоянного тока в любом случае, для какого угодно участка цепи, который может содержать проводники 1-го и 2-го рода, электромоторы и т.д.

Мощность тока, т.е. работа в единицу времени, равна

Р = A/t = Ui. (2)

Формулу (2) используют в системе СИ для определения единицы напряжения. Единица напряжения вольт (В) есть 1 В = 1 Вт/1 А = 1 Вт/А.

Вольт — электрическое напряжение, вызывающее в электрической цепи постоянный ток силой 1 А при мощности 1 Вт.

Будем теперь считать, что участок цепи представляет собой неподвижный проводник 1-го рода. Тогда вся работа тока превращается в тепло, которое выделяется в проводнике. Если проводник однороден и подчиняется закону Ома (сюда относятся все металлы и электролиты), то U = iг, где г — сопротивление проводника. В таком случае

А = ri²t. (3)

Этот закон был впервые установлен на опыте Э-Х. Ленцем и, независимо от него, Джоулем.

Отметим, что нагревание проводников током находит многочисленные технические применения. Наиболее важное – нагревательные приборы и осветительные лампы накаливания.

3.5. Источники тока. Сторонние силы.

Для того, чтобы в проводнике возник электрический ток необходимо, чтобы на носители зарядов действовала направленная сила. Легко видеть, что нельзя получить в проводнике постоянный ток, если для создания напряжения на концах проводника пользоваться заряженными конденсаторами. Действительно, наличие тока будет всегда сопровождаться переходом зарядов с одной обкладки на другую и притом в таком направлении, что заряды обкладок будут уменьшаться. В результате будет непрерывно уменьшаться напряжение между обкладками и, согласно закону Ома, сила тока в проводнике будет падать.

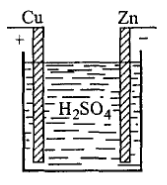Для получения постоянного тока на заряды в электрической цепи должны действовать какие-либо силы, отличные от сил электростатического поля. Такие силы получили общее название сторонних сил. Всякое устройство, в котором возникают сторонние силы, называют источником тока. Например, гальванические элементы – химические источники тока. На рис. показан один из простейших элементов — элемент Вольты. Он состоит из медной и цинковой пластин, называемых электродами элемента, погруженных в слабый водный раствор серной кислоты. Медь заряжается положительно, а цинк — отрицательно. Положительный электрод часто называют анодом, а отрицательный — катодом.

Когда какой-либо гальванический элемент создает в цепи ток, то внутри элемента происходят химические реакции. В большинстве элементов основная реакция состоит в соединении цинкового электрода, являющегося катодом элемента, с электролитом, и поэтому во время работы элемента расходуется металлический цинк, а в растворе появляются новые вещества -

продукты реакций. В элементе Вольты эта реакция такова:

Zn + H₂SO₄ = ZnSO₄ + Н₂

При всякой химической реакции либо поглощается, либо выделяется определенное количество энергии. Если предполагать, что химическая реакция происходит при постоянном внешнем давлении. При этом выделяется количество теплоты Q, равное Q=pm, где m — масса прореагировавшего вещества. Величина р определяет тепловой эффект химической реакции и указывает, какое количество теплоты выделяется при вступлении в данную реакцию единицы массы рассматриваемого вещества. Если реакция идет с выделением тепла, то р положительно (экзо-), если с поглощением тепла, — отрицательно (эндо-). Так, например, в указанной реакции р>0.

3.6. Электродвижущая сила. Закон Ома для полной цепи.

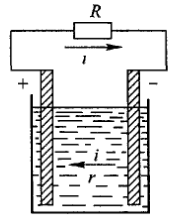
Рассмотрим теперь какой-либо гальванический элемент, замкнутый на проводник с сопротивлением R. При наличии тока масса электрода, перешедшая в электролит, равна

m = Kq,

где К — электрохимический эквивалент металла электрода, а q — полный заряд, прошедший через элемент. Поэтому для энергии, освобождаемой в химических реакциях у обоих электродов, имеем

Q= (p₁K₁ + P₂K₂)q.

При замкнутом элементе в цепи будет совершаться еще работа тока, которая будет превращаться в тепло Джоуля- Ленца. При этом мы должны учесть, что электрические заряды нигде не накапливаются в цепи, а, значит, ток существует не только во внешней цепи, но и внутри элемента. Гальванический элемент представляет для тока определенное сопротивление, называемое внутренним сопротивлением, которое складывается из сопротивлений электролита и электродов.

Однако если температура элемента поддерживается постоянной, то при

наличии тока элемент будет передавать окружающей среде (или, наоборот, заимствовать от нее) некоторое количество теплоты Q_t, необходимое для поддержания постоянства температуры.

Применим теперь к рассматриваемой замкнутой цепи первое начало термодинамики (общий закон сохранения энергии). Тогда Q= А + Q_T, где А — работа тока. Мы видим, что в работу тока превращается не вся энергия химических реакций, а лишь разность

А = Q - Q_T.

Величина А для называется максимальной работой химической реакции. Максимальная работа при данной температуре представляет собой определенную долю энергии Q и, подобно Q, пропорциональна заряду, прошедшему по цепи.

Поэтому можно положить

А =eq,

где e — максимальная работа данной химической реакции, рассчитанная на единицу заряда. Она получила название электродвижущей силы гальванического элемента.

Приравнивая А полной работе тока (во внешней цепи и внутри источника), имеем

eq = Ri²t + ri²t,

где г — внутреннее сопротивление элемента. Деля обе части равенства на заряд q = it, находим

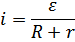
Полученный закон называется законом Ома для замкнутой цепи. Сумму (R+r) внешнего и внутреннего сопротивлений называют полным сопротивлением цепи.

Из формулы видно, что размерность e совпадает с размерностью напряжения, и поэтому ЭДС выражают в тех же единицах, что и напряжение.

ЭДС гальванического элемента зависит только от рода веществ, входящих в его состав. А внутреннее сопротивление элемента, как и всякого проводника, зависит от его размеров и формы.

Этот закон имеет общее значение. Всякий источник тока можно охарактеризовать его электродвижущей силой таким образом, что будет справедлив закон Ома. Так как ЭДС любого источника легко измерить на опыте, то формула имеет большое значение и позволяет вычислить силу тока в любой цепи.