Теории полимолекулярной адсорбции

В точке А изотерма, показанная на рис. 4.5, круто поднимается кверху, что указывает на то, что связывание адсорбтива с адсорбентом после образования молекулярного слоя не прекращается.

Для объяснения этого Поляни в 1915 г. предложил теорию полимолекулярпой адсорбции, называемую также потенциальной.

Основные положения теории Поляни:

1)адсорбция обусловлена чисто физическими силами;

2)на поверхности адсорбента нет активных центров, а адсорбционные силы действуют вблизи поверхности и образуют около этой поверхности непрерывное силовое поле;

3)адсорбционные силы действуют на сравнительно большие расстояния, превышающие размеры отдельных молекул адсорбтива и поэтому можно говорить о существовании у поверхности адсорбента адсорбционного объема, который заполняется молекулами адсорбтива;

4)действие адсорбционных сил по мере удаления от поверхности уменьшается и на некотором расстоянии становится равным нулю;

5)притяжение данной молекулы поверхностью адсорбента не зависит от наличия в адсорбционном пространстве других молекул;

6)адсорбционные силы не зависят от температуры и, следовательно, с изменением температуры адсорбционный объем не изменяется;

7)под воздействием адсорбционного поля возникает возможность образования нескольких слоев молекул адсорбата. Наибольшее притяжение и сжатие испытывает первый адсорбционный слой; газообразные продукты в нем конденсируются в жидкость. Притяжение последующих слоев снижается до тех пор, пока плотность вещества понизится до его плотности в окружающей среде.

Теория полимолекулярной адсорбции Поляни позволяет описать адсорбцию на пористых адсорбентах и каче­ственно объяснить характер S-образной изотермы. Однако эта теория не привела к выводу уравнения, описывающего эту изотерму.

Брунауэр, Эммет и Теллер разработали теорию применительно к адсорбции паров. Эта теория получила название теории БЭТ в соответствии с начальными буквами фамилий авторов.

Эта теория основана на следующих положениях:

1)на поверхности адсорбента имеется определенное число равноценных в энергетическом отношении активных центров;

2)каждая молекула первого слоя представляет собой активный центр для дальнейшей адсорбции, что приводит к образованию второго, третьего и т. д. слоев. При этом построение последующих слоев возможно при незаполненном первом;

3)взаимодействием соседних адсорбированных молекул в рамках одного слоя пренебрегают;

4)молекулы адсорбтива в последующих слоях по сумме статистических состояний подобны молекулам жидкости и отличаются от молекул первого слоя. Таким образом, адсорбированная фаза может быть представлена как совокупность адсорбционных комплексов – молекулярных цепочек, начинающихся молекулами первого слоя, непосредственно связанными с поверхностью адсорбента. При этом цепочки не взаимо­действуют между собой.

Схема полимолекулярной адсорбции по теории Бру-науэра, Эммета и Теллера представлена на рис. 4.6.

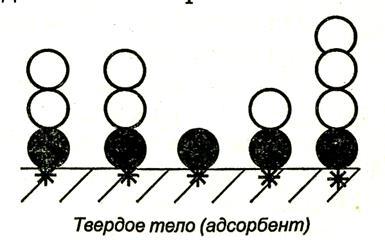
Рис. 4.6. Схема полимолекулярной адсорбции по теории БЕТ.

Итак, теория БЭТ исходит из наличия на поверхности адсорбента активных центров. В этом состоит ее сходство с теорией Ленгмюра. Вместе с тем, подобно теории Поляни, она допускает возможность образования нескольких адсорбционных слоев.

Авторы теории рассматривают адсорбцию как серию последовательных квазихимических реакций:

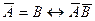К_р

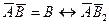К₁

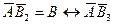К₂ и т. д.,

где А – активный центр, В – молекула адсорбтива, К_р, K₁, К₂ – константы соответствующих адсорбционных равновесий.

Авторы теории приняли, что во всех слоях, кроме пер1­вого, взаимодействуют между собой в основном молекулы адсорбата, как и при конденсации. Поэтому было принято, что:

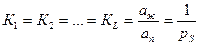
где K_L – константа конденсации пара, равная отношению активностей вещества в жидком состоянии а_ж и в состоянии насыщенного пара – а_n, принято а_ж = 1 (стандартное состояние), а а_n = p_S.

Брунауэр, Эммет и Теллер вывели следующее уравнение изотермы адсорбции паров:

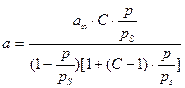(4.13)

В этом уравнении: p_S – давление насыщенного пара при данной температуре, р/p_S – относительное давление пара, С = К_р/K_L .

Уравнение (4.13) называется уравнением полимолекулярной адсорбции БЭТ.

При малых значениях р, далеких от p_S, т. е. при Р/P_S<<1, уравнение (4.13) превращается в уравнение мономолекулярной адсорбции Ленгмюра, а при дальнейшем уменьшении давления (р 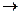0) переходит в закон Генри. По мере приближения р к p_S число свободных активных центров уменьшается и кратность комплексов растет. При р = p_s происходит объемная конденсация пара. Таким образом, уравнение БЭТ описывает всю S-образную изотерму адсорбции (см. рис. 4.5)/ Точка А на этой кривой отвечает завершению монослоя адсорбтива.

На теории БЭТ основан стандартный метод измерения удельной поверхности адсорбентов, катализаторов, порошков и других материалов. Для этого используется уравнение БЭТ в линейной форме:

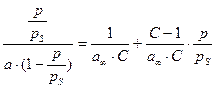(4.14)

По экспериментальным данным строят график в координатах 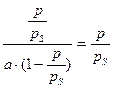(рис. 4.7). Тангенс угла наклона прямой к оси абсцисс равен 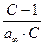, а отрезок, отсекаемый на оси ординат, – .

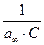Из графика находят 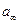, а затем рассчитывают удельную поверхность:

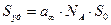, (4.15

где N_A – число Авогадро, S_o – площадь, занимаемая одной молекулой адсорбтива.

В качестве адсорбтива обычно используют газы (азот, аргон, криптон), в которых межмолекулярное взаимодействие на поверхности адсорбента является слабым, что соответствует исходным допущениям теории. Принимаются следующие значения S₀: азот – 0,162 нм², аргон – 0,138 нм², криптон – 0,195 нм².

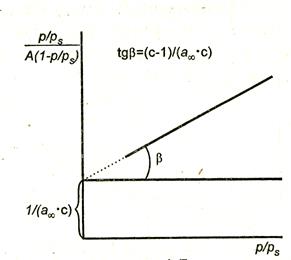
Рис.4.7. Изотерма полимолекулярной адсорбции в координатах линейной формы уравнения БЭТ

Необходимо отметить, что, несмотря на ряд недостатков, связанных с допущениями, которые лежат в основе теории БЭТ, она является весьма полезной теорией физической адсорбции.

КАПИЛЛЯРНАЯ КОНДЕНСАЦИЯ

Капиллярная конденсация – это процесс конденса­ции паров в порах твердого тела.

Это явление характерно для паров[4] веществ и обусловлено наличием у адсорбента мелких пор. В таких порах пары конденсируются при давлениях р, меньших, чем давление насыщенного пара, над плоской поверхностью жидкости при той же температуре – p_s, Это становится возможным при условии смачивания жидкостью стенок капилляра и образования вогнутых менисков (если образовавшаяся жидкость не смачивает поверхность, образуется выпуклый мениск, конденсация пара над которым происходит при давлении, большем давления пара над плоской поверхностью).

Количество удерживаемой капиллярными силами жидкости зависит от радиуса кривизны r поверхности раздела «жидкость–пар» согласно уравнению Кельвина (Томсона):

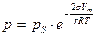, (4.15.)

где 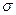– поверхностное натяжение жидкости, образующейся при конденсации пара, V_m – молярный объем этой жидкости, R – газовая постоянная, Т – температура.

Капиллярной конденсации предшествует адсорбция пара на поверхности конденсации. Капиллярная конденсация начинается при таком значении адсорбировавшегося вещества, при котором образуется мениск жидкости с радиусом кривизны г₀ более 2–3 диаметров молекулы.

Рис.4.8. Изотерма адсорбции, сопровождающейся капил­лярной конденсацией

Согласно уравнению Кельвина, при этом 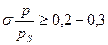для микропор (r₀ 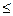1нм) уравнение Кельвина неприменимо.

В тех случаях, когда адсорбция осложнена капиллярной конденсацией, изотерма адсорбции отличается от приведенных ранее (см. рис. 4.1, 4.4 и 4.6) и имеет вид, представленный на рис. 4.8.

Капиллярную конденсацию используют для улавливания паров пористыми сорбентами. Большую роль она играет в процессах сушки, удерживания влаги почвами, строительными и другими материалами.