Термодинамика гальванического элемента без переноса

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Для изучения термодинамики химических реакций целесообразно использовать гальванический элемент без переноса, в котором реализуются обратимые электродные реакции, а измерение ЭДС электрохимической цепи осуществляют в условиях равновесия, т.е. в отсутствии поляризации электродов.

Определяя экспериментально ЭДС гальванического элемента и ее температурную зависимость, и используя термодинамические соотношения, можно рассчитать изменения свободной энергии Гиббса, энтропии и энтальпии для химической реакции, протекающей в гальваническом элементе, а также – среднюю активность и средний коэффициент активности электролита.

Гальванический элемент без переноса можно представить схемой

К | КА| А, (1)

где К и А – электроды, обратимые относительно катиона и аниона электролита КА, соответственно.

Если на электродах гальванического элемента установилось равновесие, то измерением ЭДС обратимого элемента можно определить изменение свободной энергии Гиббса (∆G) химической реакции, протекающей в элементе при постоянных температуре T и давлении p , по следующему уравнению

– ∆G = nFE , (2)

где n – количество электронов, участвующих в химической реакции;

F – постоянная Фарадея, Кл/(моль эквивалентов);

E – величина ЭДС, В.

Уравнение (2) показывает, что электрическая работа nFE, совершается гальваническим элементом за счет убыли свободной энергии Гиббса в результате протекания реакции.

В качестве конкретного примера рассмотрим электрохимическую цепь

Cu, Ag, AgCl| CuCl ₂ | Cu, (3)

в которой электролитом является раствор хлорида меди. Хлорид меди при растворении диссоциирует на ионы по реакции

CuCl₂ 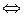Cu²⁺ + 2Cl^– . (4)

Правый электрод гальванического элемента обратим по катионам меди, а левый электрод обратим по хлорид-ионам.

На правом положительном электроде протекает реакция

Cu²⁺ + 2e 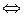Cu. (5)

и потенциал электрода 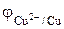описывается уравнением Нернста

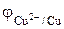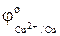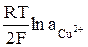= + , (6)

где 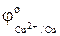– стандартное значение потенциала; 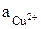– активность ионов меди в растворе электролита.

На левом отрицательном электроде протекает реакция

Ag + Cl^– – е 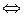AgСl. (7)

и потенциал электрода 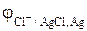описывается уравнением Нернста

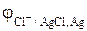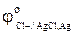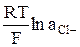= – , (8)

где 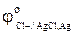– стандартное значение потенциала, В; 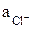– активность ионов хлора в растворе электролита.

Суммарную реакцию, протекающую в элементе, можно представить уравнением

2Ag + 2Cl^– + Cu²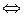⁺ Cu + 2AgСl. (9)

или в молекулярной форме

2Ag + CuCl₂ 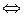Cu + 2AgСl. (10)

Выражение для ЭДС изучаемого элемента запишем в виде

Е= 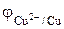– 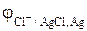= 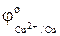+ 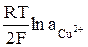– 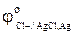+ 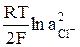(11)

или

Е = Е^о + 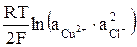, (12)

где Е^о = 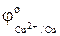– – 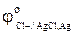стандартное значение ЭДС.

Согласно уравнению (4) и условию электронейтральности :

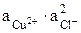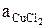= . (13)

Известно, что активность а_s соединения (соли) как целого можно представить уравнением

а_s = 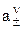= 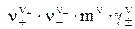, (14)

где: 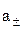– средняя активность электролита;

m – моляльная концентрация соли;

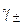– средний коэффициент активности;

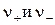– число катионов и анионов соответственно, которое образуется при растворении и диссоциации соли;

.

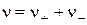В случае хлорида меди ν₊ = 1, ν_– = 2.

С учетом вышеизложенного, уравнение (12) можно записать в виде

Е = Е^о + 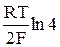+ 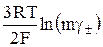, (15)

Стандартная величина ЭДС Е^о гальванического элемента (3) определяет константу равновесия реакции (9) К и связана с изменением стандартной энергии Гиббса в результате реакции ΔG^o уравнением

Е^о = 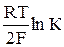= – 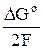. (16)

Из химической термодинамики известно, что

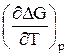= – ΔS и ΔG = ΔH – TΔS = ΔH + T 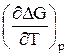. (17)

Тогда, согласно уравнениям (2) и (17)

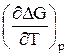– = ΔS = 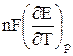, (18)

и ΔH = – nFE + nFT 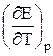, (19)

где ΔH и ΔS– изменения энтальпии и энтропии, соответственно, в результате реакции, протекающей в гальваническом элементе; 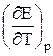– температурный коэффициент ЭДС.

Температурный коэффициент ЭДС элемента может быть равен нулю, больше нуля или меньше нуля.

Когда 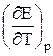= 0 из уравнений (2) и (19) следует, что

nFE = –ΔG = –ΔH. (20)

Если такой элемент будет работать в адиабатических условиях, то его температура не будет меняться.

В случае, когда 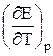< 0,

nFE = –ΔG < –ΔH (21)

и электрическая работа элемента меньше убыли энтальпии реакции. В адиабатических условиях температура в элементе будет повышаться.

Если 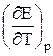>0, то

nFE = –ΔG > –ΔH, (22)

т.е. электрическая работа элемента больше изменения энтальпии при протекании реакции.

В этом случае в адиабатических условиях происходит понижение температуры гальванического элемента.

Таким образом, измерив ЭДС гальванического элемента при разных температурах, можно рассчитать ∆G, ∆S и ∆H реакции (9).

Используя справочные данные по стандартным значениям потенциалов медного 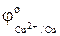и хлорсеребряного 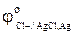электродов, которые при температуре 298К относительно водородного электрода сравнения равны 0,337 В и 0,222 В соответственно и уравнение (15), можно, рассчитать средний коэффициент активности электролита (CuCl₂ ).

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Целью работы является определение изменения термодинамических функций ΔG, ΔH, и ΔS в результате реакции, протекающей в гальваническом элементе (3), и среднего коэффициента активности γ_± электролита.

Порядок выполнения работы

1. Из безводной соли готовят растворы хлорида меди с концентрацией m 0,001; 0,004; 0,007 и 0,01 моляльности по 50 мл каждого.

2. Готовят к работе медный электрод аналогично тому, как описано в работе 1.

3. Готовят хлорсеребряный электрод. Для этого серебряную проволоку поляризуют анодно в растворе (0,75 – 0,8)N HCl при плотности тока 0,6 мА/см². Вторым электродом является платина. Процесс ведут до тех пор, пока серебряный электрод не приобретет коричневатый цвет. Следует избегать перехлорирования. Хлорированный электрод вымачивают в растворе (0,1– 0,2)N HCl. Обычно хлорсеребряный электрод готовится лаборантом заранее.

4. Собирают гальванический элемент (3), путем погружения в раствор хлорида меди, который предварительно заливают в электролизер, медного и хлорсеребряного электродов.

5.Подготовленный гальванический элемент помещают в термостат, в котором устанавливают температуру 298 К (m = 0,001).

6. После достижения указанной температуры элемент включают в измерительную цепь (см. рис.1 а,б).

Равновесную ЭДС определяют или компенсационным методом, подключая элемент к высокоомному потенциометру, или «прямым» измерением, подключая элемент к высокоомному цифровому вольтметру. Первый метод является более точным, поскольку во время измерения ток через гальванический элемент не течет, равновесие на электродах не нарушается и измеряется действительно равновесная ЭДС.

Компенсационным методом ЭДС измеряют в соответствии с инструкцией работы с потенциометром, «прямым» измерением ЭДС определяют в соответствии с инструкцией работы с высокоомным цифровым вольтметром. Инструкции предоставляет лаборант.

7. Измеряют ЭДС через каждые 10 минут, пока четыре последних измерения не покажут значения, совпадающие в пределах 1 мВ.

8. Повышают температуру до 308К и повторяют измерения ЭДС гальванической цепи указанным выше способом.

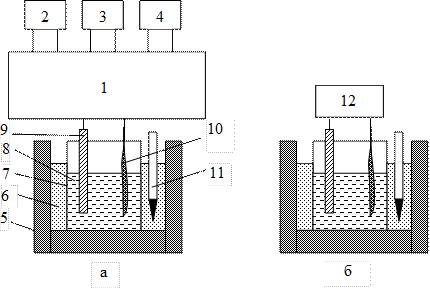Рис. 1. Схема цепи для измерения равновесной ЭДС. а – компенсационным методом; б – прямым измерением. 1 – высокоомный потенциометр; 2 – источник постоянного тока; 3 – нормальный элемент; 4 – нуль-гальванометр; 5 – термостат; 6 – жидкость термостата; 7 – электролизер; 8 – раствор хлорида меди; 9 – медный электрод; 10 – хлорсеребряный электрод; 11 – термометр; 12 – высокоомный вольтметр

9. Для определения концентрационной зависимости среднего коэффициента активности электролита выполняют измерения ЭДС гальванического элемента при 298 К для растворов хлорида меди с концентрациями 0,004; 0,007 и 0,01 моляльности.

Измеренные величины заносят в таблицы 1 и 2.

Таблица 1. Температурные зависимости (m = 0,001).

Температура, К	ЭДС, В	Температурный коэффициент ЭДС, мВ/К	∆G, кДж	∆S, Дж/К	∆H, кДж

Таблица 2. Концентрационные зависимости (Т = 298К).

Концентрация CuCl2, моль/кг	ЭДС, В		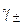I	hэксп	hтеор	∆G, кДж

Обработка результатов эксперимента.

Часть 1.

1. Считая зависимость ЭДС от температуры линейной функцией, рассчитывают температурный коэффициент ЭДС по уравнению

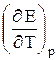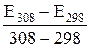= (23)

и заносят его в таблицу 1.

2. Используя уравнения (2), (18) и (19), рассчитывают изменение термодинамических функций ∆G, ∆S и ∆H в результате протекания реакции (9) и заносят их в таблицу 1.

Часть 2.

3. Используя значения стандартных потенциалов медного (0,337 В) и хлорсеребряного (0,222 В) электродов, по уравнению (14) рассчитывают значения 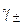для растворов указанных концентраций.

4. Рассчитывают ионную силу раствора и строят графическую зависимость в координатах lg 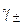= f ( ),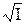

где I = 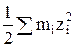– ионная сила раствора; m_i и z_i – моляльность и заряд i-го иона соответственно.

В интервале концентраций, в котором выполняется предельный закон Дебая-Хюккеля,

lg 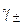= – |z₊·z_–|·h 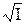, (23)

должна наблюдаться линейная зависимость между lg 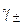и 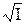. В уравнении (23) h – величина, включающая физические постоянные, свойства электролита и температуру и независящая от концентрации.

Её теоретическое значение равно

h_теор. = 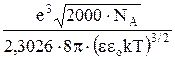= 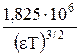, (24)

где е – элементарный заряд, Кл; N_A – число Авогадро, моль^–1; ε – относительная диэлектрическая проницаемость раствора; ε_о – электрическая постоянная, Ф/м. Коэффициент 1,825·10⁶ соответствует размерности h дм³/моль)^1/2.

5. В интервале концентраций, где выполняется уравнение (23), зависимость lg 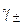= f ( 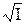) обрабатывают уравнением прямой линии и рассчитывают постоянную h_эксп в предельном законе Дебая – Хюккеля. Полученное значение h сравнивают с теоретическим h_теор.

6. По уравнению (2) определяют ∆G для заданных концентраций.

7. Рассчитанные величины заносят в таблицу 2.

8. На основании найденного значения 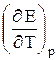делают вывод о характере изменения температуры гальванического элемента в адиабатических условиях.

По результатам работы делают выводы и вычисляют абсолютную и относительную ошибки.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Приведите примеры гальванических цепей без переноса.

2. Способы измерения ЭДС гальванических цепей. Расскажите их сущность.

3. В чем преимущества электрохимического способа изучения термодинамики химических реакций перед другими?

4. Изложите правила конструирования гальванической цепи без переноса.

5. Какие виды электродов существуют?

6. Уравнения Нернста для потенциалов электродов первого и второго рода.

7. Вывести уравнение (13).

8. Что означает термин «адиабатические условия»?

9. Написать реакции на электродах при замыкании гальванического элемента на нагрузку.

10. Что такое ионная сила раствора электролита? Рассчитать ионную силу раствора заданного преподавателем.

11. Показать направление электрического тока во внешней и внутренней цепях элемента при замыкании его на нагрузку.

12. Какие частицы переносят ток во внешней и внутренней цепях элемента при замыкании его на нагрузку? Направление движения частиц.

13. Вывести уравнение связи между активностью соединения a_s и средним коэффициентом активности электролита .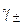

14. Написать основные уравнения связывающие термодинамические характеристики химической токообразующей реакции, протекающей в гальваническом элементе, и его электрические характеристики.

15. Объяснить влияние знака температурного коэффициента ЭДС на изменение температуры гальванического элемента в адиабатических условиях.

16. Предельный закон Дебая-Хюккеля.

17. Размерность величин в уравнениях.

РАБОТА 4