Самовільні процеси приводять систему до рівноваги

Наприклад, вирівнюється тиск, температура, концентрація тощо.

Друге начало термодинаміки визначає:

а) які процеси у відповідній системі при заданих умовах можуть відбуватися самовільно;

б) встановлює межу можливості самовільного протікання процесу, тобто стан рівноваги ;

в) дає можливість визначити, якими повинні бути зовнішні умови, щоб процес відбувався в певному напрямку.

Існує декілька формулювань ІІ закону термодинаміки:

· Теплота не може самочинно перейти від менш нагрітого тіла до більш нагрітого. (Р.Клаузіс. 1850р.)

· Неможливо здійснити процес, єдиним результатом якого було б перетворення теплоти в роботу. (Кельвін 1854р.)

· Вічний двигун другого роду неможливий. (Освальд 1888р.)

Під вічним двигуном другого роду розуміється періодично діюча теплова машина, яка здібна повністю перетворити теплоту в роботу, тобто без передачі частини її холодильнику.

· В ізольованій системі всі хімічні взаємодії між речовинами проходять тільки в тому напрямку, при якому система здійснює роботу під час якої зменшується вільна енергія, тобто тільки тої частинки енергії, яка здібна здійснити роботу.

Приклад 5.Як оцінюється можливість перебігу хімічного процесу ?

Відповідь:

Кожна система намагається перейти в стан з найменшим запасом енергії. Тому самовільний перебіг будь-якого процесу має супроводжуватися зменшенням внутрішньої енергії і ентальпії системи. Отже, від’ємне значення ентальпії ∆Н деякою мірою вказує на ймовірність перебігу хімічної реакції.

Для оцінки можливості перебігу хімічного процесу потрібно розглянути такі термодинамічні функції, як ентропія S і енергія Гіббса G.

Згідно з другим законом термодинаміки теплота, а отже, і внутрішня енергія не можуть повністю перетворюватися в роботу. При сталій температурі запас внутрішньої енергії можна подати у вигляді двох складових частин.

U = F + G

де F – корисна частина внутрішньої енергії, яка здатна виконувати роботу і називається вільною енергією;

G – непродуктивна частина внутрішньої енергії, яка не перетворюється на роботу і називається зв’язаною енергією.

У міру виконання системою роботи її вільна енергія зменшується, і, очевидно, чим більше система містить у собі вільної енергії, тим більшу роботу вона може виконувати. Характеристикою зв’язаної енергії є ентропія S(від грец.
en – всередину, trope – звертати).

Щоб охарактеризувати ентропію, розглянемо приклад. Є посудина, яка поділена перегородкою. В одній частині посудини є газ, а в другій – вакуум (стан І). Якщо перегородку прибрати, газ буде дифундувати у вакуум, його молекули рівномірно розподіляться по всьому об’єму посудини
(стан ІІ). Відбувся самовільний (спонтанний) процес розподілу молекул по всьому об’єму системи. Зворотній процес самочинного стискання газу – неможливий.

Розглянуте явище розширення газу вказує на направленість процесу до найбільш ймовірного стану, тобто до стану, якому відповідає максимальна безладність розподілу частинок. При цьому енергія, маса і загальний об’єм системи залишилися сталими, а змінився лише ступінь безладності: в стані 1 система мала більший ступінь порядку, бо концентрація газу вища, міжмолекулярні віддалі меші, отже, й міжмолекулярні зв’язки сильніші, що зумовлює більшу фіксованість молекул відносно одна одної.

Для оцінки ступеня безладності системи вводять функцію стану системи, яку називають ентропією.

Це поняття прийшло в науку з теорії теплових машин, тепер воно повністю переосмислено статистичною фізикою і вводиться як міра невпорядкованості систем, що складаються з великої кількості частинок. У такому вигляді воно набуло великого значення для хімічних і біологічних процесів.

Вводячи 1865 році поняття ентропії, Р. Клаузіус мав на увазі дослідити функцію стану, зміна якої показуватиме напрям фізичних і хімічних процесів в ізольованих системах. Щоб розкрити зміст цієї функції скористаємось статистичним підходом Л.Больцмана і М.Смолуховського.

Уявимо велику сукупність чатинок. Макростан такої системи можна описати, використавши такі функції стану, як температура, тиск, об’єм. Цю саму систему можна описати також через миттєві характеристики кожної частинки системи, її положення в просторі, швидкість і напрям переміщення. Оскільки мікростани змінюються безперервно, то певному макростану відповідає велика кількість мікростанів. Число останніх за допомогою яких реалізується такий макростан, називається термодинамічною ймовірністю системи (W). Больцман встановив, що функція стану ентропія пов’язана з термодинамічною ймовірністю системи:

S=(R/N_А)lnW

де, R – універсальна газова стала; N_А – число Авогадро.

Якщо віднести величину ентропії до моль речовини для цього вираз треба помножити на N_А, тоді ентропія вимірюється в таких самих одиницях, як і R, вони називаються ентропійними одиницями (е.о.).

На відміну від ентальпії абсолютні значення ентропії можна визначити експериментально. Для цього необхідно знати величину W.

Зміна ентропії переходу речовин з початкового стану в кінцевий виражається рівнянням.

∆S = Sкінц. – Sвих. = Rln(Wкінц./Wвих.)

Зміна ентропії проходить під час різних процесів.

Фазові переходи

Під час плавлення твердої речовини, випаровуванні рідини і сублімації неупорядкованість в системі збільшується, а значить зростає ентропія. Будь-який фазовий перехід зв’язаний із певним постійним тепловим ефектом (теплота плавлення, теплота випаровування тощо), можна назвати тепловою фазою переходів (∆H ф.п.). Ці переходи відбуваються при постійній температурі, тобто є ізотермічні. Значить для фазових переходів одного моля речовини справедливе рівняння

∆S ф.п.= (∆H ф.п.)/Тф.п.

Приклад 1.

Обчисліть зміну стандартної ентропії системи в результаті випаровування 100г води.

З табличних даних берем значення ∆H⁰_вип.Н₂О
і Т_кип. Н₂О і підставимо в формулу: S⁰=100/18·(41,09·103)/373,2=611,68 кДж/К

Зміна температури

Нагрівання речовин супроводжується збільшенням, а охолодження - зменшенням ентропії. Для ізобарного процесу:

Q=C_p·dT

Якщо взяти середнє значення теплоємності, то

∆S = 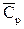·lnT₂/T₁

Приклад 2.

Обчисліть зміну ентропії 2 моль аміаку при нагріванні від 400 до 500 К.

З табличних даних беремо середню теплоємність газоподібного аміаку:

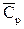= 8,52 Дж·моль^-1·К^-1

Тоді:

∆S = 2·8,52·ln(500/400) = 3,80 Дж·К^-1

Хімічні реакції

Ентропія 1 моль речовини в його стандартному стані при відповідній температурі називається стандартною ентропією S⁰.(стандартні ентропії багатьох простих і складних речовин даються в довідникових таблицях). Слід зазначити, що стандартні ентропії простих речовин не дорівнюють 0. Зміна стандартної ентропії під час хімічних реакції може бути обчислена згідно рівняння:

∆S⁰=∑ S⁰_прод.- ∑ S⁰_{вих.реч.}

При сумуванні абсолютних ентропій кожна із них повинна бути помножена на відповідний стехіометричний коефіцієнт.

Приклад 3.

Обчисліть зміну стандартної ентропії в реакції синтезу амоніаку:

N₂+3H₂=2NH₃

З довідкової літератури знаходимо значення стандартних абсолютних ентропій:

S⁰ (NH_3(г)) = 193 Дж·моль^-1К^-1

S⁰ (N_2(г)) = - 192 Дж·моль^-1К^-1

S⁰ (H_2(г)) = 131 Дж·моль^-1К^-1

S⁰=2·193-192-3·131=-195 Дж·моль^-1К^-1

В даному випадку ентропія зменшиться, оскільки в результаті реакції зменшиться об’єм газоподібних речовин, а значить і невпорядкованість в системі.

Введення стандартних ентропій дає змогу встановити такі закономірності:

1. Ентропія простих речовин і сполук елементів – це періодична властивість.

2. У межах даної підгрупи елементів періодичної системи ентропія простих речовин зростає.

3. Чим більша твердість речовин, тим менша її ентропія.

4. Ентропія речовин, що перебувають в аморфному або склоподібному стані більша, ніж кристалічних речовин.

5. Ускладення молекул зумовлює зростання ентропії. Наприклад:

S⁰₂₉₈ (О) =161 Дж/моль

S⁰₂₉₈ (О₂) =205 Дж/моль

S⁰₂₉₈ (О₃) =239 Дж/моль

Приклад 6. Сформулюйте основні закони термохімії. Як проводиться термохімічні розрахунки ? Поясніть на прикладах.

Відповідь:

Визначення теплових ефектів різних хімічних реакцій грунтуються на двох основних законах термохімії .

Перший закон термохімії встановили французькі вчені А.Лавуазьє і П. Лаплас наприкінці XVIII ст.: