Расчетные формулы по электротехнике
| Формулы | Обозначение и единицы измерения | |||||||||||||||||||||||
| Закон Ома для участка цепи постоянного тока | ||||||||||||||||||||||||
| 1. Напряжение на участке цепи, В U=ІR | I - сила тока на этом участке, А; R - сопротивление участке цепи, Ом; U - напряжение на участке цепи, В; | |||||||||||||||||||||||
| 2. Ток на участке цепи, А I=U/R | ||||||||||||||||||||||||
| 3. Сопротивление на участке цепи, Ом R=U/I | ||||||||||||||||||||||||
4. Сопротивление проводника постоянному току, Ом R0=ρ 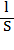 | ρ - удельное сопротивление, 10-6Ом∙м; l - длина, м; S - сечение, мм2; | |||||||||||||||||||||||
| 5. Зависимость активного сопротивления проводника от температуры R=R1∙[1+α∙(t-t1)] | R, R1 - сопротивления проводника соответственно при температурах t и t1, 0С, Ом; α -температурный коэффициент, 1/0С; | |||||||||||||||||||||||
| 6. Общее сопротивление электрической цепи при последовательном соединении сопротивлений R=R1+R2+R3+…+Rn | R - общее сопротивление цепи, Ом; R1 ,R2 ,R3…Rn - сопротивления n резисторов, Ом; | |||||||||||||||||||||||
| 7. Сопротивление цепи из двух параллельных резисторов R=R1∙R2/R1+R2 | ||||||||||||||||||||||||
8. Сопротивление цепи из n параллельных резисторов | ||||||||||||||||||||||||
| 9. Общая емкость конденсаторов
| С - общая емкость конденсаторов, Гн; С1,С2,С3… Сn - емкость отдельных конденсаторов цепи, Гн; | |||||||||||||||||||||||
| 10. Мощность постоянного тока, Вт P=UI=I2R=U2/R | I - сила тока в цепи, А; U - напряжение в цепи, В; R - сопротивление, Ом; | |||||||||||||||||||||||
| 11. Энергия электрической цепи, Дж W=Pt | P - мощность в цепи, Вт; t - время, с; | |||||||||||||||||||||||
| 12. Тепловой эффект A=0,24∙I2∙R∙t= 0,24∙U∙I∙t | A - количество выделяемого тепла, кал; t - время протекания тока; R - сопротивление, Ом; | |||||||||||||||||||||||
| Закон Ома при переменном токе | ||||||||||||||||||||||||
| 13. Ток, А I=U/Z | I - ток, А; U - напряжение, В; Z - полное сопротивление в цепи, Ом; - индуктивное сопротивление цепи, Ом; Z= 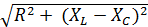 = = 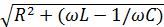 XL=ωL – индуктивное сопротивление цепи, Ом XC=1/ωC – емкостное сопротивление цепи, Ом ω - угловая частота сети, с-1; f - частота переменного тока, Гц; L - индуктивность, Гн; C - емкость, Ф; XL=ωL – индуктивное сопротивление цепи, Ом XC=1/ωC – емкостное сопротивление цепи, Ом ω - угловая частота сети, с-1; f - частота переменного тока, Гц; L - индуктивность, Гн; C - емкость, Ф; | |||||||||||||||||||||||
| 14. Напряжение, Вт U=I∙Z | ||||||||||||||||||||||||
15. Закон Кирхгофа для узла (1-й закон): 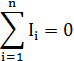 для замкнутого контура (2-й закон): E= для замкнутого контура (2-й закон): E= 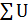 = = 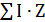 | Ii- токи в отдельных ветвях цепи, сходящихся в одной точке, А i=(1,2,3,…); E - ЭДС, действующая в контуре, В; U - напряжение на участке контура, В; Z - полное сопротивление участка, Ом; | |||||||||||||||||||||||
| 16. Распределение тока в двух параллельных ветвях цепи переменного тока I1/I2 = Z2/Z1 | I1 - ток первой цепи, А; I2 - ток второй цепи, А; Z1 - сопротивление первой ветви, Ом; Z2 - сопротивление второй ветви, Ом; | |||||||||||||||||||||||
17. Полное сопротивление, Ом Z= 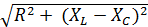 | R - активное сопротивление, Ом; XL- индуктивное сопротивление, Ом; XC - емкостное сопротивление, Ом; | |||||||||||||||||||||||
18. Реактивное (индуктивное) сопротивление, Ом XL=ωL=2 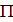 ∙f∙L ∙f∙L | ω- угловая частота, рад/с; f - частота колебаний, Гц; L - индуктивность, Гн; C - емкость, Ф; X - полное реактивное сопротивление, Ом; | |||||||||||||||||||||||
19. Реактивное (емкостное) сопротивление, Ом XC=1/ωL= 1/2 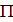 ∙f∙L ∙f∙L | ||||||||||||||||||||||||
| 20. Полное реактивное сопротивление X= XL- XC | ||||||||||||||||||||||||
21. Индуктивность катушки, Гн без стального сердечника: L= 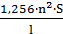 10-8 со стальным сердечником: L= μ 10-8 со стальным сердечником: L= μ 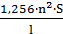 10-8 10-8 | n- число витков катушки; S - площадь среднего сечения обмотки, составляющей катушку, см2; l - длина катушки, см; μ - магнитная проницаемость материала сердечника, Гн/м; | |||||||||||||||||||||||
| 22. Закон электромагнитной индукции для синусоидального тока E= 4,44∙f∙ω∙B∙S∙10-4 | E - наведенная ЭДС, В; f - частота, Гц; ω- число витков обмотки; B -индукция магнитная, Тл; S - сечение магнитопровода, см2; | |||||||||||||||||||||||
23. Электродинамический эффект тока для двух параллельно расположенных проводников F=Im1 ∙Im2∙  ∙10-7 ∙10-7 | F - сила, действующая на проводниках, Н; Im1, Im2 - амплитудные значения токов в параллельных проводниках, А; l - длина проводника, см; α - расстояние между проводниками, см; | |||||||||||||||||||||||
24. Зависимости для цепи переменного тока ток в цепи: I= 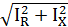 IR=I∙cosω IX=I∙ sinω напряжение в цепи: U= IR=I∙cosω IX=I∙ sinω напряжение в цепи: U= 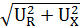 UR=U∙ cosω UX=U∙ sinω UR=U∙ cosω UX=U∙ sinω | I - ток в цепи, А; IR- активная составляющая тока, А; IX- реактивная составляющая тока, А; U - напряжение в цепи, В; UR- активная составляющая напряжения, В; UX- реактивная составляющая напряжения, В; | |||||||||||||||||||||||
| 25. Соотношение токов и напряжений в трехфазной системе а) соединение «звезда»: IЛ=IФ, UЛ=1,73∙UФ; б) соединение «треугольник»: UЛ= UФ, IЛ=1,73∙IФ; | IЛ - ток линейный, А; IФ - ток фазный, А; UЛ - напряжение линейной, В; UФ - напряжение фазное, В; | |||||||||||||||||||||||
26. Коэффициент мощности cos 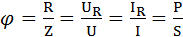 | P - реактивная мощность, Вт; S - полная мощность, В∙А; R - активное сопротивление, Ом; Z - полное сопротивление, Ом; | |||||||||||||||||||||||
27. Мощность и энергия тока в цепи переменного тока а) цепь однофазного тока: P=I∙U∙ cos 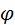 , Q=I∙U∙sin , Q=I∙U∙sin 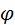 , S=IU= , S=IU= 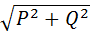 ; WR=I∙U∙ cos ; WR=I∙U∙ cos 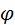 ∙t; WX= I∙U∙sin ∙t; WX= I∙U∙sin 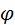 ∙t; б) цепь трехфазного тока: P= ∙t; б) цепь трехфазного тока: P= 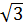 ∙I∙U∙ cos ∙I∙U∙ cos 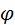 ; Q= ; Q= 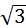 ∙I∙U∙sin ∙I∙U∙sin 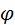 ; WR= ; WR= 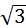 ∙I∙U∙ cos ∙I∙U∙ cos 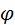 ∙t; WX= ∙t; WX= 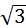 ∙I∙U∙sin ∙I∙U∙sin 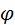 ∙t; ∙t; | Q - реактивная мощность, вар; WR - активная энергия, Вт∙ч; WX - реактивная энергия, вар∙ч; t - время протекания тока, ч; S - полная мощность, В∙А; | |||||||||||||||||||||||
28. Реактивная мощность конденсатора, Вар QC=U2∙ω∙C=U2∙2П∙f∙C, где конденсатора, Ф С= 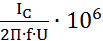 | IC- ток, протекающий через конденсатор, А; U - напряжение, приложенное к конденсатору, В; | |||||||||||||||||||||||
29. Синхронная частота вращения электрической машины, об./мин n= 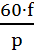 | f - частота питающей сети, Гц; p - число пар полюсов машины; | |||||||||||||||||||||||
30. Вращающий момент электрической машины, Н∙м M=9,555∙  | P - мощность, Вт; n - частота вращения, об./мин; |
Приложение 13
Расчёт сложных электрических цепей
В сложных электрических цепях может содержаться несколько замкнутых контуров с любым размещением в них источников энергии и потребителей. Поэтому такие сложные цепи нельзя свести к сочетанию последовательных и параллельных соединений.
Используя законы Ома и Кирхгофа, можно найти распределение токов и напряжений на всех участках любой сложной цепи.
Одним из методов расчёта сложных электрических цепей является метод наложение токов, сущность которого заключается в том, что ток в какой-либо ветви представляет собой алгебраическую сумму токов, создаваемых в ней каждой из ЭДС цепи в отдельности. На рис. изображена цепь, содержащая три источника с ЭДС E1, E2, E3и четыре последовательно соединенных резистора R1, R2, R3, R4. Если пренебречь внутренним сопротивлением источников энергии, то общее сопротивление цепи R=R1+R2+R3+R4. Допустим сначала, что ЭДС первого источника E1 ≠0, а второго и третьего E2 = 0 и E3 = 0. Затем положим E2 ≠ 0, а E1 = 0 и E3 = 0. И наконец, полагаем E3≠ 0, а E1 = 0 и E2 = 0. В первом случаи ток в цепи, совпадающий по направлению с ЭДС E1, равен I1 = E1/R; во втором случаи ток в цепи, совпадающий по направлению с ЭДС E2, равен I2 = E2/R; в третьем случаи ток равен I3 = E3/Rи совпадает по направлению с ЭДС E3. Так как ЭДС E1 и E3 совпадает по направлению в контуре, то и токи I1 и I3 также совпадают, а ток I2 имеет противоположное направление, так как ЭДС E2 направлена встречно по отношению к ЭДС E1 и E3. Следовательно, ток в цеп равен
I = I1 – I2 + I3 = E1 / R – E2 / R + E3 / R =
= (E1 – E2 + E3) / (R1 + R2 + R3).
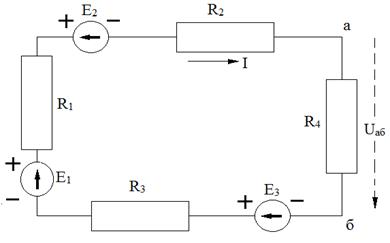
Электрическая цепь с тремя источниками энергии
Направление на любом участке цепи, например между точками а и б,равно Uаб = IR4.
При расчёте сложных цепей для определения токов во всех ветвях цепи необходимо знать сопротивления ветвей, а также значение и направление всех ЭДС.
Перед составлением уравнений по законам Кирхгофа следует произвольно задаться направлениями токов в ветвях, показав их на схеме стрелками. Если действительное направления тока в какой-либо ветви противоположно выбранному, то после решения уравнений этот ток получится со знаком « - ». Число необходимых уравнений равно числу неизвестных токов, причём число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов цепи; остальные уравнения составляются по второму закону Кирхгофа, причем следует выбрать наиболее простые контуры и так, чтобы каждый из них содержал хотя бы одну ветвь, не входившую в ранее составленные уравнения.
Расчет сложной цепи с применением уравнений по законам Кирхгофа рассмотрим на примере двух параллельно включенных источников, замкнутых на сопротивление. Пусть ЭДС источников E1 = E2 =120B, их внутренние сопротивления R1 = 3 Ом и R2 = 6 Ом, сопротивление нагрузки R = 18 Ом.
Так как число неизвестных токов 3, то необходимо составить три уравнения. При двух узловых точках необходимо одно узловое уравнение по первому закону Кирхгофа: I = I1 + I2. Второе уравнение запишем при обходе контура, состоящего из первого источника и сопротивление нагрузки: E1 = I1R1 + IR. Аналогично запишем третье уравнение: E2 = I2R2 + IR. Подставляя числовые значения, получим 120 В = 3I1 + 18I и 120 В = 6I2 + 18I. ТаккакE1 – E2 = I1R1 – I2R2 = 3I1 – 6I2 = 0, тоI1 = 2I2иI = 3I2. Подставляя эти значения в выражение для ЭДС E1, получим 120 =
= 2I2 ×3 + 18 × 3I2 = 60I2, откуда I2 = 120 / 60 = 2A, I1 = 2I2 = 4A, I = I1++I2 = 6A.
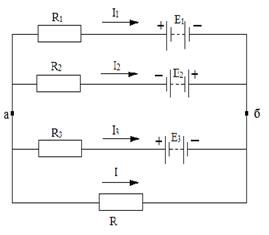
В сложных электрических цепях, имеющих две узловые точки а и б и состоящих из нескольких параллельно соединенных источников энергии, работающих на общий приемник, удобно использовать метод узловых напряжений. Обозначив потенциалы в узловых точках φа – φб, напряжение между этими точками U можно выразить разностью этих потенциалов, т.е.
U = φа – φб.
 а
а 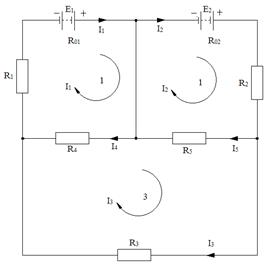 б
б
Схема к расчету сложно электрической цепи:
а – по методу узловых напряжений;
б – по методу контурных токов
Приняв за положительное направление ЭДС и токов в ветвях от узла, а к узлу б для каждой из ветвей, можно записать равенства: I1 = ( φа – φб – E1)/
/ R1 = ( U – E1)g1; I2 = ( φа – φб – E2) / R2 = ( U – E2)g2; I3 = ( φа – φб – E3) / / R3 = ( U – E3)g3; I = ( φа – φб ) / R = Ug.
На основании первого закона Кирхгофа для узловой точки имеем I1 + I2 + + I3 +I = 0. Подставим в эту сумму значения токов, найдем
( U – E1 )g1 + ( U + E2)g2 + ( U – E3)g3 + Ug = 0,
откуда
U = ( E1g1 – E2g2 + E3g3) / (g1 + g2 + g3 + g) =
= Σ Eg / Σ g,
т.е. узловое напряжение равно алгебраической сумме произведений ЭДС и проводимостей всех параллельных ветвей, деленной на сумму проводимостей всех ветвей. Вычислив по этой формуле узловое напряжение и воспользовавшись выражениями для оков в ветвях, легко определить эти токи.
Для определения токов в сложных цепях, содержащих несколько узловых точек и ЭДС, применяют метод контурных токов. Который дает возможность сократить число уравнений, подлежащих решению. Предполагают, что в ветвях, входящих в состав двух смежных контуров, протекают два контурных тока, первый из которых представляет собой ток одного из смежных контуров, а второй – другого контура. Действительный ток в рассматриваемом участке цепи определяется суммой или разностью этих двух токов в зависимости от взаимного относительного направления.
При использовании метода контурных токов составляют уравнения, исходя из суммы сопротивлений, входящих в состав данного контура, и суммы сопротивлений, входящих в состав ветви, общей для смежных контуров. Первую сумму условно обозначают двойным индексом, например R11, R22 и т.д., а вторую – индексом, содержащим номера контуров, для которых данный участок цепи является общим, например R12, R13 и т.д.
Если контур содержит несколько источников с ЭДС E1, E2, E3 и т.д., то на основании второго закона Кирхгофа для этого контура можно записать следующее уравнение: E1 ± E2 ± E3 + … = I1R11 + I2R12 + I3R13 +… . В этом уравнении знак «+» или « - » берется в зависимости от взаимного относительного направления ЭДС и токов в контуре ( при одинаковом направлении - «+», в противоположном - « - » ). Аналогичные уравнения могут быть записаны для всех контуров, входящих в сложную электрическую цепь. Таким образом, алгебраическая сумма ЭДС каждого контура равна алгебраической сумме произведения тока в данном контуре на сумму сопротивлений всех звеньев, образующих его, и контурных токов всех контуров, смежных с данным контуром, на сопротивления общих звеньев.
На рис. б изображена сложная электрическая цепь, содержащая три контура. В цепи два источника с ЭДС E1= 12 B, E2 = 8 B и внутренними сопротивлениями R01 = 4 Ом, R02 = 3 Ом и пять сопротивлений
R1 = 20 Ом, R2 = 29 Ом, R3 = 40 Ом, R4 = 8 Ом, R5 = 16 Ом.
Находим сопротивления: R11 = R1 + R01 + R13 = 20 + 4 + 8 = 32 Ом;
R22 = R2 + R02 + R23 = 29 + 3 + 16 = 48Ом; R33 = R3 + R31 + R32 =
= 40 + 8 + 16 = 64 Ом; R13 = R31 = 8 Ом; R23 = R32 = 16 Ом.
На основании второго закона Кирхгофа составляем уравнения:
для контура 1:
E1 = I1R11 – I3R13; 12 = 32I1 – 8I3;
для контура 2:
E2 = I2R22 – I3R23; 8 = 48I2 – 16I3;
для контура 3:
E3 = I3R33 – I3R32; 0 = 64I3 – 16I2 – 8I.
Решаяэтиуравнения, находим: I1 = 0,4A; I2 = 0,2A; I3 = 0,1A; I4 = I1 – - I3 = 0,3A; I5 = I2 – I3 = 0,1A.
Приложение 14
