Где f - фрикционный коэффициент , v – скорость движения молекулы.

Фрикционный коэффициент макромолекул зависит от их формы и размеров. Для молекул сферической формы (например, для глобулярных белков, ) f = 6 ηπr

Тогда, сила сопротивления при дфижении сферических макромолекл в жидкости выражается законом Стокса

F = - 6 ηπr v

На поведение макромолекул в растворе основное влияние оказывают столкновение с молекулами растворителя. Подсчитано, молекула белка средних размеров в разбавленном растворе испытывает 10¹³ - 10¹⁵ столкновений в секунду, обусловленные тепловыми движениями. Это определяет статистическое поведение макромолекул- хаотичность движения (броуновское движение).

Согласно законам статистической физики, параметром, описывающим хаотическое движение молекул, является среднеквадратичное смещение х־²

х־² = 2 К₀ТΔ t/ f

где – время наблюдения за хаотическим движением макромолекул. Таким образом, измерив х־² можно определить значение f,следовательно, и размеры макромолекулы. Однако, невозможно следить за поведением отдельной молекулы, и следовательно, невозможно прямо определить значениех־².Поэтому определение значений х־^{2 и} f проводят косвенными способами. Один из таких способов – это определение коэффициента диффузии D. Диффузия – это самопроизвольное перемещение молекул из области с высокой концентрацией в область с низкой концентрацией в результате хаотического движения. Поток вещества ( количество молекул в единицу времени) при поступательной диффузии описывается первым законом Фика:

dn/dt = - DAdc/dx,

где n – число молекул; А – площадь перемещения; с – концентрация вещества; D - коэффициент диффузии (м² с^-1). Знак минус означает, что поток направлен в сторону уменьшения концентрации вещества.

Коэффициент диффузии связан с х־² и f следующей формулой :

D = х־² / 2 Δ t = К₀Т/ f

Таким образом, измерив D можно вычислить значение f и, соответственно, можно сделать заключение о форме макромолекулы.

Для сферических макромолекул радиусом r f = 6 ηπr = К₀Т/ D,

тогдаr = К₀Т/ 6 ηπ D.

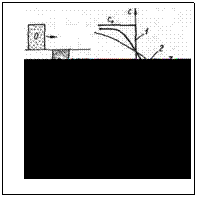
Рис. 5. Измерение коэффициента диффузии макромолекул:

a - диффузия макромолекул на границе раздела раствор-растворитель; б - изменение во времени концентрации (с) макромолекул и градиента концентраций 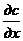границе раздела раствор–растворитель; 1 – t = 0; 2 – t₂; 3– t₂; H – высота пика

Отсюда следует, что для сферических макромолекул молекулярная масса обратно пропорциональна коэффициенту диффузии в кубе:

М ~1/D³

Величину Dможно определить экспериментально. Для этого растворитель наслаивают на концентрированный раствор макромолекул и измеряют размывание границы между растворителем и раствором. Размывание границы можно регистрировать оптическими методами: по измерению оптической плотности в УФ- области; по измерению показателя преломления растворов.

Таблица 1

Зависимость физических параметров от молекулярной массы белков (константа седиментации 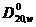, коэффициент диффузии 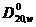, парциальный удельный объем V и молекулярная масса М

Белок	S0 1013, с	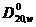1011, м2 ·с-1	V, л·кг-1	М, кДа
Цитохром с1	1,71	11,40	0,728	13,3
Лизоцим	1,91	11,20	0,703	13,9
Рибонуклеаза	2,00	13,10	0,707	12,6
Миоглобин	2,04	11,3	0,74	16,9
Сывороточный альбумин	4,60	6,10	0,733	68,45
Каталаза печени	11,2	4,10	0,735	250,0
Уреаза	18,6	3,46	0,73	480,0
Гемоцианин	98,9	1,38	0,738	6,6·103

Установленную экспериментальным путем величину коэффициента диффузии обычно приводят к стандартным условиям (бесконечное разбавление в воде w, при 293 К) По формуле

= .

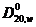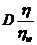В таблице 1 приведены некоторые физические параметры ряда белков с разными молекулярными массами, с различными формами и размерами молекул. Как видно из таблицы, соотношение М ~1/D³, полученный для сферических макромолекул не всегда выполняется. Например, при увеличении молекулярной массы белка в 450 раз (сравниваем гемоцианин с цитохромом с₁) коэффициент диффузии уменьшается всего в 9 раз. Это свидетельствует о том, что коэффициент Dзависит не только от массы молекул, но и от их формы.