Колебательные процессы в биологии. Значение их теоретического исследования. Предельные циклы и тд.

Для биологических систем характерно периодическое изменение различных характеристик. Период этих колебаний может быть связан с периодическими изменениями условий жизни на Земле - смена времен года, смена дня и ночи. Существуют и другие геофизические ритмы –солнечные, лунные, связанные с периодами атмосферных явлений. Геофизические и биологические ритмы сопоставлены на рис. 8.1. Но многие периодические процессы имеют частоту изменения, не связанную очевидным образом с внешними геокосмическими циклами. Это так называемые «биологические часы» различной природы, начиная от колебаний биомакромолекул, биохимических колебаний, вплоть до популяционных волн.

Внутриклеточные колебания задают эндогенные биологические ритмы, которые свойственны всем живым системам. Именно они определяют периодичность деления клеток, отмеряют время рождения и смерти живых организмов. Модели колебательных систем используются в ферментативном катализе, теории иммунитета, в теории трансмембранного ионного переноса, микробиологии и биотехнологии.

С некоторыми из типов периодических движений мы уже имели дело при рассмотрении особых точек типа центр и затухающих или нарастающих колебаний в случае устойчивого и неустойчивого фокуса. Однако «биологические часы» имеют свойство, отличающее их от рассмотренных типов колебаний - неизменность во времени периода и амплитуды таких колебаний, означающую стационарность и устойчивость колебательного режима.

Если колебания в системе имеют постоянные период и амплитуду, устанавливаются независимо от начальных условий и поддерживаются благодаря свойствам самой системы, а не вследствие воздействия периодической силы, система называется автоколебательной.

Незатухающие колебания в таких системах устойчивы, так как отклонения от стационарного колебательного режима затухают. К классу автоколебательных систем относятся колебания в гликолизе и других метаболических системах, периодические процессы фотосинтеза, колебания концентрации кальция в клетке, колебания численности животных в популяциях и сообществах.

Предельный цикл.В фазовом пространстве такому типу поведения соответствует притягивающее множество (аттрактор), называемое предельным циклом.

Предельный цикл.В фазовом пространстве такому типу поведения соответствует притягивающее множество (аттрактор), называемое предельным циклом.

Предельный цикл есть изолированная замкнутая кривая на фазовой плоскости, к которой в пределе при t ® ¥ стремятся все интегральные кривые. Предельный цикл представляет стационарный режим с определенной амплитудой, не зависящий от начальных условий, а определяющийся только организацией системы. Существование предельного цикла на фазовой плоскости есть основной признак автоколебательной системы. Очевидно, что при автоколебательном процессе фаза колебаний может быть любой.

Остановимся на общих характеристиках автоколебательных систем. Рассмотрим систему уравнений общего вида:

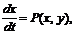
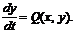
Если T (T > 0) — наименьшее число, для которого при всяком t

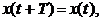
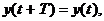
то изменение переменных x = x(t), y = y(t) называется периодическим изменением с периодом T.

Периодическому изменению соответствует замкнутая траектория на фазовой плоскости, и обратно: всякой замкнутой траектории соответствует бесконечное множество периодических изменений, отличающихся друг от друга выбором начала отсчета времени.

Если периодическому изменению на фазовой плоскости соответствуетизолированная замкнутая кривая, к которой с внешней и внутренней стороны приближаются (при возрастании t) соседние траектории по спиралям, эта изолированная замкнутая траектория есть предельный цикл.

Простые примеры позволяют убедиться, что система общего вида (8.1) допускает в качестве траекторий предельные циклы.

Например, для системы

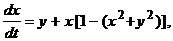
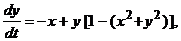
траектория 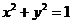является предельным циклом. Его параметрические уравнения будут:

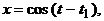
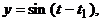
а уравнения всех других фазовых траекторий запишутся в виде:

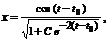
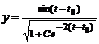
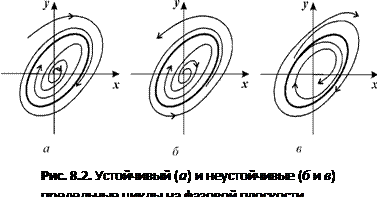
Предельный цикл называетсяустойчивым, если существует такая область на фазовой плоскости, содержащая этот предельныйцикл, - окрестность e, что все фазовые траектории, начинающиеся в окрестности e, асимптотически при t ® ¥ приближаются кпредельному циклу.

Если же, наоборот, в любой сколь угодно малой окрестности e предельного цикла существует по крайней мере одна фазовая траектория, не приближающаяся к предельному циклупри t ® ¥, то такой предельный цикл называется неустойчивым. Такие циклы разделяют области влияния (бассейны) разных притягивающих множеств.

На рис. 8.2 изображены устойчивый предельный цикл (а) и неустойчивые (б) и (в). Неустойчивые предельные циклы, подобные изображенному на рис. 8.2 б, такие, что все траектории с одной стороны (например, изнутри) приближаются к ним, а с другой стороны (например, извне) удаляются от них при t ® ¥, называют «полуустойчивыми» или двойными. Последнее название связано с тем, что обычно такие циклы при подходящем изменении параметра системы расщепляются на два, один из которых устойчив, а другой неустойчив.