Закон сохранения импульса реактивное движение.

Закон сохранения импульса.

До взаимодействия

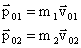
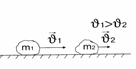
После взаимодействия

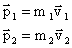
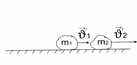
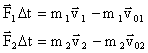
Согласно 3 з-ну Ньютона: 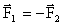, следовательно:

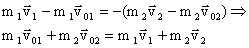
Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.

Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы).

В общем виде: т.к. система замкнутая, то 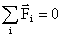, следовательно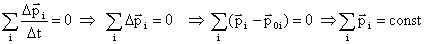

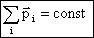
Билет №9

Работа и мощность.

При перемещении тела под действием силы совершается работа. Следовательно, работу А можно выразить произведением силы Р на путь S, т. е.

A = PS кГ*м. (25)

Работа, совершенная в единицу времени, называется мощностью и выражается формулой

N = A/t = (PS)/t = (pv)/60 [кГм/сек],(26)

где Р — сила, кГ;

v — скорость, м/мин.

Единицей измерения мощности является ватт (вт). Для выражения мощности в киловаттах применяют формулу N =A/(60*102) квт.

Часть мощности N _эф двигателя станка затрачивается на полезную работу, другая часть N_тр — на преодоление сил трения. Общая затрачиваемая мощность N=N_эф + N_тр.

Полезная работа является частью затраченной работы, а отношение полезной работы к затраченной называется коэффициентом полезного действия (к. п. д.) станка и обозначается буквойη(эта): η = (N_эф / N)* 100%. (27)

Чем меньше трение, тем большая часть мощности будет использована на полезную работу и, следовательно, выше к. п. д. станка.

Коэффициенты полезного действия работы некоторых систем и устройств составляют: ременной передачи с плоскими ремнями и натяжным роликом — 0,98, цепной передачи при хорошей смазке— 0,97, подшипников скольжения одного вала — 0,98, подшипников качения одного вала —0,99, пары зубчатых колес при хорошей смазке —0,99—0,993, червячной пары в зависимости от скорости вращения и смазки — от 0,3 до 0,97.

Механическая энергия.

Механическая энергия

Механическое состояние тела (системы тел) определяется его положением относительно других тел (координатами) и его скоростью.

Если изменяется хотя бы одна из этих величин, то говорят об изменении механического состояния тела.

Состояние данной системы тел обязательно изменяется, если внешние силы совершают отличную от нуля работу.

Количественно механическое состояние системы и его изменение характеризуется механической энергией W.

Механическая энергия — это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу. Изменение механической энергии ΔW равно работе приложенных к системе внешних сил:

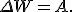
Значение энергии системы в данном состоянии не зависит от пути перехода ее в это состояние.

Закон сохранения энергии.

Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.

В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.

Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первого начала термодинамики, а в электродинамике — теорема Пойнтинга.

С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Билет №10

1. Механические колебания – это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве.   Различают периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени. Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него. В физике рассматривают и другие колебания – процессы, обладающие той или иной степенью повторяемости во времени, например, электромагнитные колебания. 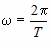Колебания можно классифицировать по условиям возникновения свободные, вынужденные, автоколебания и по характеру изменения во времени кинематических характеристик (пилообразные, гармонические, затухающие) 2. Колебательное движение это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени. Учение о колебательном движении в физике выделяют особо. Это обусловлено общностью закономерностей колебательного движения различной природы и методов его исследования. Механические, акустические, электромагнитные колебания и волны рассматриваются с единой точки зрения. Колебательное движение свойственно всем явлениям природы. Внутри любого живого организма непрерывно происходят ритмично повторяющиеся процессы, например биение сердца.

3. Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равени не зависит^[1] от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

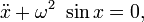
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 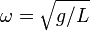где L ― длина подвеса, g ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид: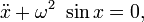

Билет№11

1. Колебательные движения, или просто колебания, широко распространены в природе. Заставить предмет колебаться, т. е. совершать повторяющиеся движения, очень просто.

Механические колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.

Повторяются движения поршней в двигателе автомобиля, поплавка на волне, ветки дерева на ветру, нашего сердца. Все это различные примеры колебаний.

Свободные колебания. Группу тел, движение которых мы изучаем, называют в механике системой тел или просто системой. Напомним, что силы, действующие между толами системы, называют внутренними. Внешними си-чами называют силы, действующие на тела системы со стороны тел, не входящих в нее.

Самым простым видом колебаний являются свободные колебания. Свободными колебаниями называются колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия и предоставлена затем самой себе.

Колебания груза, прикрепленного к пружине, или груза, подвешенного на нити, — это примеры свободных колебаний. После выведения системы из положения равновесия создаются условия, при которых груз колеблется без воздействия внешних сил.Однако с течением времени колебания затухают, так как на тела системы всегда действуют силы сопротивления. Под действием внутренних сил и сил сопротивления система совершает затухающие колебания.

Вынужденные колебания. Для того чтобы колебания не затухали, на тела системы должна действовать периодически изменяющаяся сила. Постоянная сила не может поддерживать колебания, так как под действием этой силы может измениться только положение равновесия, относительно которого происходят колебания.

Вынужденными колебаниями называются колебания тел под действием внешних периодически изменяющихся сил.

Колебания бывают свободными, затухающими и вынужденными. Наибольшее значение имеют вынужденные колебания. Ф.упр. ф.т

2. Уравнение гармонических колебаний можно записать в виде:
x = A*sin(wt + f₀), где

x - смещение точки от положения равновесия,
A - амплитуда колебаний,
(wt+f₀) - фаза колебаний,
f₀ - начальная фаза,
w - частота,
t - время.

гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.

3.Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
Для пределения условий возникновения режима резонанса в электрической цепи нужно:
· найти ее комплексное сопротивление или проводимость;
· выделить мнимую часть и приравнять нулю.
Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.
Уравнение Im[Z]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.
В электрических цепях резонанс может рассматриваться в задачах:
· анализа этого явления при вариации параметров цепи;
· синтеза цепи с заданными резонансными параметрами.
Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.

Билет№12

1. Скорость распространения волн:

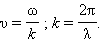Скорость распространения поперечных волн в струне:

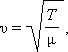T – натяжение; μ – погонная масса.

Скорость распространения продольных волн в упругом стержне

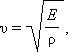E – модуль Юнга; ρ –плотность.

Скорость распространения продольных волн в безграничных средах:

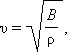B – модуль все стороннего сжатия; ρ – плотность.

Скорость звука в газе:

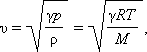T – абсолютная температура; R- универсальная газовая постоянная; M – молярная масса; γ = 1,4 (для двухатомных газов)

Частота звуковых биений:

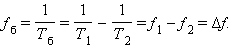Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.

Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.

Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.

Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

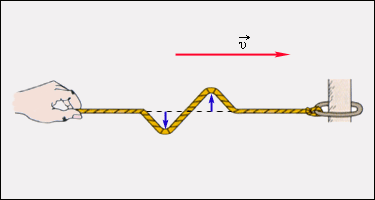Рисунок 2.6.1. Распространение поперечного волнового импульса по натянутому резиновому жгуту

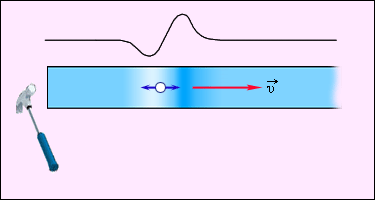Рисунок 2.6.2. Распространение продольного волнового импульса по упругому стержню