Расчет термодинамических констант равновесия

Термодинамическая константа равновесия может быть выражена как через активности веществ, участвующих в реакции, K_a, так и через фугитивности K_f:

,

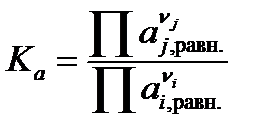
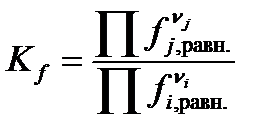Термодинамические константы равновесия являются безразмерными величинами.

Константа равновесия 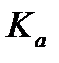может быть рассчитана по частному уравнению изотермы химической реакции:

,

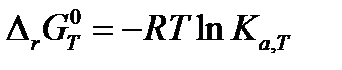(1.36)

если известно значение изменения стандартной энергии Гиббса при данной температуре. Тогда термодинамическая константа равновесия 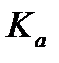рассчитывается как экспонента:

,

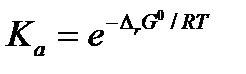Термодинамическая константа равновесия зависит от природы реагирующих веществ и температуры, но не зависит от давления, поскольку изменение стандартной энергии Гиббса не зависит от давления по определению.

Величина константы равновесия может принимать значения от нуля до бесконечности: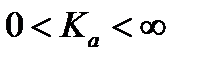

Пример: Рассчитаем термодинамическую константу равновесия реакции синтеза метанола при температурах 298 и 1000 К и давлении 101,325 кПа.

Решение:Рассчитаем изменение стандартной энергии Гиббса при температуре 298К, используя рассчитанные в предыдущих примерах значения 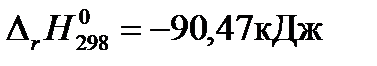и :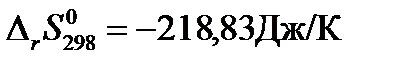

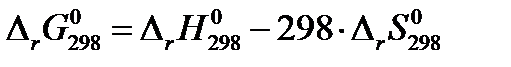= – 90,47∙10³ – 298∙( – 218,83) = – 25258,66 Дж

По частному уравнению изотермы химической реакции

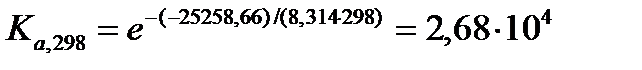
Для расчета константы равновесия при 1000 К воспользуемся рассчитанным в предыдущем примере значением стандартной энергии Гиббса при температуре 1000 К для реакции синтеза метанола .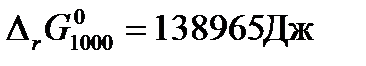

По частному уравнению изотермы химической реакции

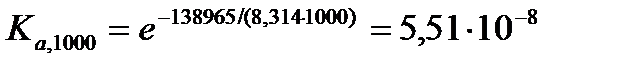
Если химическая реакция протекает при давлениях меньше ≤ 50 атм, то константа равновесия, выраженная через приведенные давления 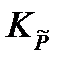, равна термодинамической константе равновесия K_aи является безразмерной величиной.

Практические константы равновесия

Химическое равновесие могут характеризовать практические константы равновесия. Практические константы равновесия могут быть рассчитаны, если при равновесии определить количества или концентрации веществ, участвующих в реакции тем или иным методом химического или физико-химического анализа. Они могут быть выражены

– через числа молей веществ n_i,j в равновесии:

;

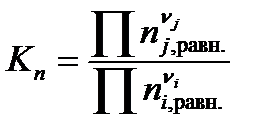(1.37)

– через молярные концентрации веществ с_i,j в равновесии:

;

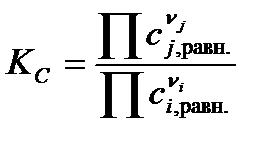(1.38)

– через мольные доли веществ x_i,j в равновесии:

;

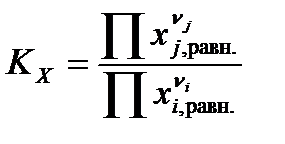(1.39)

– через парциальные давления веществ p_i,j в равновесии:

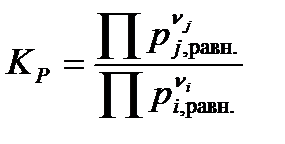(1.40)

Практические константы равновесия являются размерными величинами.

Удобно использовать и безразмерные константы равновесия, например, константу, выраженную через приведенные давления :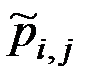

,

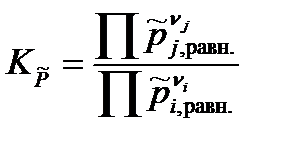(1.41)

где 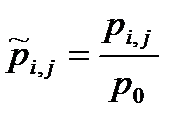, а p₀ – стандартное давление.

Между практическими константами равновесия существует определенная математическая связь. Например, легко показать, что константа 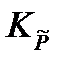связана с практической константой равновесия, выраженной через моли K_n,следующим соотношением

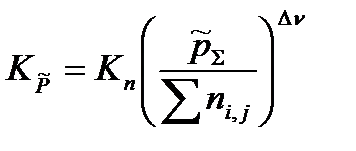(1.42)