Зависимость теплового эффекта реакции от температуры. Уравнение Кирхгоффа.

Теплоемкость – это количество теплоты необходимое для нагревания одного моль вещества на 1 градус.

Сv = (∂H/dT)v изохорн

Cp = (∂H/dT)p Уравнения Кирхгоффа частное производное теплового эффекта

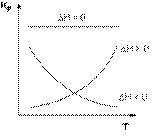
Cp – Сv = R если ΔCp>0 то с увеличением Т тепловой эффект р-ии возрастает.

(∂H/dT)p >0

Если ΔCp = 0 (∂H/dT)p = 0

Если ΔCp < 0 (∂H/dT)p < 0

Процессы обратимые и необратимые в термодинамическом смысле. Максимальная и минимальная полезная работа процесса.

Первый закон термодинамики не устанавливает направления тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми.

Обратимыми процессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.

Максимальная полезная внешняя работа A'max представляет собой работу, которую производит система над внешним теплоизолированным от системы объектом работы в обратимом процессе 1-2 работу, которую должен затратить внешний источник работы, чтобы вернуть систему из состояния 2 в исходное состояние 1 в тех же самых условиях, т.е. работу обратного обратимого процесса 2 - 1 называют минимальной работой; при этом A'max = - A'min

В самом общем случае состоит из двух частей: работы, связанной с изменением объёма, и работы , не связанной с изменением объёма.

Второе начало термодинамики и его математическое выражение. Энтропия – функция состояния системы. Изменение энтропии в изолированных системах.

Второе начало термодинамики устанавливает критерии самопроизвольного процесса его направление предел протекания, и количество работы которое при этом получено.

«Тепло не может самопроизвольно переходить от более холодного к более тёплому телу» (Р. Клаузиус).

«Невозможно построить "вечный двигатель второго рода", то есть периодически работающую машину, которая производила бы только подъём груза за счёт охлаждения теплового резервуара» (В. Оствальд).

[S] = [Дж/моль*к]

Эти формулировки тавтологично и строго утверждают, что энтропия есть функция состояния системы. dS=δQ/T Энтропия это функция состояния системы, бесконечно малое количество теплоты к термодинамической температуре.

Изолированные (замкнутые) системы не обмениваются веществом и энергией с окружающим пространством. В таких системах изменение энтропии ΔS = 0 (для обратимых процессов) и ΔS >0 (для необратимых). Все реальные процессы необратимые и поэтому энтропия в изолированной системе для самопроизвольных процессов может только возрастать, что указывает на однонаправленность всех процессов в природе. Этот вывод получил название закона возрастания энтропии.

Расчет изменения энтропии в изометрических процессах и при изменении температуры

Энтропия это экстенсивная величина. Т.е если разбивать процесс на стадии то энтропия будет равна сумме энтропий на каждой стадии.

-5…100°C

1) нагрев кристаллов воды -5-0°C

ΔS1 = n * Cp * ln T2/T1

T2 = -5+273

T1= 0+273

2)Фазовый переход (плавление льда)

ΔS2 = ΔHф.п / Т (273К)

3)Нагрев жидкой воды

0…100°C

ΔS3 = n * Cp * ln T2/T1

T2 = 373

T1= 273

4) Изменение агрегатного состояния

ΔS4 = ΔHф.п / Т

ΔS = ΔS1+ ΔS2+ ΔS3+ ΔS4

Статистический характер второго начала термодинамики. Вероятность состояния системы и изменение вероятности состояния при самопроизвольных процессах. Энтропия и ее связь с вероятностью состояния системы. Формула Больцмана.

Статистический характер энтропии описан Больцманом . Для изолированных систем.

S = K * lnω

где k = 1.38 10-23 Дж/К - постоянная Больцмана (k = R / NA), ω - так называемая термодинамическая вероятность, т.е. число микросостояний, которые соответствуют данному макросостоянию системы Формулу называют формулой Больцмана.

Статистический характер заключается в том что ур-е применимо только к макросистемам (большое число обьектов) от менее вероятного к более вероятному стремится система.

Термодинамические потенциалы. Энергия Гельмгольца (изохорно-изотермический потенциал) и ее связь с максимальной работой процесса. Стандартная энергия Гиббса и энергия Гельмгольца в самопроизвольных процессах. Критерии термодинамического равновесия.

Энергия Гиббса (изобарно-изотермический потенциал)

Энергия Гельм-Гольца (изохорно-изотермический потенциал)

В закрытых и открытых системах истинным критерием направленности является энергия Гиббса -G, и энергия Гельм-гольца – F. Исходя из 1 начала термодинамики δQ=dU+δA', если в системы кроме работы расширения совершается еще и полезная работа, то δA=δÁ'+PdV – общая полезная работа расширения

δQ = TdS отсюда следует

TdS = dU+ δÁ' + PdV

- δÁ' = dU + PdV - TdS

- δÁ' = d(U + PV – TS)

- δÁ' = d (H - TS)

- δÁ' = AG

ΔG = -A'max

Max полезная работа совершается за счет убыли энергии Гиббса при постоянной температуре и давлении. Основное ур-е термодинамики ур-е Гиббса ΔG =ΔH – TΔS T=298° Если процесс самопроизвольный то ΔG<0 при таком значении говорят о том что процесс самопроизвольный, протекает в прямом направлении в стандартных условиях.

1) ΔН<0 ΔS>0 отсюда следует ΔG<0

2) Если ΔН<0 ΔS<0 отсюда следует ΔG<0, если |ΔH|>|TΔS| при низких температурах

3) ΔН>0 ΔS>0 отсюда следует ΔG<0, если |ΔH|<|TΔS| при высоких температурах

ΔF=U – TS

ΔF=ΔU° – TΔS°

ΔFv,t = -A'max

ΔFp,t = 0 ΔGp,t = 0 это состояние химического равновесия

ΔFp,t > 0 ΔGp,t >0 то процесс не самопроизвольный он не идет в прямом направлении при данных условиях.