Давление насыщенных паров. критические и приведенные параметры, фугитивность жидких углеводородов нефти и нефтепродуктов

1.4. Давление насыщенных паров. Под давление насыщенных паров понимают давление, развиваемое парами, находящимися над жидкостью в условиях равновесия между жидкостью и паром при определенной температуре. При проведении практических расчетов исходя из допущения, что при испарении узкой нефтяной фракции состав паровой и жидкой фаз существенно не меняется, т.е. давление насыщенных паров зависит только от температуры. На этом базируются различные формулы [1], из которых чаще других используется формула Ашворта

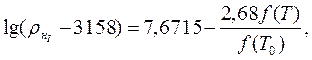(1.5)

где 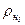- давление насыщенных паров при температуре Т, Па; Т₀ – средняя температура кипения фракции при атмосферном давлении, К.

Функция температур f(T) и f(T₀) выражается уравнением

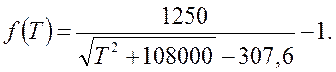
Значения функции при различных температурах даны в прил.4.

ПРИЛОЖЕНИЕ 4. Значение температурной функции f(T) для расчета давления насыщенных паров по формуле (1.5)

Температура, °С	f(T)	Температура, °С	f(T)	Температура, °С	f(T)	Температура, °С	f(T)
-40	12,122		5,595		3,144		1,952
-30	11,363		5,343		3,031		1,891
-20	10,699		5,107		2,924		1,832
-10	10,031		4,885		2,821		1,776
	9,448		4,677		2,724		1,721
	8,914		4,480		2,630		1,668
	8,421		4,297		2,542		1,618
	7,967		4,124		2,456		1,569
	7,548		3,959		2,375		1,521
	7,160		3,804		2,297		1,476
	6,800		3,658		2,222		1,432
	6,660		3,519		2,150		1,339
	5,155		3,387		2,082		1,348
	5,866		3,263		2,005	-	-

Формула Ашворта дает достаточно хорошие результаты, однако применима только при атмосферном давлении.

Пример 1.7 Определить давление насыщенных паров узкой бензиновой фракции при 150°С, если средняя температура кипения этой фракции составляет 95°С.

Решение. Для подсчета давления насыщенных паров воспользуемся формулой Ашворта (1.5).

Определим вначале по прил.4 значение функции f(T) и f(T₀) для температур 150°С и 95°С, причем для температуры 95°С с помощью интерполяции: f(T)=4,48 и f(T₀)=5,73.

Найденные значения подставляем в формулу (1.5):

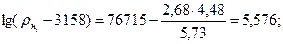
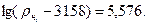
По таблицам антилогарифмов или с помощью микрокалькулятора определяем:

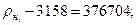
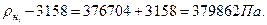
При необходимости пересчета давления насыщенных паров с одной температуры на другую или средней температуры кипения нефтепродукта при изменении давления используют номограммы (прил.5, 6). Номограмма прил.5 известна также как график Кокса, применимый для узких нефтяных фракций.

ЛИТЕРАТУРА

1. Расчёты основных процессов и аппаратов нефтепереработки : Справочник/ Под ред. Е.Н.Судакова.-М.:Химия, 1979.-568с.

2. Сарданашвили А.Г., Львова А.И. Примеры и задачи по технологии переработки нефти и газа.-М.:Химия, 1980.-256с.

3. Эрих В.Н., Расина М.Г., Рудин М.Г. Химия и технология нефти и газа-Л..-Химия, 1985.-424с.

4. Кузнецов А.А., Судаков Е.Н.Расчёты основных процессов и аппаратов переработки углеводородных газов: Справ, пособие.-М.:Химия, 1983-.224с.

5. Варгафтик Н.Б.Справочник по теплофизическим свойствам газов и жидкостей.-М.: Наука, 1972.-720с.

6. Технологические расчёты установок переработки нефти:Учеб. пособие для вузов/ Танатаров М.А., Ахметшина М.Н., Фасхутдинов Р.А. и др.-М.:Химия, 1987.-352с.

7. Рудин М.Г., Смирнов Г.Ф. Проектирование нефтеперерабатывающих и нефтехимических заводов .-Л.: Химия, 1984.-256с.

8. Рудин М.Г., Драбкин А.Е. Краткий справочник нефтепереработчика.-Л. Химия, 198О.-328с.

9. Справочник нефтепереработчика: Справочник/ Под ред. Г.А.Ластовкина, Е.Д.Радченко и М.Г. Рудина.-Л.: Химия, 198б.-648с

10. Хорошко С.И., Хорошко А.Н. Сборник задач по химии и технологии нефти и газа : Учеб. пособие для сред. спец. учеб. заведений.-Минск :Высш.шк., 1989.-122с.

11. Рябцев Н.И. Природные и искусственные газы.-М.:Стройиздат, 1978.-325с.

ПРИЛОЖЕНИЕ 5. График Кокса

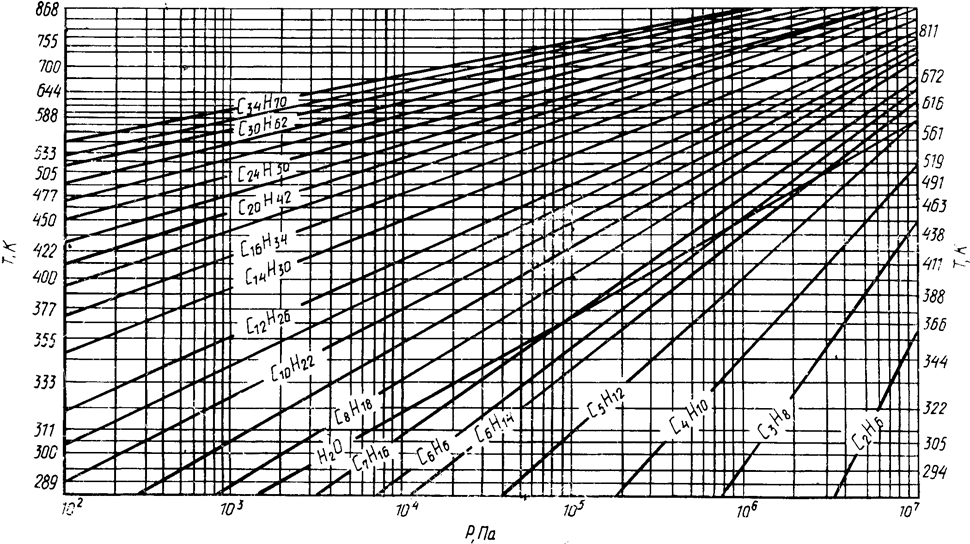
Пользование номограммой. На графике находим точку с координатами заданным давлением или температурой. Из найденной точки проводим равноудаленную от двух соседних лучей прямую до пересечения с вертикалью или горизонталью заданного углеводорода, соответствующей давлению этому давлению или температуре. Из полученной точки проводим горизонталь или вертикаль, параллельную оси абсцисс или ординат, до пересечения с осью на которой получим точку, соответствующую температуре или давлению.

ПРИЛОЖЕНИЕ 6. Номограмма для определения температуры кипения нефтепродуктов в зависимости от давления

Пользование номограммой. Через точку соответствующую заданному значению давления (правая шкала), провести прямую до пересечения с кривой (средняя шкала) температуры кипения заданного соединения при атмосферном давлении. Продолжение прямой укажет на температуру кипения соединения при заданном давлении (левая шкала)

Критические и приведенные параметры. При определенных значениях температуры и давления двухфазная система (жидкость – пар) может переходить в однофазную (пар), которая характеризует критическое состояние вещества. Температуру и давление, соответствующие этому состоянию, называют критическими. Для многих индивидуальных углеводородов они известны и приведены в различных литературных источниках [4, 5].

Приближенно критические параметры нефтяных фракций определяют с помощью графика (рис.1.2) по известным молярным массам, средним температурам кипения и относительной плотности.

Пример 1.8 Средняя температура кипения узкой бензиновой фракции при атмосферном давлении (»1×10⁵ Па) составляет 127°С. Найти ее температуру кипения при давлении 2×10⁵ Па.

Решение. На графике Кокса (прил. 5) находим точку с координатами 10⁵ Па и 127°С (400 К). Из найденной точки проводим равноудаленную от двух соседних лучей прямую до пересечения с вертикалью, соответствующей давлению 2×10⁵ Па. Из полученной точки проводим горизонталь, параллельную оси абсцисс, до пересечения с осью ординат, на которой получим точку, соответствующую температуре 151°С (424 К). Эта температура и является температурой кипения фракции при давлении 2×10⁵ Па.

Пример 1.9 При вакуумной разгонке нефтяного остатка в стандартном аппарате АРН-2 при давлении 133,3 Па была получена фракция 196-213°С. Каковы пределы выкипания этой фракции при атмосферном давлении?

Решение. Воспользуемся номограммой прил. 6. На правой шкале отметим остаточное давление 133,3 Па (1 мм рт.ст.), на левой – температуры начала и конца кипения фракции при данном давлении. Тогда на средней шкале получим точки, соответствующие температурам кипения при атмосферном давлении: 400°С и 420°С.

Таким образом, искомая фракция выкипает в пределах 400-420°С при атмосферном давлении.

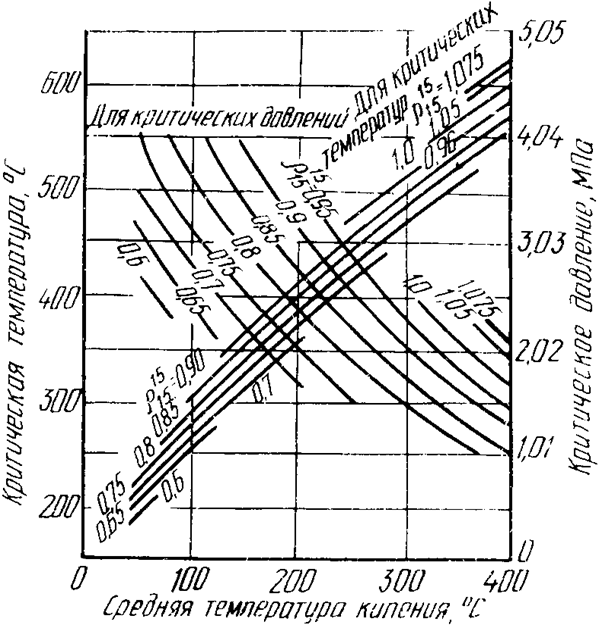
Рисунок 1.2 – График для определения критических температур и

давлений нефтепродуктов разной плотности

Более точно критическую температуру Т_кр (в кельвинах) и давление r_кр (в паскалях) можно найти по уравнениям:

Т_кр=355+0,97а+0,00049а²; (1.6)

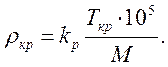(1.7)

Константы а и k_p, входящие в уравнения (1.6) и 1.7), рассчитываются по формулам:

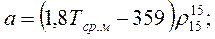
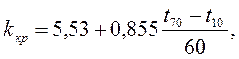
где t₁₀, t₇₀ – температуры отгона 10 и 70% нефтепродукта по ГОСТ 2177-82, °С.

Константа k_p имеет численные значения для парафиновых углеводородов 5,0-5,3; нафтеновых 6,0; ароматических 6,5-7,0; нефтепродуктов прямой перегонки 6,3-6,4 [2].

При определении константы а вместо средней молярной температуры кипения нефтяной фракции приближенно можно взять температуру ее 5-%-го отгона. Последняя также входит в упрощенную формулу подсчета критической температуры [1]:

Т_кр=1,05Т_ср+146.

При расчете тепловых и некоторых других свойств нефтепродуктов применяют так называемые приведенные температуру и давление.

Приведенная температура (Т_пр) представляет отношение температуры нефтепродукта (Т, К) в заданных условиях его критической температуре (Т_кр, К):

Т_пр=Т/Т_кр. (1.8)

Приведенное давление (r_пр) – это отношение давления в системе (r, Па), в которой находится нефтепродукт, к его критическому давлению (r_кр, Па):

r_пр=r/r_кр. (1.9)

Фугитивность. Нефтепродукты и их пары не всегда являются идеальными системами. При невысоких давлениях и повышенных температурах они подчиняются законам Рауля и Дальтона

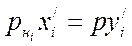или 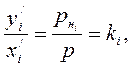(1.10)

где 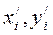– молярная доля i-го компонента в жидкой и паровой фазе; 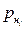– давление насыщенных паров i-го компонента, Па; р – общее давление в системе, Па; 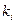– константа фазового равновесия.

Большие давления и низкие температуры вызывают более или менее значительное отклонение от идеального состояния, и в расчетные формулы необходимо вводить поправки. В этих случаях выражение для константы фазового равновесия (1.10) можно записать в виде

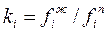или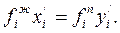

Здесь величины 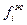и 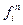представляют собой фугитивность жидкости и ее паров. Фугитивность измеряется в тех же единицах, что и давление, и заменяет его в уравнениях идеального состояния. Это позволяет использовать последние для реальных газов и жидкостей.

В общем случае фугитивность является функцией приведенных температуры и давления. Для практических целей фугитивность находят по графикам [1, 2, 6, 7], один из которых приведен на рис.1.3.

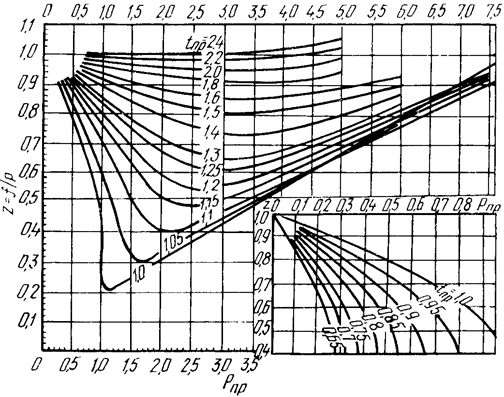
Рисунок 1.3 – График для определения коэффициента фугитивности

(сжимаемости) нефтепродуктов

Пользование номограммой. Через точку соответствующую заданному значению приведенного давления, провести прямую до пересечения с кривой заданного значения приведенной температуры. Из полученной точки пересечения провести горизонтальную прямую до шкалы коэффициентов сжимаемости. Точка пересечения дает искомое значение.

Ось ординат этого графика представляет собой отношение фугитивности к реальному давлению:

z=f/p. (1.11)

Безразмерная величина z носит название коэффициента фугитивности. Иногда его называют коэффициентом сжимаемости [7]. Хотя коэффициент сжимаемости имеет несколько иной физический смысл, при проведении приближенных расчетов можно допустить равенство названных коэффициентов.

Пример 1.12 Найти фугитивность фракции 62-85°С при 220°С и 2,5 МПа. Критические параметры t_кр=247°С и р_кр=3,56МПа.

Решение. Определим приведенные температуру и давление:

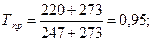
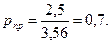
По графику (см. рис.1.3) находим коэффициент сжимаемости z=0,57. По формуле (1.11) фугитивность равна f=zp=1,43 МПа.

Пример 1.13 Определить константу фазового равновесия k для н-пентана при 115°С и 1,2 МПа. Его критические параметры: t_кр=0,57×2,5=3,34 МПа.

Решение. Найдем фугитивность для паровой фазы н-пентана. Приведенные параметры

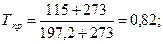
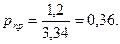
По графику (см. рис.1.3) определим z=0,76 и f^п=0,76×1,2=0,91 МПа.

Жидкая фаза находится при той же температуре, но под давлением собственных насыщенных паров р_н, которое определим по графику Кокса (прил.5): р_н=0,8 МПа. Приведенное давление в этом случае

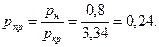
Коэффициент сжимаемости для жидкой фазы (см. рис.1.3) z=0,81, фугитивность жидкой фазы f^ж=0,81×0,8=0,65 МПа. Константа фазового равновесия определится как отношение фугитивностей

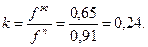
Кроме рассмотренного способа, константу фазового равновесия можно находить по номограммам (прил.7, 8).

ПРИЛОЖЕНИЕ 7. Таблица перевода значений кинематической вязкости (мм²/с) в условную (°ВУ)

мм2/с	°ВУ	мм2/с	°ВУ	мм2/с	°ВУ	мм2/с	°ВУ	мм2/с	°ВУ
	1,00		2,48		4,33		6,28		8,26
	1,10		2,60		4,46		6,42		8,40
	1,20		2,72		4,59		6,55		8,53
	1,29		2,83		4,72		6,68		8,66
	1,39		2,95		4,85		6,81		8,80
	1,48		3,07		4,98		6,94		8,93
	1,57		3,19		5,11		7,07		9,06
	1,67		3,31		5,24		7,20		9,20
	1,76		3,43		5,37		7,33		9,34
	1,86		3,56		5,50		7,47		9,48
	1,96		3,68		5,63		7,60		9,61
	2,05		3,81		5,76		7,73		9,75
	2,15		3,95		5,89		7,86		9,88
	2,26		4,07		6,02		8,00		10,01
	2,37		4,20		6,16		8,13		10,15

ПРИЛОЖЕНИЕ 8. Номограмма для определения константы фазового равновесия углеводородов при низких температурах

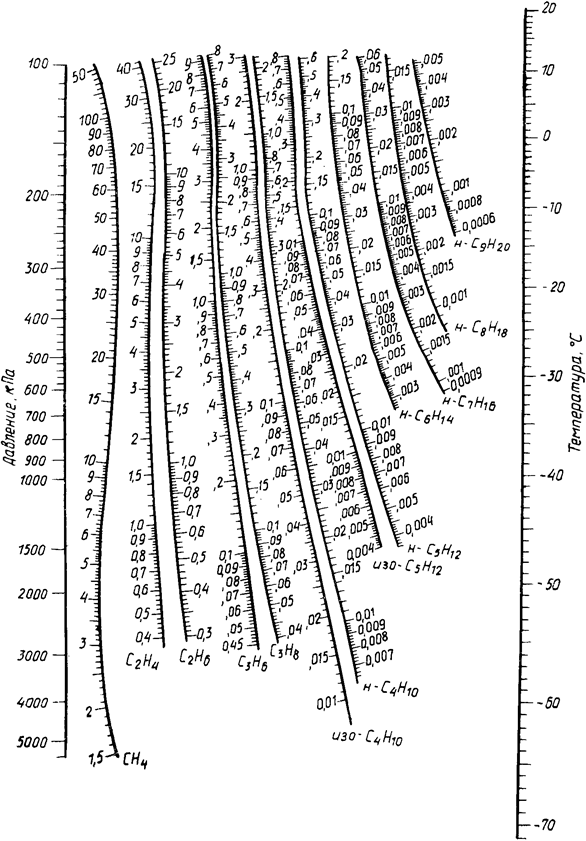
Пользование номограммой.Через точки, соответствующие заданным значениям давления и температуры провести прямую. Точка ее пересечения со шкалой констант фазового равновесия соответствующего углеводорода дает искомое значение.

ПРИЛОЖЕНИЕ 9. Номограмма для определения констант