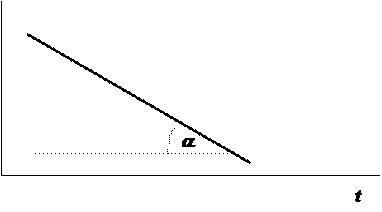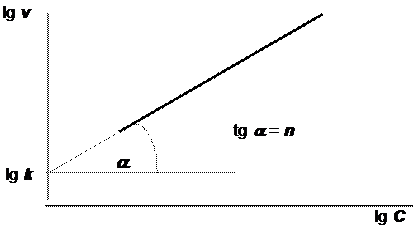Закон действующих масс. Константа скорости
В основе учения о химической кинетике лежит её основной постулат, который под названием “закон действующих масс”был открыт К.М.Гульдбергом и П.Вааге в 1864 - 67 г. г. (В некоторых учебниках можно встретить ошибочное выражение “закон действия масс”, которого следует избегать. К.М.Гульдберг и П.Вааге термином “действующая масса” обозначили то понятие, которое сейчас общепринято называют концентрацией. Термин “концентрация” был введён Я.Вант-Гоффом в 90-х годах XIX в.).
В современной формулировке закон читается так:
Скорость химической реакции в каждый момент времени пропорциональна произведению концентраций реагирующих веществ (имеющихся в данный момент времени), возведённых в некоторые степени.
Эти степени не всегда соответствуют стехиометрическим коэффициентам при формулах этих веществ в уравнении реакции, что было проиллюстрировано в п. 12.3.
Например, для произвольной реакции
aA + bB = dD + eE,
когда соотношение концентраций исходных веществ и продуктов близко к соотношению их стехиометрических коэффициентов, математическое выражение закона действующих масс будет выглядеть так:
v = k CaA CbB (12.3)
где CA и CB - концентрации исходных веществ А и В в данный момент времени; а и b - стехиометрические коэффициенты при формулах веществ А и В в уравнении реакции; k - коэффициент пропорциональности, называемый константой скорости данной реакции при данной температуре.
Уточнение о том, что показатели степени при концентрациях реагентов не обязательно совпадают со стехиометрическими коэффициентами, связано с упомянутым выше (п. 12.3) несовпадением порядка и молекулярности реакций. Оно становится понятным, если вспомнить, что показатель степени в уравнении (12.3) представляет собой порядок реакции, который может не соответствовать стехиометрии уравнения реакции и должен для каждого данного случая определяться экспериментально. Поэтому, если соотношения концентраций исходных веществ значительно отличаются от стехиометрии реакции, то степени при концентрациях в уравнении закона действующих масс должны быть соответствующим образом изменены.
Константа скоростиk численно равна скорости реакции в стандартном состоянии, то есть при концентрациях всех реагентов, равных 1 в выбранной системе единиц. Она количественно характеризует реакционную способность веществ в элементарной реакции при данной температуре в данной среде.
В случае сложных реакций, в особенности гетерогенных, константа в уравнении закона действующих масс называется коэффициентом скоростиили эффективной константой скоростии является эмпирической величиной, физический смысл которой определяется конкретным механизмом реакции.
Расчёт констант скорости для реакций различных порядков
Наибольшее практическое значение для фармации имеют реакции 1-го и 2-го порядков. Этим порядкам подчиняется подавляющее большинство реакций синтеза и разложения лекарственных веществ, а также реакций, используемых при различных методиках анализа.
Реакции первого порядка
Для произвольной реакции 1-го порядка вида
А ® продукты реакции
уравнение закона действующих масс выглядит так:
| dС v = - ¾¾ = kC , dt |
где С - концентрация вещества А. После разделения переменных
| dС k dt = - ¾¾ C |
это уравнение можно интегрировать в интервалах = 0 ¸ t, и С0 ¸ Сt:
| t Ct dС k ò dt = - ò ¾¾ , 0 C0 C |
получая при этом
k (t - t0) = - (ln Ct - ln C0)
или
k (t - t0) = ln C0 - ln Ct ,
откуда, принимая t0 = 0, получаем окончательное кинетическое уравнение для расчёта константы скорости реакции первого порядка:
| 1 С0 k = ¾ ln ¾¾ . (12.4) t Ct |
где С0 - начальная концентрация исходного вещества; Ct - концентрация, измеренная в момент времени t.
Из этого уравнения следует, что константу скорости реакции 1-го порядка можно определить графически, если построить график зависимости
ln С от времени. При этом тангенс угла наклона графика равен -k (рис. 12.2).
Строя график зависимости ln С от t для неизвестной реакции и получая при этом прямую линию, подобную изображённой на рис. 12.2, можно убедиться в том, что реакция имеет первый порядок.
Константа скорости может быть определена и без построения графика, а именно, как среднее арифметическое из величин, полученных при расчёте по уравнению (12.4) для нескольких текущих концентраций исходного вещества, экспериментально измеренных в различные моменты времени.
Так как в уравнение (12.4) входит отношение начальной и текущей концентраций, то в принципе оно может быть заменено отношением любых
Рис. 12.2. Зависимость ln С - t для реакции первого порядка |
других величин, пропорциональных концентрации (например, углов вращения плоскости поляризации реакционной смеси или её оптической плотности и т. п.), а сама концентрация может быть выражена любыми способами. Часто при вычислениях используют не концентрацию, а количество вещества в молях. Тогда расчётное уравнение для константы скорости будет выглядеть так:
| 1 а k = ¾ ln ¾¾¾ , (12.5) t а- х |
где а - начальное число молей исходного вещества, x - число молей его, прореагировавшее к моменту времени t.
С помощью уравнений (12.4) и (12.5) могут быть вычислены (если известна константа скорости) и другие важные кинетические характеристики, например, время полупревращения какой-либо реакции или, что представляет особый интерес для фармации, срок годности лекарственных препаратов.
Время полупревращения (t1/2) реакции удобно вычислять с помощью преобразованного уравнения (12.5):
| 1 а t = ¾ ln ¾¾¾ . k а - х |
Принимая х = а/2, получим:
| 1 а1 0,693 t1/2= ¾ ln ¾¾¾ = ¾ ln 2 = ¾¾¾, (12.6) k а - а/2 k k |
Это же выражение можно получить, используя уравнение (12.4) и принимая Ct = C0/2 .
Из уравнения (12.6) следует, что время полупревращения реакции первого порядкане зависит от начальной концентрации вещества. То есть для уменьшения концентрации, например, от 1 до 0,5 М потребуется ровно столько же времени, сколько для уменьшения концентрации от 0,001 до 0,0005 М. Из уравнения (12.6) следует также, что по экспериментально найденному значению t1/2 можно вычислить константу скорости реакции:
| 0,693 k = ¾¾¾ . t1/2 |
Реакции разложения многих лекарственных веществ, особенно реакции, идущие в растворах, являются реакциями первого или псевдопервого порядка, поэтому срок годностиих тоже может быть рассчитан по кинетическому уравнению (12.5). Согласно действующей нормативной документации лекарственный препарат считается годным к употреблению, если содержание лекарственного вещества в нём отвечает требованиям соответствующей фармакопейной статьи. Принимая, что в свежеприготовленном препарате количество наиболее быстро разлагающегося вещества а = 100%, а допустимый процент разложения лекарственного вещества равен х, можно, зная константу скорости разложения данного вещества при температуре его хранения, по уравнению
| 1100 t = ¾ ln ¾¾¾¾ . k 100 - х |
вычислить ориентировочный срок его годности.
Реакции второго порядка
Это самый распространенный тип реакций, которые могут протекать по схемам
1) А + В ® продукты реакции
или 2) 2А ® продукты реакции
Скорость таких реакций может быть описана такими уравнениями закона действующих масс:
для 1-го типа -
| dС v = - ¾¾ = kCACB , dt |
а для 2-го -
| dС v = - ¾¾ = kC2 . dt |
Далее мы будем рассматривать, главным образом, реакции, относящиеся к 1-му типу, как наиболее часто встречающиеся. Хотя следует помнить о том, что и реакции 2-го типа довольно широко распространены. В частности, разложение некоторых лекарственных веществ может протекать именно по этому типу.
Время, за которое вступает во взаимодействие определённая доля начального количества веществ, в реакциях второго порядка зависит от соотношения начальных концентраций исходных веществ. Поэтому принято рассматривать два возможных случая: 1) C0 A = C0 B и 2) C0 A ¹ C0 B.
При равных начальных концентрациях исходных веществ можно принять, что C0 A = C0 B = C0. При этом в каждый момент времени будет соблюдаться равенство Ct A = Ct B = Ct . Кинетическое уравнение для данного случая выглядит так:
| dС v = - ¾¾ = kC2. dt |
Разделяя переменные
| dС - ¾¾ = k dt C2 |
и интегрируя в интервалах = 0 ¸ t, и С0 ¸ Сt:
| t Ct dС k ò dt = - ò ¾¾ , 0 C0 C2 |
получаем
| 1 1 Ct - C0 kt = ¾ - ¾ = ¾¾¾¾ C0 Ct C0 Ct |
и окончательно
| 1 Ct - C0 k = ¾ · ¾¾¾¾ (12.7) t C0 Ct |
Заменяя концентрации на соответствующие количества вещества в моль
(C0 = а, Ct = а- х, и Ct - C0 = х), получим
| 1 х k = ¾ · ¾¾¾¾ . (12.8) t а(а- х) |
При различных начальных концентрациях исходных веществ, когда C0 A ¹ C0 B и Ct A ¹ Ct B, интегрирование кинетического уравнения
| dС v = - ¾¾ = k CA CВ dt |
или
| dС k dt = - ¾¾¾ CA CÂ |
даёт выражение
| 1 C0 B Ct A k = ¾¾¾¾¾¾¾ ln ¾¾¾¾ . (12.9) t (C0 A- C0 B) C0 A Ct В |
Заменяя концентрации на количество вещества (моль), получим
| 1 b(a - x) k = ¾¾¾¾ ln ¾¾¾¾ . (12.10) t (а - b) a(b - x) |
где а и b - соответственно начальное число молей веществ А и В; x - количество вещества, прореагировавшее к моменту времени t.
График зависимости 1/С от t для реакций второго порядка представляет собой прямую, проходящую через начало координат, с тангенсом, равным k; это означает, что константа скорости реакции второго порядка тоже может быть определена графически (рис. 12.3):
Рис. 12.3. Зависимость 1/С - t для реакции второго порядка |
Время полупревращения для реакции второго порядкарассчитывается с помощью выведенных уравнений по известной константе скорости. Для случая одинаковых начальных концентраций исходных веществ
| 1 1 t1/2= ¾¾ или t1/2= ¾¾ , kC0 kа |
для случая различных начальных концентраций
| 1 1 t1/2= ¾¾¾¾¾¾ или t1/2= ¾¾¾¾ . kC0 А - C0 В k (а - b) |
То есть, в отличие от реакций первого порядка, в данном случае время полупревращения зависит от начальной концентрации исходных веществ.
Определение порядка реакции
В соответствии с вышеизложенным порядок простой необратимой реакции может быть определён такими способами:
1) Интегральные методы.
1.1) По константам скорости. Процедура состоит в измерении концентрации реагента (или реагентов) в различные моменты времени и в подстановке полученных данных в уравнения для расчёта константы скорости реакции первого и второго порядка, выведенные ранее (а при необходимости и в уравнение для третьего порядка). То уравнение, которое для различных интервалов времени даёт значения константы скорости, характеризующиеся наименьшим разбросом значений, следует считать наиболее правильно отражающим порядок реакции. Если вычисления ни по одному из этих уравнений не дают удовлетворительных результатов (значения константы скорости во всех случаях имеют значительный разброс), то считается, что реакция имеет дробный порядок. В том случае, когда концентрация исходных веществ линейно уменьшатся с течением времени, принимается, что реакция имеет нулевой порядок.
1.2) По времени полупревращения. Метод аналогичен предыдущему, с тем различием, что в этом случае рассчитываются не k, а величины t1/2.
1.3) Графический. По экспериментальным данным строятся графики зависимостей для первого порядка ln C - t (см. рис. 12.2), для второго порядка 1/C - t (см. рис. 12.3), при необходимости для нулевого порядка C - t и для третьего порядка 1/C2 - t. Тот график, на котором точки лучше всего укладываются на прямую линию, соответствует порядку реакции.
2) Дифференциальный метод (по Вант-Гоффу, 1884)
Уравнение закона действующих масс для исследуемой реакции можно приблизительно записать в виде
v = kCn,
где n - суммарный порядок реакции. Логарифмируя это выражение, получим уравнение прямой, не проходящей через начало координат:
lg v = lg k + nlg C.
Построив по экспериментальным данным график зависимости логарифма скорости исследуемой реакции от логарифма концентрации одного из исходных веществ (рис. 12.4), можно определить её порядок как тангенс угла наклона графика к оси абсцисс. При этом от оси ординат отсекается отрезок, равный логарифму константы скорости реакции.
Рис. 12.4. Определение порядка реакции методом Вант-Гоффа |