Неориентированный граф
Дан список ребер графа с пятью вершинами V:{1,2,3,4,5} и E:{{1,2},{2,4},{2,5},{3,4},{3,5}}. Найти диаграмму графа, матрицы смежности и инцидентности, список смежности и степени вершин.
Диаграмма графа.
Построим матрицу инцидентности: размерность этой матрицы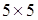 
, так как граф имеет пять вершин и пять ребер.
| е1 | е2 | е3 | е4 | е5 | |
Первое ребро е1 инцидентно двум вершинам 1 и 2, следовательно в первом столбце будут две единицы в первой и второй строке, а остальные элементы нули
| е1 | е2 | е3 | е4 | е5 | |
Второе ребро е2 инцидентно двум вершинам 2 и 4, следовательно во втором столбце будут две единицы во второй и четвертой строке, а остальные элементы нули.
| Е1 | е2 | е3 | е4 | е5 | |
Остальные столбцы заполняются аналогично.
| е1 | е2 | е3 | е4 | е5 | |
Построим матрицу инцидентности: размерность этой матрицы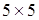 
, так как граф имеет пять.
Заполним главную диагональ матрицы, на ней ставится количество петель у каждой вершины, в нашем графе нет петель, поэтому в матрице на главной диагонали будет только 0.
Заполняем первую строку: вершина 1 соединена с вершиной 2 одним ребром, с 3 – 0 ребрами, с 4 – 0 ребрами, с 5 – 0 ребрами.
Заполняем вторую строку: вершина 2 соединена с вершиной 1 одним ребром, с 3 – 0 ребрами, с 4 – 1 ребром, с 5 – 1 ребром.
Остальные строки заполняются аналогично.
Матрица смежности вершин неориентированного графа симметрична относительно главной диагонали.
Список смежности.Вершина 1 соединена только с вершиной 2; вершина 2 – с 1, 4, 5; вершина 3 – с 4, 5; вершина 4 – с 2, 3; вершина 5 – с 2, 3. Составим список смежности:
{{2},{1,4,5},{4,5},{2,3},{2,3}}.
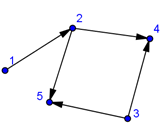Ориентированный граф.
Дан список ребер графа с пятью вершинами V:{1,2,3,4,5} и E:{(1,2),(2,4),(2,5),(3,4),(3,5)}. Найти диаграмму графа, матрицы смежности и инцидентности, список смежности и степени вершин.
Диаграмма графа.
Построим матрицу инцидентности: размерность этой матрицы 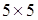, так как граф имеет пять вершин и пять ребер.
| е1 | е2 | е3 | е4 | е5 | |
Первое ребро е1 инцидентно двум вершинам 1 и 2, так как ребро ориентированно, то порядок вершин в записи ребра важен: 1 – начало ребра, 2 – конец ребра, поэтому в первом столбце и последней строке стоит -1, а в первом столбце и первой строке стоит 1, а остальные элементы нули.
| е1 | е2 | е3 | е4 | е5 | |
| -1 | |||||
Второе ребро е2 инцидентно двум вершинам 2 и 4: 2 – начало ребра, 4 – конец ребра, следовательно во втором столбце и второй строке стоит -1, а во втором столбце и четвертой строке стоит 1, а остальные элементы нули.
| Е1 | е2 | е3 | е4 | е5 | |
| -1 | |||||
Остальные столбцы заполняются аналогично.
| е1 | е2 | е3 | е4 | е5 | |
| -1 | |||||
| -1 | -1 | ||||
| -1 | -1 | ||||
Построим матрицу инцидентности: размерность этой матрицы 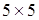, так как граф имеет пять.
Заполним главную диагональ матрицы, на ней ставится количество петель у каждой вершины, в нашем графе нет петель, поэтому в матрице на главной диагонали будет только 0.
Заполняем первую строку: вершина 1 соединена с вершиной 2 одним ребром, с 3 – 0 ребрами, с 4 – 0 ребрами, с 5 – 0 ребрами.
Заполняем вторую строку: вершина 2 соединена с вершиной 1 ни одним ребром, с 3 – 0 ребрами, с 4 – 1 ребром, с 5 – 1ребром.
Остальные строки заполняются аналогично.
Список смежности.Вершина 1 соединена только с вершиной 2; вершина 2 – с 4 и 5; вершина 3 – с 4, 5; вершина 4 – ни с одной; вершина 5 – ни с одной. Составим список смежности:
{{2},{4,5},{4,5},{},{}}.
Практическая работа.
Задание 1. 1. Для псевдографа с 7 вершинами и 13 ребрами построить диаграмму, матрицы смежности и инцидентности, списки ребер и смежности.
2. Для псевдоорграфа с 7 вершинами и 19 ребрами построить диаграмму, матрицы смежности и инцидентности, списки ребер и смежности.
3. Без помощи диаграммы по известной матрице инцидентности неориентированного псевдографа восстановить его список ребер и матрицу смежности.
а б в
| v1 | v2 | v3 | v4 | v5 | v1 | v2 | v3 | v4 | v5 | v6 | v1 | v2 | v3 | v4 | v5 | |||||
| е1 | е1 | е1 | ||||||||||||||||||
| е2 | е2 | е2 | ||||||||||||||||||
| е3 | е3 | е3 | ||||||||||||||||||
| е4 | е4 | е4 | ||||||||||||||||||
| е5 | е5 | е5 | ||||||||||||||||||
| е6 | е6 | е6 | ||||||||||||||||||
| е7 | е7 | е7 | ||||||||||||||||||
| е8 | е8 | е8 |
4. Без помощи диаграммы по известной матрице смежности неориентированного псевдографа восстановить его матрицу инцидентности и определить степени всех вершин.
а б в
5.Без помощи диаграммы по известной матрице инцидентности ориентированного псевдографа восстановить его список ребер и матрицу смежности.
а б в
| v1 | v2 | v3 | v4 | v5 | v1 | v2 | v3 | v4 | v5 | v6 | v1 | v2 | v3 | v4 | v5 | |||||
| е1 | -1 | е1 | -1 | е1 | -1 | |||||||||||||||
| е2 | е2 | -1 | е2 | -1 | ||||||||||||||||
| е3 | -1 | е3 | -1 | е3 | -1 | |||||||||||||||
| е4 | -1 | е4 | е4 | -1 | ||||||||||||||||
| е5 | -1 | е5 | -1 | е5 | -1 | |||||||||||||||
| е6 | -1 | е6 | -1 | е6 | -1 | |||||||||||||||
| е7 | -1 | е7 | -1 | е7 | -1 | |||||||||||||||
| е8 | -1 | е8 | -1 | е8 |
6. Без помощи диаграммы по известной матрице смежности ориентированного псевдографа восстановить его матрицу инцидентности и определить степени всех вершин.
а б в