Система М.О. з очікуванням
С.М.О. називається системою з очікуванням, якщо заявка, що застала всі канали зайнятими, стає в чергу і чекає, поки не звільниться який-небудь канал.
Якщо час очікування заявки в черзі нічим не обмежений, то система називається «чистою С.М.О. із очікуванням».
Якщо воно обмежено якимись умовами, то С.М.О. називається С.М.О. зміщеного типу. Це проміжний випадок між С.М.О. із відмовами і С.М.О. із очікуванням представляє найбільший інтерес для практики.
Обмеження, накладені на очікування:
1) за часом очікування заявки в черзі, рахується, що воно обмежене поверх Точ, випадковим або ні. Під часом очікування розуміється тільки строк у черзі, а почате обслуговування доводиться до кінця (клієнт у перукарні);
2) за часом перебування заявки в системі (повітряна ціль знаходиться в зоні стрільби обмежений час і залишає її незалежно від того, скінчився обстріл або ні).
3) за числом заявок у черзі (торгівля).
Розглянемо, як саму актуальну, третю задачу.
Нехай є, n-канальна С.М.О. Заявка стає в чергу, якщо усе n-каналів зайняті, і якщо в черзі менше m заявок. Якщо рівно m заявок у черзі, то остання заявка, що надійшла в чергу не стає і залишає систему.
Потоки заявок і обслуговування найпростіші з інтенсивністю l і m. У системи n+m+1 стан.
Sk - k каналів зайняті, черги немає, k = 0, ... , n
Sn+i - n каналів зайняті, i заявки знаходяться у черзі i = 1, ... , m
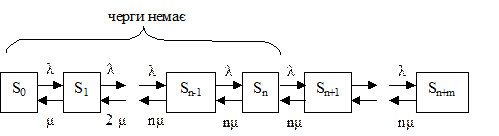 Мал. 11. Мал. 11. |
Граф станів такої С.М.О., мал.11. Складемо диф. рівняння для ймовірностей системи.
Очевидно, що перші n рівнянь для ймовірностей P0(t), P1(t), ..., Pn-1(t) будуть збігатися з рівняннями Ерланга, тому що граф станів від S0 до Sn-1 той же, що і в С.М.О. з відмовами. Виведемо інші рівняння, використовуючи правила для Н.М.Л.
P¢n = lPn-1(t) - (l+nm) Pn(t) + nmPn+1(t)
----------------------------------------------
P¢n+k = lPn+k-1(t) - (l+nm) Pn+k(t) + nmPn+k+1(t) (2.49)
----------------------------------------------
P¢n+m = lPn+m-1(t) - nmPn+m(t)
Додавши перші n диф. рівнянь одержимо систему диф. рівнянь для С.М.О. із чергою.
P¢0 = lP0(t) + mP1(t)
------------------------------------
P¢k-1 = lPn-2(t) - (l+(n-1)m) Pn-1(t) + nmPn(t) (2.50)
Тому що для Н.М.Л. у даному випадку виконується ерготична властивість, то розглянемо граничний випадок при
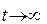
Тоді існує 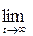 Pk(t) = Pk и все P¢k = 0
Pk(t) = Pk и все P¢k = 0
З (2.50) одержимо систему алгебраїчних рівнянь
- lP0 + mP1 = 0
---------------------------------
lPk-L -(l+Km)Pk + (K+1)mPk+1 = 0 2<k<n-1
--------------------------------- (2.51)
lPn+s-1 -(l+nm)Pn+s + nmPn+s+1 = 0 1<s<m-1
lPn+m-1 - nmPn+m = 0
і 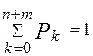 (2.52)
(2.52)
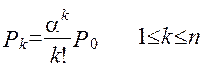 (2.53 )
(2.53 )
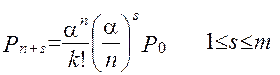 (2.54)
(2.54)
З (2.52) - (2.54) 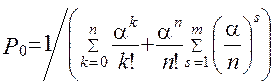 .
.
Якщо позначити 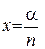 , то
, то 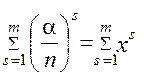 - геометрична прогресія з q = x; b1 = x
- геометрична прогресія з q = x; b1 = x
Тоді
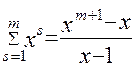 і
і 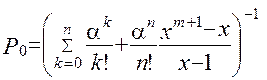 (2.55)
(2.55)
Ймовірність відмови
Рвідм. = Рn+m = xm 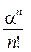 Р0 (2.56)
Р0 (2.56)
Відносна пропускна спроможність
q = 1 - Pвідм. = 1 - 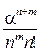 P0 (2.57)
P0 (2.57)
Абсолютна пропускна спроможність С.М.О.
А = lq = l(1 - 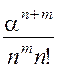 P0) (2.58)
P0) (2.58)
Знайдемо середнє число зайнятих каналів. Для С.М.О. із відмовами воно збігається із середнім числом заявок, що знаходяться в системі. Для С.М.О. із чергою середнє число зайнятих каналів не збігається із середнім числом заявок, що знаходяться в системі: остання величина відрізняється від першої на середнє число заявок, що знаходяться у черзі. Нехай k - середнє число зайнятих каналів, а z - середнє число заявок у системі. Кожний зайнятий канал обслуговує в середньому m заявок у од. часу, уся С.М.О. обслуговує в середньому А заявок у од. часу.
Тоді
q = 1 - Pвідм. = 1 - 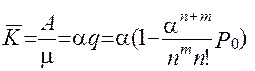 (2.59)
(2.59)
Середнє число заявок 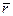 у черзі можна обчислити безпосередньо, як мат. сподівання числа заявок у черзі:
у черзі можна обчислити безпосередньо, як мат. сподівання числа заявок у черзі:
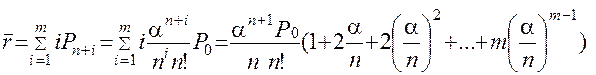 Якщо позначити x=α/n, то
Якщо позначити x=α/n, то
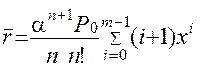 (2.60)
(2.60)
З огляду на, що
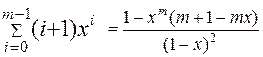 (2.61)
(2.61)
одержимо
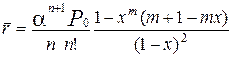 1 (2.62)
1 (2.62)
Складаючи 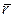 і
і 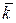 , одержимо середнє число заявок у системі:
, одержимо середнє число заявок у системі: 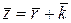 (2.63)
(2.63)
Знайдемо середній час очікування в черзі Точ.
Стани системи утворюють повну групу подій S0, S1,…,Sn+m. Для перших n подій S0, S1,…,Sn-1 черги немає. Тоді час очікування в цих випадках = 0. Якщо заявка надійде у момент, коли усі n каналів зайняті, а черги немає, тобто у випадку події Sn, їй доведеться очікувати в середньому 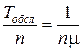 . У випадку події Sn+r, тобто r заявок у черзі
. У випадку події Sn+r, тобто r заявок у черзі 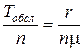 (r=1,. .,m-1).
(r=1,. .,m-1).
Тоді 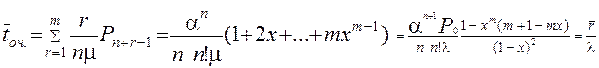 (2.64 )
(2.64 )
Середній час перебування заявки в системі Тсист
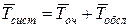 , де
, де 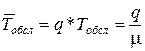 , Тобсл - обслуговування одним каналом першої заявки.
, Тобсл - обслуговування одним каналом першої заявки.
Тоді
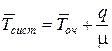 (2.65)
(2.65)
Приклад 8. На станцію поточного ремонту автомашин надходить найпростіший потік заявок із щільністю λ = 0,5 машин/год. Є одне приміщення для ремонту. В подвір'ї станції можуть знаходитися одночасно, очікуючи черги, не більш трьох машин. Середній час ремонту однієї машини mtоб=1/μ=2год. Визначити:
а) пропускну спроможність системи;
б) середній час простою станції;
в) визначити наскільки зміняться ці характеристики, якщо обладнати друге приміщення для ремонту.
Рішення. Маємо λ =0,5; μ =0,5; n=1; m=3; α =λ /μ=1.
a) По формулі (56) знаходимо Pвідм=P1+3=1/(1+1+3)=1/5=0,2. Тоді відносна пропускна спроможність системи q=1-Pвідм=0,8. Абсолютна пропускна спроможність А=λ´q=0,5´0,8=0,4 маш/год.
б) Вважаючи n=2 знайдемо за (2.56) Pвідм=P2+3=(1/16)/(1+1+1/2+1/4+1/8+1/16)=1/47=0,021. q=1-Pвідм=0,979, тобто задовольнятися будуть біля 98% заявок. Абсолютна пропускна спроможність А=λ´q=0,49 маш/год. Відносний час простою P0=16/47=0,34, тобто устаткування буде простоювати 34% усього часу.
Приклад 9. Автозаправочна станція (АЗС) з двома колонками (n=2), найпростіший потік машин інтенсивності λ=2 машин/год. Середній час обслуговування однієї машини tоб=2 хв. Площадка в АЗС може вмістити не більш m=3 машин. Машина, що прибула в момент, коли всі три місця на площадці зайняті, покидає АЗС. Знайти характеристики С.М.О.: можливість відмови; відносну та абсолютну пропускну спроможності;
1) середнє число зайнятих колонок;
2) середнє число машин у черзі;
3) середній час очікування і перебування машини на АЗС.
Перерахувати ці характеристики, якщо одна колонка вийде з ладу.
Рішення.
λ=2; μ =0,5; n=2; m=3; α =4; x=α /n=4/2=2
1) по формулах (2.56) та (2.57) Pвідм=P5=45/(232!)P0, P0=1/(1+4/2+42/2*(2-24)/(1-2))=0,008.
Pвідм=64×0,008=0,512
2) відносна пропускна спроможність q=1-Pвідм=0,488. Абсолютна пропускна спроможність А=λ*q=2*0,488=0,976 маш/хв.
3) середнє число зайнятих каналів (колонок)
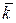 =А/μ =α×q=4×0,488=1,952, тобто обидві колонки майже весь час зайняті.
=А/μ =α×q=4×0,488=1,952, тобто обидві колонки майже весь час зайняті.
4) Середнє число машин у черзі знаходимо по (2.62)
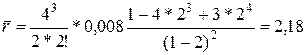 маш.
маш.
5) середній час очікування 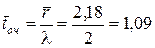 хв.
хв.
Середній час перебування машини на АЗС: 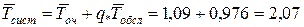 хв.
хв.
Для одноканальної С.М.О. λ = 2; μ = 0,5; n=1; m=3; α =4; x=α /n=4/1=4
Pвідм=P3+1=44(1-4)/(1-45)=3*256/1023=256/341=0,75.
q=1-0,75=0,25 А=λ*q=0,25*2=0,5 маш/год.
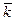 =А/μ =α*q=4*0,25=1, тобто колонка весь час зайнята
=А/μ =α*q=4*0,25=1, тобто колонка весь час зайнята
По формулі 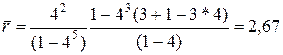 маш.
маш.
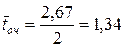 хв.
хв.
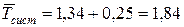 хв.
хв.
