Метод реинтеграции (метод нити Ариадны)

СОДЕРЖАНИЕ

1 Метод реинтеграции (метод нити Ариадны)……………………………3

Заключение……………………………………………………………… 10

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ…………………… 11

Метод реинтеграции (метод нити Ариадны)

Вспомним веселую историю, рассказанную английским писателем Джеромом К. Джеромом в книге “Трое в лодке”. Сколько людей смеялось над чудаком Гаррисом, попавшим в Хемптон-Кортский лабиринт!

— Мы только зайдем сюда, чтобы ты мог сказать, что побывал в лабиринте, но это совсем не сложно. Даже нелепо называть его лабиринтом. Мы походим здесь минут десять, а потом отправимся завтракать, — уговаривал Гаррис своего родственника.

Но увы! Он не только заблудился сам, но и запутал людей, которых взялся избавить от мучительного блуждания по лабиринту. За ним следовало по крайней мере человек двадцать и даже одна женщина с ребенком, безуспешно искавшая выход из лабиринта все утро.

Следуя своей тактике, Гаррис все время поворачивал направо. Ему казалось, что вот-вот он выберется из лабиринта. Но время шло, и вся компания во главе с Гаррисом вернулась к тому месту, где они уже были. Половинка булочки, брошенная ребенком и замеченная родственником Гарриса семь минут тому назад, с несомненностью указывала место их недавнего пребывания.

Тогда Гаррис предложил вернуться назад и начать все снова. Предложение начать снова особого энтузиазма не вызвало, но все согласились вернуться.

Процессия повернула обратно и потянулась за Гаррисом в противоположном направлении, но через десять минут вся компания снова очутилась в центре лабиринта. Такой же неудачей закончились и последующие попытки. В какую бы сторону они ни сворачивали, все пути приводили их в центр. Это стало повторяться с такой правильностью, что некоторые просто оставались на месте и ждали, пока остальные прогуляются и вернутся к ним.

Наконец отчаявшиеся любители лабиринта призвали на помощь сторожа, который и вывел их на “свободу”.

Бедному Гаррису не пришлось бы блуждать и мучить людей, если бы он знал алгоритм поиска путей в лабиринте. Таких алгоритмов существует несколько. Один из них связан с древнегреческим мифом о легендарном герое Тезее, который отважился проникнуть в лабиринт для того, чтобы разыскать в нем чудовищного Минотавра и убить его. Ему помогла выбраться из лабиринта Ариадна, давшая Тезею клубок ниток, один конец которых держала она сама. По мере углубления Тезея в лабиринт клубок разматывался; наматывая потом нитки, Тезей благополучно вернулся к выходу.

Представим себе лабиринт в виде конечной системы площадок, от которых расходятся коридоры, причем каждый коридор соединяет две площадки (такие площадки будем называть смежными), но не исключается существование таких площадок, из которых можно пройти только в один коридор (такие площадки будем называть тупиками). Геометрически лабиринт можно представить в виде системы точек А, В, С, … (изображающих площадки) и совокупности отрезков АВ, ВС, … (изображающих коридоры), соединяющих некоторые пары этих точек (рис. 1).

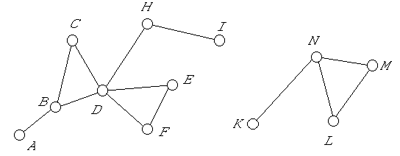
Рисунок 1

Будем говорить, что площадка Y достижима из площадки X, если существует путь, ведущий от X к Y через промежуточные коридоры и площадки. Точнее, это означает, что, либо X и Y — смежные площадки, либо существует последовательность площадок Х₁, Х₂, Х₃, ..., Х_n, таких, что пары площадок Х и Х₁, Х₁ и Х₂, Х₂ и Х₃, …, Х_n и Y смежны. Например, на приведенном рисунке площадка Н достижима из тупика А посредством пути АВ, ВС, СD, DЕ, ЕF, FD, DН, в то время как площадка K не достижима из А. Вместе с тем, если Y вообще достижима из X, то она достижима и посредством простого пути, т.е. такого пути, в котором каждая площадка (а тем более и каждый коридор) проходится лишь один раз. В предыдущем примере путь не был простым, но, срезав петлю DЕ, ЕF, FD, мы получаем простой путь АВ, ВС, СD, DН.

Предполагается, что Минотавр находится на одной из площадок лабиринта (обозначим ее М), а Тезей, отправляясь на его поиски с площадки А, на которой его ждет Ариадна, должен решить следующую задачу: требуется выяснить, достижима ли М из А или нет. Если достижима, то нужно добраться до нее по какому бы то ни было пути, но вернуться к Ариадне нужно уже по простому пути. Если же М недостижима, то вернуться к Ариадне.

Различных лабиринтов может быть бесчисленное множество, а взаимное расположение в данном лабиринте площадок А и М также можно варьировать. Поскольку Тезею заранее ничего не известно об устройстве данного лабиринта и о местонахождении в нем Минотавра, то решение поставленной задачи мыслится в виде общего метода поисков, пригодного при любом лабиринте и при любом расположении в нем площадок А и М. Иными словами, решение мыслится в виде алгоритма, решающего любую из задач данного типа (именно в этом, как известно, заключается такое свойство алгоритма, как массовость).

Алгоритм поиска. Для построения такого алгоритма мы рассмотрим один специальный метод поисков. На любой стадии процесса поиска в соответствии с этим методом приходится различать коридоры:

1) еще ни разу не пройденные Тезеем (условно — зеленые);

2) пройденные один раз (желтые);

3) пройденные дважды (красные).

Далее, находясь на какой-либо площадке, Тезей может попасть на одну из смежных площадок посредством одного из следующих двух ходов:

1. Разматывание нити. Прохождение от данной площадки по любому зеленому коридору до смежной площадки. При этом нить Ариадны разматывается вдоль этого коридора, который после прохождения уже считается желтым.

2. Наматывание нити. Возвращение от данной площадки по последнему пройденному желтому коридору до смежной площадки. При этом нить Ариадны, ранее размотанная вдоль этого коридора, наматывается обратно, а этот коридор уже объявляется красным.

Предполагается, что Тезей делает какие-то пометки, позволяющие ему впоследствии отличать зеленые коридоры от зеленых; желтые различимы тем, что по ним протянута нить Ариадны. Выбор того или иного хода зависит от обстановки, наблюдаемой Тезеем на той площадке, на которой он находится в данный момент; эту обстановку можно охарактеризовать одним или несколькими из следующих признаков:

1. Минотавр. На данной площадке обнаружен Минотавр.

2. Петля. Через данную площадку уже протянута нить Ариадны; иными словами, от площадки расходятся по крайней мере два желтых коридора.

3. Зеленая улица. На данной площадке есть выход по крайней мере в один зеленый коридор.

4. Ариадна. На данной площадке находится Ариадна.

5. Пятый случай. Отсутствие всех предыдущих признаков.

Наш метод поиска может быть теперь задан следующей схемой (см. табл. 1):

Находясь на какой-нибудь площадке, Тезей делает очередной ход так: он проверяет по порядку номеров в левом столбце схемы, какой из перечисленных признаков имеет место; обнаружив первый такой признак, он (уже не проверяя остальные признаки) делает соответствующий ход (или остановку) из правого столбца. Такие ходы делаются до тех пор, пока не наступит остановка.

Таблица 1

Пригодность предложенного метода непосредственно вытекает из следующих трех утверждений:

1. При любом взаимном расположении А и М в лабиринте после конечного числа ходов обязательно наступит остановка либо на площадке Минотавра, либо на площадке Ариадны.

2. Если остановка наступила на площадке Минотавра, то Минотавр достижим. Более того, в этом случае нить Ариадны оказывается протянутой по простому пути, ведущему от А до М; наматывая нить, Тезей может теперь вернуться по этому пути к Ариадне.

3. Если остановка наступила на площадке Ариадны, то Минотавр недостижим.

С доказательством этих утверждений можно познакомиться, например, в [1].

Посмотрим на двух примерах, как работает предложенный метод.

Пример 1. Пусть с площадки А лабиринта (см. рис. 1) начинается поиск Минотавра, который находится в F. Процесс поиска в соответствии с нашим методом удобно изобразить посредством схемы, представленной в табл. 2 (из-за свободы в выборе зеленого коридора — это лишь одна из возможных схем).

Мы видим, что в данном случае Минотавр достижим. Выделив в предпоследнем столбце те из коридоров, которые остались желтыми (в соответствии с показаниями последнего столбца), получим следующий простой путь, ведущий от А к F: АВСDF.

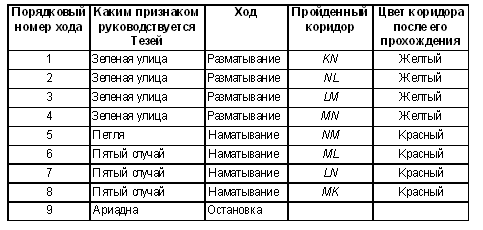
Пример 2. Если же поиск начинается с площадки К, то процесс поиска можно отразить в схеме, представленной в табл. 3.

Мы видим, что в этом случае Минотавр недостижим.

Заметим, что описанный алгоритм не обладает свойством определенности — с какой-то площадки могут оказаться выходы в несколько зеленых коридоров, а наше предписание не указывает, какой из них выбрать, точнее — оно допускает произвольный выбор одного из них. Чтобы это свойство соблюдалось, необходимо регламентировать, как должен проводиться выбор очередного проверяемого коридора в таких ситуациях.

Таблица 2

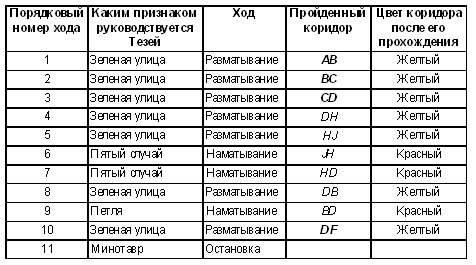
Таблица 3

Заключение

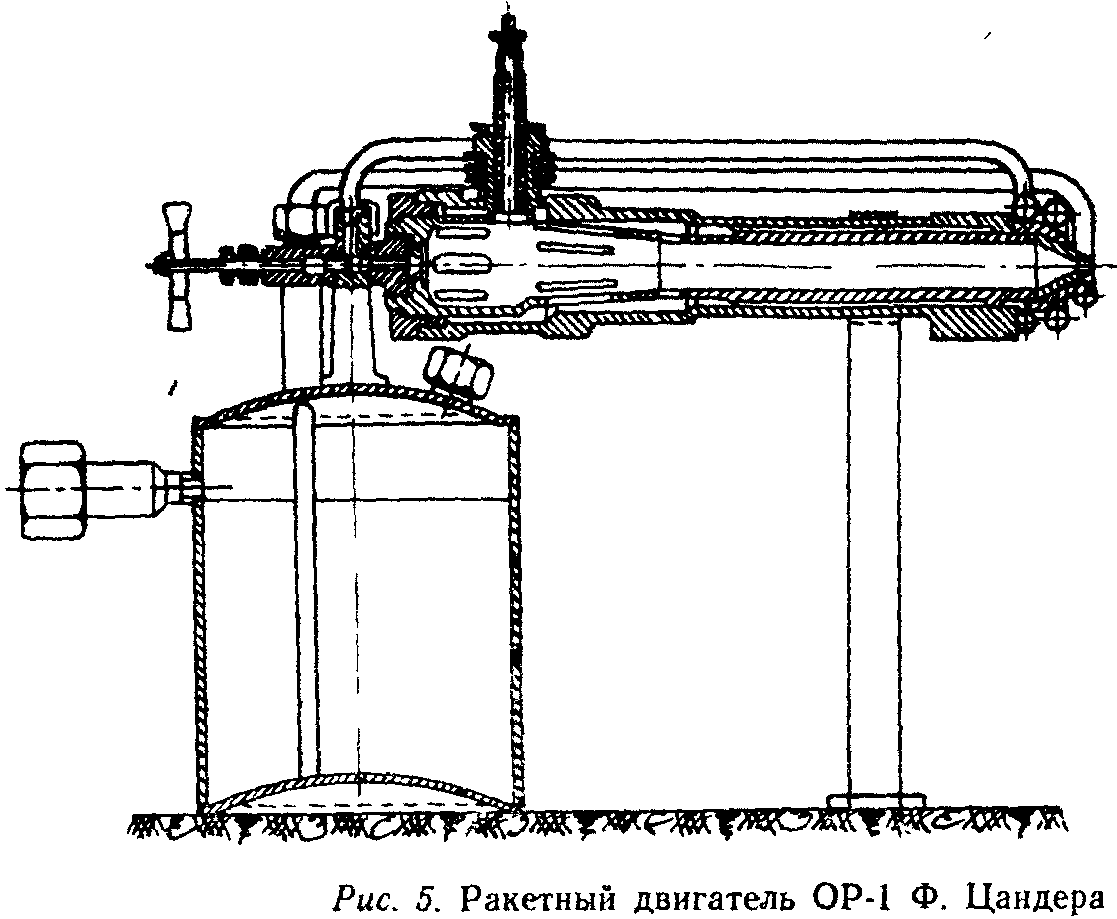
Метод реинтеграции (метод нити Ариадны) заключается в создании нового сложного технического объекта или процесса по аналогии с одной особо значащей деталью, операцией или простым техническим объектом. Известный изобретатель Ф. Цандер в 1930 г. создал свой ракетный двигатель ОР-1 по аналогии с паяльной лампой.

Он имел камеру сгорания с соплом, которое охлаждалось топливной смесью, подачу горючего и окислителя под давлением, электрическое зажигание и развивал тягу в 5 килограммов. Цандер измерил тягу с помощью рычажных весов.