Короткі теоретичні відомості. Аналоговими називають сигнали, що представляють собою безупинні функції часу.

Аналоговими називають сигнали, що представляють собою безупинні функції часу.

Відповідно, коло з RLC- елементів, керованих джерел струму і напруги (роль яких наприклад, можуть грати діоди, транзистори, операційні підсилювачі) будемо називати аналоговими.

Математичними моделями аналогових кiл є - диф. рівняння, КЧХ, передатні функції.

З метою підвищення якості обробки сигналів і використання для цих цілей спеціалізованих чи мікропроцесорів просто програми універсальних ЕОМ аналогові сигнали заміняються їхніми дискретними уявленнями- числовими послідовностями. Для повного відновлення сигналу його необхідно дискретизовать за часом з інтервалом Δt<=π/ω_max , де ω_max – максимальна частота в спектрі безупинного сигналу.

Позначимо дискретні отсчёты безупинного сигналу x(nΔt)=x(n).

Дискретним колом назвемо коло, що перетворить послідовність вхідних сигналів x(n) у послідовність y(n).

Аргумент n при цьому називається дискретним часом.

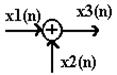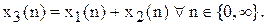Суматором послідовностей назвемо коло, що виконує математичну операцію підсумовування:

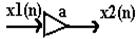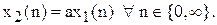Перемножником на постійний коефіцієнт будемо називати коло, яке реалізуе функцію:

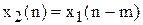Елементом затримки на число інтервалів часу m будемо називати коло із властивостями:

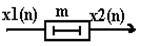Лінійними цифровими фільтрами (ЛЦФ) будемо називати кола, що складаються із сумматорів, перемножників, елементів затримки (елементів, що здійснюють лінійні операції над вхідними сигналами дискретного типу).

Приклад ЛЦФ та алгоритм його роботи.

Подамо сигнал x(n) на вхід ЛЦФ зі схемою:

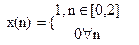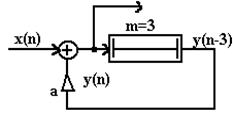Виразимо математично вихідний сигнал y(n): y(n)=x(n)+ay(n-3) (3.1)

Рівняння (3.1)- називається різницевим рівнянням першого порядку,є повною математичною моделлю ЛЦФ, що дозволяє по вхідній послідовності x(n) розрахувати вихідну і навпаки. Нехай a=2, y(0)=0. Для всіх n<0

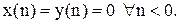
Тоді вихідна послідовність y(n):

n
x(n)
y(n)

Графіки вхідної і вихідної послідовностей

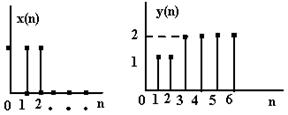Математичною моделлю ЛЦФ N-го порядку в загальному випадку є різницеве рівняння N-го порядку виду:

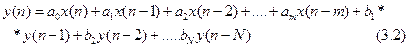
де M<=N, a_i, b_i- дійсні коефіцієнти.

Для перебування вихідної послідовності ЛЦФ y(n) необхідно знати вхідну послідовність x(n) і початкові умови y(-1),…..., y(-N).

( Це не значення вихідного сигналу, а саме початкові умови).

Класифікація ЛЦФ ґрунтується на обліку інформації про минулі стани системи.

Один із прикладів схемної реалізації зображений на рисунку:

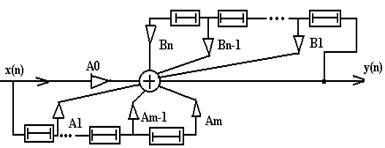Він зветься рекурсивний фільтр- від назви математичної операції- рекурсія-, що складається в циклічному звертанні до даних, отриманим на попередніх кроках.

Інший варіант ЛЦФ- трансверсальный фільтр (англ. “transverse”)- вхідні сигнали з затримкою і посиленням складаються в суматорi, щоб утворити вихідний сигнал.

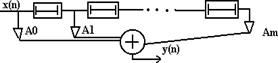Різницеве рівняння трансверсального фільтра:

y(n)=a₀x(n)+a₁x(n-1)+a₂x(n-2)+…+a_mx(n-m) (3.3)

a₀, a₁,…,a_m-дійсні коефіцієнти.

m- порядок трансверсального фільтра.

Функція його - зважене підсумовування попередніх отсчётов вхідного сигналу, не використовуючи минулі вiдлiки вхідного сигналу.

Фізично елемент затримки реалізується у виді регістра зрушення, перемножники – підсилювачем.

Рекурсивний фільтр має недолік – громіздку схему чи реалізацію, у випадку програмної реалізації вимагає великого обсягу пам'яті для збереження інформації окремо для рекурсивної і нерекурсивної частини. Більш досконалі - канонічні схеми рекурсивних цифрових фільтрів, у яких використовується мінімальна кількість елементів пам'яті P=max{N,M}.

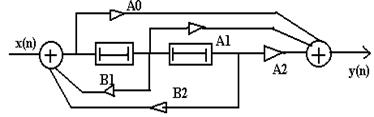Приклад: Схема рекурсивного фільтра 2-го порядку.

Методи аналізу ЛЦФ аналогічні методам аналізу лінійних аналогових кiл і є їх дискретними аналогами:

1) рішення різницевих рівнянь (аналог диф. рівнянь)

2) згортка з імпульсною характеристикою (аналог інтеграла накладення)

1) Z- перетворення (дискретний аналог перетворень Лапласа).

АНАЛІЗ ЛЦФ МЕТОДОМ РІШЕННЯ РІЗНИЦЕВИХ РІВНЯНЬ

полягає в простій підстановці вхідного сигналу в різницеве рівняння як повну модель ЛЦФ у прямому обчисленні по програмі (у випадку фільтрів великих порядків) вихідної послідовності.

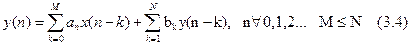
Приклад: нехай y(n)=x(n)-5y(n-1); початкові умови: y(-1)=0, x(n)=n+1

Пряма підстановка дає:

y(0)=x(0)-5y(-1)=1-5*0=1

y(1)=x(1)-5y(0)=2-5*1=-3

y(2)=x(2)-5y(1)=3-5*(-3)=18

y(3)=x(3)-5y(2)=4-5*18=-86

y(4)=x(4)-5y(3)=5-5*(-86)=475

Одержимо аналітичне рішення з різницею рівняння в явному виді. За аналогією з диф. рівнянням воно так само складається з загального і частккового рішень (із правою частиною - однорідного рівняння).

y(n)-5y(n-1)=0- однорідне рівняння. Рішення рівняння – вираження виду:

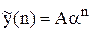
(за аналогією з ce^αt для диф. рівнянь 1-го порядку).

Приватні рішення, що відповідають вхідної послідовності x(n)=n+1, шукається у виді y^*(n)=An+B

Підставляючи обидва рішення по черзі в однорідне і неоднорідне рівняння і дорівнюючи коефіцієнти при рівних ступенях n, знаходять загальне рішення виду y(n)=n/a+b+A(-B)ⁿ, де a, b, A, B- числа.

Перевірка вираження для n=1, 2, 3,... дозволяє переконатися в повному збігу аналітичного рішення з безпосередньою прямою підстановкою.

Імпульсною характеристикою ЛЦФ g(n) називають відгук на δ- вхідну послідовність (за аналогією з аналоговими колами й аналоговими сигналами) при нульових умовах.

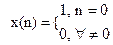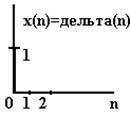Знайдемо ІX ЛЦФ 1-го порядку. Нехай

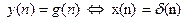Тоді

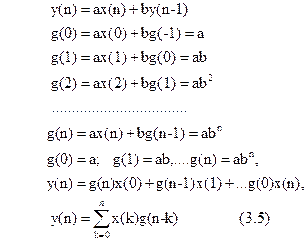Це дискретна згортка вхідної послідовності з імпульсною характеристикою.

АНАЛІЗ ЛЦФ МЕТОДОМ Z- ПЕРЕТВОРЕННЯ

При великих порядках фільтрів аналітичний розрахунок ЛЦФ у часовій області скрутний, як і у випадку аналогових ланцюгів.

У цьому випадку звертаються до дискретного аналізу перетворення Лапласа, а саме до Z- перетворення, що переводить аналіз в область комплексної дискретної частоти Z.

Будь-яку послідовність x(nΔt) можна представити у виді:

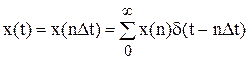
Застосуємо перетворення Лапласа до останнього рівняння:

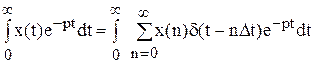
Перетворимо праву частину, виносячи за знак інтегралу незалежні від t величини:

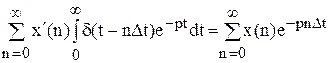
т.к. не власний інтеграл у теорії безупинних функцій дорівнює:

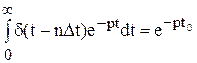
Уведемо позначення:

Розглянемо геометричну интерпретацию подібної заміни p→z

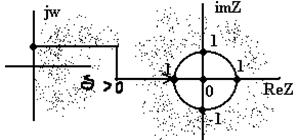Права напівплощина трансформується в зовнішню область окружності, ліва – у внутрішню, а ймовiрна вісь j – у саму окружність одиничного радіуса з центром у т. (0;0).

Т.о., будь-якiй дискретнiй послідовності x(n) можна поставити її пряме Z- перетворення:

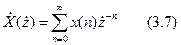
Приклад: Розглянемо дискретний сигнал x(n), знайдемо Z- перетворення

заданої послідовності по формулі (10.7);

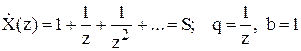
Воно є сумою геометричної прогресії зі знаменником <1 і сходиться при будь-яких z у кільці |z|>1. Підсумовуючи прогресію одержуємо:

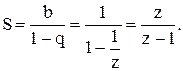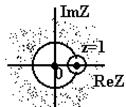На границі області аналiтичности ця функція має один простий полюс у т. z=1.

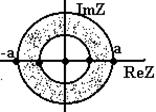Аналогічно виходить Z- перетворення нескінченного дискретного сигналу x(n)=(1, a, a²,…),де a – деяке дійсне число.

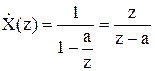По формулі (3.7) одержуємо область збіжності ряду – кільце |z|>a.

Представимо Z- перетворення довільної послідовності x(n) як розкладання в ряд Лорана функції X(z):

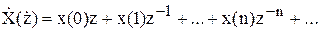
Чудова властивість Z- перетворення полягає в тім, що вихідна послідовність x(n) є відліковими коефіцієнтами цього ряду Лорана. Ми знаємо формулу визначення коефіцієнтів ряду Лорана як інтеграла по замкнутому контурі, рівного сумі відрахувань підінтегральної функції. Т.е. згадана властивість Z- перетворення дозволяє нам вирішити зворотню задачу: по Z- перетворенню відшукати саму вихідну послідовність x(n):