Кодирование с проверкой на четность

Широкое распространение в вычислительной технике получил метод контроля кодов по признаку четности-нечетности. Для этого метода выполняют суммирование цифр по модулю два, входящих в контролируемый код. Вместе с передаваемым кодом передается один контрольный разряд. Его значение (1 или 0) выбирается с условием, чтобы сумма цифр в передаваемом коде была по модулю два равна 0 для случая четности и 1 – для случая нечетности. При таком кодировании допускается, что может возникнуть только одна ошибка. Пример реализации метода четности представлен в таблице 2.3.

Таблица 2.3

Исходная комбинация	Контрольный разряд	Проверка
		1 – ошибка

Можно представить несколько измененный способ контроля по методу четности-нечетности. Длинное число разбивается на группы, каждая из которых содержит разрядов. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно схеме:

Увеличение избыточности передаваемых кодов приводит к тому, что появляется возможность не только обнаружить, но и исправить ошибку. Пусть произошла ошибка в одном из разрядов. Это приведет к тому, что при проверке на четность сумма по соответствующим строкам и столбцам изменится. Зафиксируется нарушение четности в строке и столбце, что означает обнаружение не только ошибки, но и ее места. Изменив содержимое отмеченного разряда на противоположное, исправляется ошибка.

Контроль по методу четности-нечетности широко используется для контроля записи, считывания информации в запоминающих устройствах на магнитных носителях, а также при выполнении арифметических операций.

Признаком отсутствия искажений в процессе приема-передачи является значение контрольного числа по методу проверки на четность равное нулю.

Кодирование с удвоением элементов

Данный метод кодирования характеризуется дополнительными символами для каждого информационного символа передаваемого кода. Информационная «1» представляется 10, а «0» 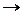01. Например, исходная комбинация 1011 преобразуется в 10011010. Показателем искажения являются сочетания типа 00 и 11 в «парных» элементах. Код не исправляет ошибки, приводящие к двукратным противоположным изменениямразрядов в парных элементах. Помехоустойчивость данного кода выше, чем кода с проверкой четности-нечетности, но при этом существенно возрастает избыточность кода.

Инверсное кодирование

В основе метода лежит повторение кодовой комбинации. Если исходная комбинация содержит четное число единиц, вторая, повторная комбинация в точности повторяет исходную. Иначе повторение происходит в инверсном виде. Например, комбинация 01010 в инверсном коде представляется как 0101001010; 11010 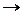1101000101. Проверка производится суммированием единиц основной комбинации. Если их число четно, то элементы второй части принимаются в том же виде. После чего обе части комбинации сравниваются поэлементно, т.е. первый элемент первой части с первым элементом второй части. При несовпадении хотя бы одного элемента принятая комбинация считается неверной.

Инверсный код позволяет обнаружить практически все ошибки приема-передачи. Не обнаруживаются лишь ошибки, где произошло одновременное искажение парных элементов в обеих частях комбинации.

Код Хемминга

Рассмотрим код Хемминга, исправляющий одиночные ошибки.

Код Хемминга, как и любой код содержит комбинацию m информационных и r = n-m избыточных символов. Избыточная часть кода строится так, чтобы при декодировании можно было установить не только наличие ошибки, но и ее положение. Это достигается путем многократной проверки принятой комбинации на четность, количество проверок равно значению избыточных символов r. При каждой проверке охватывается часть информационных символов и один из избыточных, при этом получают один контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение 0, если нечетное - 1. В результате всех проверок получается r - разрядное двоичное число, указывающее номер искаженного символа. Для исправления ошибки значение этого символа (бита) изменяется на обратное.

Необходимое количество проверочных символов r или значность кода для кодов Хемминга, исправляющих одиночные ошибки определяется из ранее полученного соотношения:

2^m £ 2ⁿ/(1+ n). (2.7)

Значения проверочных символов и номера их позиций по методу Хемминга устанавливается одновременно с выбором контролируемых групп кодовых комбинаций. При этом исходят из следующего: в результате первой проверки получают контрольное число, если оно равно 1, то один из символов первой проверенной группы искажен. Для выяснения вопроса, какой из символов может быть искажен, рассмотрим таблицу 2.4, в которой представлен натуральный ряд четырехразрядных контрольных чисел в двоичной системе счисления.

Таблица 2.4

№ п./п.	Символы разрядов контрольного числа
	(ст)			(мл)

Как видно из таблицы 2.4, если младший разряд контрольного числа содержит 1, то искажение должно быть в одной из нечетных позиций кодовой комбинации. Следовательно, первой проверкой должны быть охвачены символы с нечетными номерами. Если результат второй проверки даст 1, то получим 1 во втором разряде контрольного числа. Следовательно, второй проверкой должны быть охвачены символы с номерами, содержащими 1 во втором разряде двоичной записи этого номера: 2, 3, 6, 7, 10 и т.д. Аналогично при третьей проверке проверяться символы, номера которых в двоичной записи содержат 1 в третьем разряде: 4, 5, 6, 7, 12 и т.д.

Такие рассуждения позволяют образовать таблицу 2.5 проведения проверок.

Таблица 2.5

№ проверки	номера проверяемых позиций	номера позиций контрольных символов
	1,3,5,7,9,11,13... 2,3,6,7,10... 4,5,6,7,12... 8,9,10,11,12...

Если символы проверяемой кодовой комбинации обозначить через a_i, то проверочные суммы S_i можно записать следующим образом:

S₁ = а₁ а₃ а₅ а₇ а₉ .....

S₂ = а₂ а₃ а₆ а₇ а₁₀ .....

S₃ = а₄ а₅ а₆ а₇ а₁₂ .....

S₄ = а₈ а₉ а₁₀ а₁₁ а₁₂ .....

Номер позиции символа, в котором произошла ошибка в процессе приема-передачи комбинации, определяется следующим двоичным числом: N₂=....S_i....S₄ S₃ S₂ S₁.

С целью упрощения операций кодирования и декодирования целесообразно выбирать такое размещение проверочных символов в кодовой комбинации, при котором каждый из них включается в минимальное число проверяемых групп (лучше в одну группу). Нетрудно отметить из таблицы 2.4, что символы 1, 2, 4, 8......2ⁿ встречаются в каждой группе только один раз. Это связано с тем, что они являются степенью числа 2 и их двоичный код в таблице 4 содержит только одну единицу. Эти символы стоят на первом месте в правой части выражений для S_i. Таким образом, в коде Хемминга символы а₁, а₂, а₄, а₈.... должны быть проверочными, а символы а₃, а₅, а₇, а₉.... - информационными.

При передаче значения проверочных символов устанавливаются в кодовой комбинации такими, чтобы суммы S равнялись нулю (т.е. были бы четными числами), т.е. значения проверочных символов а₁, а₂, а₄.... выбираются из условия равенства S_i нулю.

Представим в качестве примера в коде Хемминга двоичную комбинацию 10010. Для нее число информационных символов m=5, при этом максимальное число передаваемых кодов равно 32. Разрядность кода Хемминга для m=5 должна быть равной 9 (n=9). Для девятиразрядного кода символы а₁, а₂, а₄ и а₈ являются проверочными, а символы а₃, а₅, а₆, а₇ и а₉ - информационными. Для заданного кода а₃=0, а₅=1, а₆=0, а₇=0 и а₉=1, тогда:

S₁ = а₁ 0 1 0 1 = а₁ 0=0, откуда следует, что а₁=0;

S₂ = а₂ 0 0 0 = а₂ 0=0, т.е. а₂ =0;

S₃ = а₄ 1 0 0 = а₄ 1=0, т.е. а₄ = 1.

Аналогично: а₈ = 1.

Следовательно, код Хемминга для кода 10010 будет равен 110011000.

Если при приеме-передаче произошла однократная ошибка в пятом символе, т.е. код при приеме принял значение 110001000, то в результате первой проверки будет получено число 1, в результате второй - 0, третьей - 1 и четвертой - 0. Таким образом, в результате проверок будет получено контрольное число 0101, указывающее на искажение пятого символа, принятой кодовой комбинации.

Если произойдет однократная ошибка приема-передачи первого символа кодовой комбинации, то сумма S₁ будет равна 1, а остальные суммы будут равны 0. Полученное контрольное число N будет равно 0001, что указывает на искажение первого символа принятого кода. Аналогичные контрольные числа будут получены при искажениях 2-го, 3-го и т.д. символов кода. Отметим, что для исправления ошибки принятой кодовой комбинации необходимо лишь изменить значение искаженного символа на противоположное.