Построение разверток поверхностей геометрических тел

Разверткой поверхности многогранника называют плоскую фигуру, полученную в результате последовательного совмеще­ния с плоскостью чертежа всех граней многогранника.

Рассмотрим построение разверток неко­торых простейших тел.

Начнем с наиболее характерного объема — куба (рис. 4). У куба все ребра и грани равны, боковая поверхность состоит из четырех равных квад­ратов, основания куба — два квадрата, тождественные квадратам боковой поверхности. Построим на листе развертку боковой поверхно­сти и граней основания. Затем по металлической линейке делаем над­резы глубиной примерно на 1/3 листа ватмана или тонкого картона. Затем развертку вырезаем. Для того чтобы собрать полученную раз­вертку при достаточной плотности бумаги, грани можно склеить встык друг с другом.

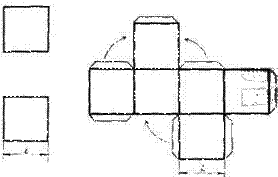Рис. 4

Однако при недостаточном опыте в макетировании лучше исполь­зовать следующий прием. На развертке у каждой грани куба делают отвороты краев, т.е. откладывают от каждой стороны полоски шири­ной 3—5 мм. Затем делают с наружной стороны надрезы макетным ножом по металлической линейке по линиям сгиба ребер. После этого вырезают развертку вместе с отворотами, осторожно сги­бают по ребрам и надрезанным отворотам, аккуратно смазывают от­гибы клеем ПВА и прижимают их к противоположенным граням. При достаточной аккуратности выполнения и точности вычерчивания раз­вертки макет получится качественным.

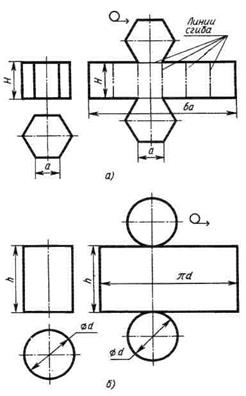
Развертка поверхности прямой призмы представляет собой плоскую фигуру, со­ставленную из боковых граней — прямо­угольников и двух равных между собой многоугольников оснований. Для примера взята правильная шестиугольная призма (рис. 5, а). Боковые грани призмы представляют собой равные между собой прямоугольники шириной а и высотой Н, а основания — правильные шестиугольни­ки со стороной, равной а. Так как разме­ры граней известны, построение развертки нетрудно выполнить. Для этого на гори­зонтальной прямой последовательно от­кладывают шесть отрезков, равных сторо­не основания а шестиугольника, т. е. 5а. Из полученных точек восстанавливают перпен­дикуляры длиной, равной высоте при­змы Н. Соединяя полученные отрезки, проводят вторую горизонтальную прямую. Полученный прямоугольник (Н/6а) яв­ляется разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуру оснований — два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сги­ба — штрихпунктирной тонкой с двумя точками.

С помощью подобного построения мож­но вычертить развертки прямых призм с любой фигурой в основании. Разница будет лишь в количестве и ширине граней боковой поверхности.

Аналогично строится и развертка повер­хности цилиндра (рис. 5, б). Только ши­рина ее равняется pd (длине окружности основания).

Развертка поверхности правильной пи­рамиды представляет собой плоскую фигу­ру, составленную из боковых граней — равнобедренных или равносторонних треу­гольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис. 6, а). Решение задачи осложняется тем, что не­известна величина боковых граней пира­миды, так как их ребра не параллельны ни одной из плоскостей проекций. Поэтому начинают построение с определения вели­чины ребра SA способом вращения (см. рис. 6, в). Определив длину на­клонного ребра SA, равную s'a¢₁, проводят из произвольной точки s, как из центра, дугу окружности радиусом s'a¢₁. По этой дуге откладывают четыре отрезка, равных стороне основания пирамиды, которое на чертеже спроецировалось в истинную ве­личину. Найденные точки соединяют пря­мыми с точкой s. Получив, таким образом, развертку боковой поверхности, пристраи­вают к основанию одного из треугольников квадрат, равный основанию пирамиды.

Развертка поверхности прямого круго­вого конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 6, б).

Построение выполняют следующим об­разом. Проводят осевую линию и из точки, взятой на ней, как из центра, очерчивают радиусом R₁, равным обра­зующей конуса s'a', дугу окружности. Затем подсчитывают угол сектора по формуле a = 360° × R/L, где R — радиус окружности основания конуса; L-длина образующей боковой поверхности конуса. В примере a = 360°× 15/38 = 142,2°.

Этот угол строят симметрично относи­тельно осевой линии с вершиной в точке S. К полученному сектору пристраивают круг с центром на осевой линии и диа­метром, равным диаметру основания конуса.

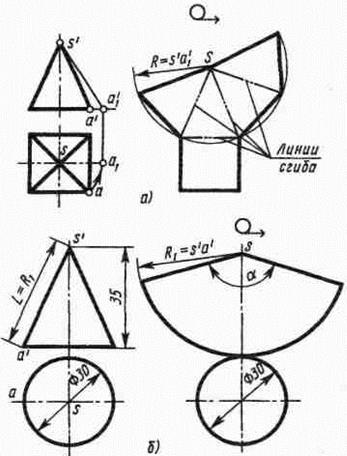
Рис. 6. Построение разверток поверхно­стей пирамиды и конуса