Порядковые и количественные натуральные числа. Счет

Учебно-методические материалы для КСР.

Тема. Понятие о натуральном числе и нуле. Отношения «равно», «меньше» на множестве целых неотрицательных чисел.

Цель:формирование у студентов представлений о теоретико-множественном подходе к понятию количественного натурального числа и нуля, совершенствование знаний студентов об отношениях «равно», «меньше» на множестве целых неотрицательных чисел.

Изучить материал темы по плану:

1. Порядковые и количественные натуральные числа. Счет.

2. Теоретико-множественный смысл количественного натурального числа и нуля.

3. Отношения «равно», «меньше» на множестве целых неотрицательных чисел.

Литература:

1. Кожух, I.Р. Матэматыка : Вучэб. дапам. для пед. ш-тау / I. Р. Кожух. — Мінск, Выш. шк., 1993. – с. – 89–90, 120–125.

2. Материалы лекции по теме «Понятие о натуральном числе и нуле. Отношения «равно», «меньше» на множестве целых неотрицательных чисел».

Вопросы для самоконтроля.

1. Какие числа называются натуральными? Как обозначается множество натуральных чисел?

2. Назовите основные правила счета элементов множества.

3. Что понимают под счетом элементов конечного множества?

4. Что называют отрезком натурального ряда чисел? Как он обозначается?

5. Дайте определение количественного натурального числа и нуля с позиций теории множеств.

6. Что называют множеством целых неотрицательных чисел? Как оно обозначается?

7. В чем разница между количественными и порядковыми натуральными числами?

8. Дайте определение отношения «равно» на множестве целых неотрицательных чисел.

9. Докажите, что отношение «равно» является отношением эквивалентности.

10. Дайте определение отношения «меньше» тремя способами:

а) связанное с теоретико-множественными понятиями;

б) связанное со сложением целых неотрицательных чисел;

в) исходя из понятия отрезка натурального ряда чисел.

11. Докажите, что отношение «меньше» на множестве целых неотрицательных чисел является отношением строгого линейного порядка.

Форма контроля:

– проверка конспектов изученного материала;

– экспресс-опрос студентов.

ТЕМА. Понятие о натуральном числе и нуле, отношениях «равно» и «меньше» на множестве целых неотрицательных чисел

1. Краткие исторические сведения о возникновении понятия натурального числа и нуля. Различные подходы к определению этих понятий.

2. Порядковые и количественные натуральные числа. Счет.

3. Понятие о натуральном числе как общем свойстве класса конечных равномощных множеств. Понятие о нуле.

4. Отношения «равно» и «меньше» на множестве Nο.

1. Краткие исторические сведения о возникновении понятия натурального числа и нуля. Различные подходы к определению этих понятий (реферат)

Порядковые и количественные натуральные числа. Счет

Натуральными называются числа, которые употребляются при счете предметов.

Проводя счет, мы соблюдаем ряд правил:

- первым при счете может быть указан любой элемент множества;

- ни один элемент множества не должен быть пропущен;

- нельзя считать элемент множества дважды.

А что представляет собой процесс счета?

Чтобы провести счет элементов множества А = {а, в, с, d} мы говорим: «первый», «второй», «третий», «четвертый». На этом процесс счета заканчивается, т.к. использованы все элементы множества А.

При счете элементов множества мы использовали порядковые натуральные числа. Сосчитав элементы множества А, мы говорим, что в множестве четыре элемента, т.е. получаем количественную характеристику элементов множества.

Отрезком N_а натурального ряда называют множество натуральных чисел, не превосходящих натурального числа а.

N_а = {х 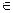| х N, х }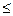

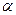N 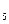= {1, 2, 3, 4, 5}

Счетом элементов множества А называется установление взаимно однозначного соответствия между множеством А и отрезком натурального ряда N_а.

а – число элементов в множестве А, n (А) = а

а – количественное натуральное число.