Прямая в пространстве
1) 
- общее уравнение прямой, как линии пересечения двух плоскостей, где 
и 
- нормальные векторы плоскостей 
и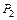 
.
2) 
- уравнение прямой, проходящей через точку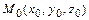 
параллельно вектору 
(каноническое уравнение);
3) 
- уравнение прямой, проходящей через две точки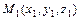 
, 
;
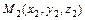4) 
-уравнение прямой, проходящей через точку 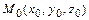параллельно вектору 
, 
(параметрическое уравнение);
Угол 
, ( 
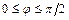) между прямым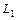и 
и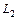 
: 
.
, если 
. 
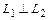, если 
.
Кривые на плоскости.
Алгебраическая кривая второго порядка: 
, где числа 
- не равны нулю одновременно.
Классификация кривых второго порядка:
1) если 
, то общее уравнение определяет кривую эллиптического типа (окружность (при 
), эллипс (при 
), пустое множество, точку);
2) если 
, то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых);
3) если 
, то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых) .
Окружность, эллипс, гипербола и парабола являются невырожденными кривыми второго порядка.
Окружность. Каноническое уравнение окружности: 
, где 
радиусокружности, точка 
-центрокружности.
Нормальное уравнение окружности: 
.Оно определяет окружность с центром в точке 
и радиусом 
.
Эллипс. Каноническое уравнение эллипса: 
, 
.
Числа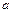 
и 
- большая и малая полуоси эллипса; точки 
, 
, 
, 
- вершины; оси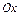 
и 
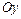- главные оси симметрии; точка - центр симметрии (или просто центр) эллипса; прямоугольник со сторонами 
, 
параллельными главным осям симметрии и центром в точке - основной прямоугольник эллипса; точки 
и 
, где 
- фокусы эллипса; векторы 
и 
- фокальные радиус-векторы; числа 
и 
- фокальные радиусы точки 
, принадлежащей эллипсу; число 
( 
) - эксцентриситетэллипса (при 
эллипс является окружностью); прямые 
и 
- директрисы эллипса.
Гипербола. Каноническое уравнение гиперболы 
, 
.
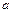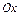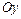Числа и - действительная и мнимая полуоси гиперболы; точки , - вершинами; оси и - главные оси симметрии; точка - центр симметрии (или просто центр) гиперболы; прямоугольник со сторонами , параллельными главным осям симметрии и центром в точке - основной прямоугольник гиперболы; точки и , где 
- фокусы гиперболы; векторы и - фокальные радиус-векторы; числа и - фокальные радиусы точки , принадлежащей гиперболе; число 
( 
) - эксцентриситетгиперболы; прямые 
и - директрисы гиперболы; прямые 
и 
называются асимптотами гиперболы (они проходят через противоположные вершины основного прямоугольника гиперболы).
Парабола. Каноническое уравнение параболы: 
, 
.
Число 
- параметр параболы; ось 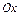- ось симметрии; точка – вершина параболы; точка 
- фокус параболы; вектор 
- фокальный радиус-вектор; число 
- фокальный радиус точки , принадлежащей параболе; прямая 
- директрисапараболы.
Поверхности.
Алгебраическая поверхность второго порядка: 
, где числа 
не равны нулю одновременно.
Сфера. Каноническое уравнение сферы: 
, где число -радиуссферы, точка 
- центр сферы.
Нормальное уравнение сферы: 
.Оно определяет сферу с центром в точке 
и радиусом .