Свойства векторного произведения
Системы линейных уравнений. Матричный
Метод.Правило Крамера. Метод Гаусса
Пусть задана система n линейных уравнений с n неизвестными вида
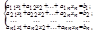 (4.1)
(4.1)
или, в матричной форме
А Х = В,
где
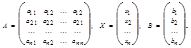
Формулы Крамера. Если система (4.1) невырождена, то она имеет единственное решение, определяемое формулами Крамера:
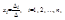
где 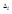 – определитель, получаемый из определителя
– определитель, получаемый из определителя 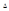 заменой его i-го столбца на столбец В свободных членов.
заменой его i-го столбца на столбец В свободных членов.
Матричный метод.
Решение невырожденной системы (4.1) можно найти по формуле 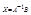 .
.
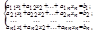
Метод последовательного исключения неизвестных (метод Гаусса).
С помощью элементарных преобразований над строками система m линейных уравнений с n неизвестными может быть приведена к виду
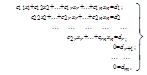 , (4.2)
, (4.2)
где 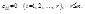
Система (4.2) эквивалентна исходной системе. Если хотя бы одно из чисел 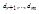 отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же
отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же 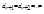
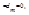 то система совместна и из уравнений (4.2) выражают последовательно неизвестны
то система совместна и из уравнений (4.2) выражают последовательно неизвестны 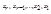 через
через 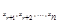 .
.
Скалярное произведение векторов в R3
Скалярным произведением векторов 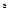 и
и 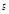 называется число, обозначаемое
называется число, обозначаемое 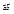 или
или 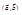 и равное
и равное 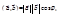 где
где 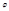 – угол между
– угол между 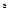 и
и 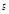 .
.
Свойства скалярного произведения:
1. 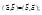 2.
2. 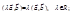
3. 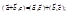 4.
4. 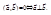
Свойство 4 выражает условие ортогональности векторов.
Если векторы 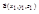 и
и 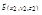 представлены своими координатами в ортонормированном базисе
представлены своими координатами в ортонормированном базисе 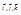 , то скалярное про-изведение равно
, то скалярное про-изведение равно 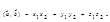 Из этой формулы и определения скалярного произведения следует:
Из этой формулы и определения скалярного произведения следует:
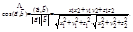
Учитывая, что 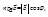 где
где 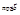 – проекция вектора
– проекция вектора 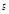 на вектор
на вектор 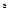 , а
, а 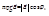 скалярное произведение векторов
скалярное произведение векторов 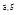 можно записать в виде
можно записать в виде
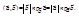
Механический смысл скалярного произведения: работа А, про-изводимая силой 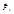 точка приложения которой перемещается из точки
точка приложения которой перемещается из точки 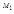 в точку
в точку 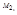 вычисляется по формуле
вычисляется по формуле
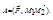
Векторное произведение векторов
Упорядоченная тройка некомпланарных векторов 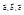 называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки; в противном случае тройка называется левой (рис. 4.1).
называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки; в противном случае тройка называется левой (рис. 4.1).

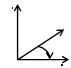
Рис. 4.1: а – тройка 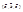 правая; б – тройка
правая; б – тройка 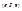 левая
левая
Векторным произведением вектора 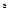 на вектор
на вектор 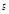 называется вектор
называется вектор  удовлетворяющий условиям:
удовлетворяющий условиям:
1) 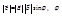 – угол между векторами
– угол между векторами 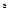 и
и 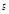 ;
;
2) 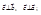
3) Упорядоченная тройка 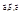 – правая.
– правая.
Обозначение: 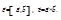
Свойства векторного произведения
1) 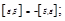
2) 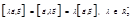
3) 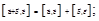
4) 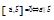 – условие коллинеарности векторов.
– условие коллинеарности векторов.
Если векторы 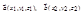 заданы своими коорди-натами в ортонормированном базисе
заданы своими коорди-натами в ортонормированном базисе 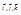 , то
, то
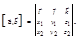
Площадь параллелограмма, построенного на векторах 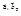 мож-но определить по формуле
мож-но определить по формуле
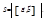
Механический смысл векторного произведения. Пусть точка А твердого тела закреплена, а в его точке В приложена сила 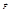 . Тогда возникает вращательный момент
. Тогда возникает вращательный момент 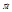 (момент силы). По определению момент силы относительно точки А находится по формуле
(момент силы). По определению момент силы относительно точки А находится по формуле 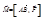 .
.
