Линейные операции над матрицами

Определитель ІІ порядка. Его свойства и вычисления

Определителем второго порядка соответствует матрице 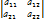называется число D равное D= .

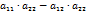Обозначается определитель так:

D=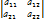

Элементы 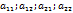матицы 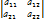называются элементами определителя D. Элементы 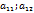составляют первую строку определителя D, соответственно 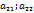это вторая строка. По аналогии 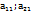первый столбец, 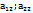второй столбец. Элементы 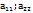главная диагональ, 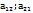побочная диагональ.

Правила определения определителя второго порядка:

Определитель второго порядка равен разности произведений элементов находящихся на главной диагонали и побочной.

Свойства определителя второго порядка:

· Определитель не изменится если его строки заменить столбцами и наоборот. То есть строки и столбцы равноправны.

· При перестановке двух столбцов (строк) определитель меняет знак на противоположный

· Определитель, имеющий два одинаковых столбца (строки) равен 0

· Если все элементы какой-либо строки определителя умножить на одно и то же число, то определитель умножится на это число. Замечание: ели все элементы любой строки содержат общий множитель, то его можно вынести за знак определителя

· Определитель, у которого элементы двух строк пропорциональны равен 0.

· Если каждый элемент любой строки определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей, у одного из них элементы соответствующей строки является первые слагаемые, а у другого вторые. Остальные элементы у этих определителей те же что у данного.

· Определитель не изменится если к элементам любой строки прибавить соответствующие элементы другой строки умноженные на одно и то же число.

Определитель ІІІпорядка. Правила его вычисления

Определителем третьего порядка соответствует матице есть число D равное алгебраической сумме произведений элементов матрицы. D=

Вычисление определителя третьего порядка:

· Правило треугольника: Со знаком + входят произведения элементов главной диагонали, а так же произведения элементов лежащих на параллелях к этой диагонали с добавлением третьего множителя из противоположного угла. А со знаком – входят произведения элементов побочной диагонали, а также произведения элементов лежащих на параллелях с добавлением третьего множителя из противоположного угла.

D= =

· Правило вычисления определителя третьего порядка путем разложения по элементам любой его строки или столбца на их алгебраические дополнения:

D= = + +

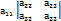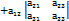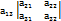
Линейные операции над матрицами

Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц Amxn=(a_ij) Bmxn=(b_ij) называется матрица Cmxn=(c_ij) такая, что c_ij=a_ij+b_ij (i=1,m, j=1,n)

Аналогично определяется разность матриц.

Произведение матрицы Amxn=(a_ij) на число k называется матрица у которой каждый элемент равен произведению соответствующего элемента матрицы Amxn=(a_ij) на число k. bij=k aij (i=1,m, j=1,n)

Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведение матрицы на матрицу называется матрица такая, что

c_ik=a_i1 b_1k+a_i2 b_2k+…+a_in b_nk. где (i=1,m, j=1,n)

т. е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-гo столбца матрицы В.

Замечание: в общем случае А