Первообразная и неопределенный интеграл

ДОПОВІДЬ

На тему: Первісна та невизначений інтеграл

Пiдготувала:

Скляревська Тетяна

Первообразная и неопределенный интеграл

Рассмотрим задачу: Дана функция f(x);требуется найти такую функцию F(x),производная которой равна f(x),т.е. F′ (x)= f(x).

Определение:1.Функция F(x) называется первообразной от функции f(x) на отрезке [a,b], если во всех точках этого отрезка выполняется равенство F′ (x)= f(x).

Пример. Найти первообразную от функции f(x)=x2.Из определения первообразной следует, что функция F(x)=х3/3 является первообразной, так как (х3/3)′= x2 .

Легко видеть, что если для данной функции f(x) существует первообразная , то эта первообразная не является единственной. Так, в предыдущем примере можно было взять в качестве первообразных следующие функции:

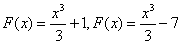, или вообще 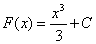(где С- произвольная постоянная), так как 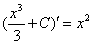. С другой стороны, можно доказать, что функциями вида 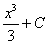исчерпываются все первообразные от функции x2 . Это вытекает из следующей теоремы.

Теорема. Если F1 (x) и F2 (х)- две первообразные от функции f(x) на отрезке [a,b], то разность между ними равна постоянному числу.

Доказательство. В силу определения первообразной имеем

F1 ′(х)= f(x), F2 ′(х)= f(x) (1)

При любом значении х на отрезке [a,b].

Обозначим

F1 (х)- F2 (х) =φ(х). (2)

Тогда на основании равенств (1) будет F′1 (х)- F′2 (х)= f(x)- f(x)=0 или φ′(х)=[ F′1 (х)- F′2 (х)]′≡0 при любом значении х на отрезке [a,b]. Но из равенства φ′(х)=0 следует, что φ(х) есть постоянная. Действительно, применим теорему Лагранжа к функции φ(х), которая, очевидно, непрерывна и дифференцируема на отрезке [a,b]. Какова бы ни была точка х на отрезке [a,b], мы имеем в силу теоремы Лагранжа φ(х)- φ(а)= (х-а) φ′(z), где а < z < x.Так как φ′(z)=0, то φ(х)- φ(а)=0, или φ(х)= φ(а). (3)

Таким образом, функция φ(х) в любой точке х отрезка [a,b] сохраняет значение φ(а), а это значит, что функция φ(х) является постоянной на отрезке [a,b]. Обозначая постоянную φ(а) через С, из равенств (2) и (3) получаем F1 (х)- F2 (х) = С.

Из доказанной теоремы следует, что если для данной функции f(x) найдена какая- нибудь одна первообразная F(x), то любая другая первообразная для f(x) имеет вид F(x)+ С, где С = const/

Определение 2. Если функция F(x) является первообразной для f(x), то выражение F(x)+ С называется неопределенным интегралом от функции f(x) и обозначается ∫f(x)dx.Таким образом по определению, ∫ f(x)dx= F(x)+ С, если F′ (x)= f(x). При этом функцию f(x) называют подынтегральной функцией, f(x)dx- подынтегральным выражением, знак ∫- знаком интеграла.

Таким образом, неопределенный интеграл представляет собой семейство функций y= F(x)+ С.

С геометрической точки зрения неопределенный интеграл представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т. е. вдоль оси Оу.

Естественно возникает вопрос: для всякой ли функции f(x) существуют первообразные( а значит, и неопределенный интеграл)? Оказывается, что на для всякой. Заметим, однако, без доказательства, что если функция f(x) непрерывна на отрезке [a,b],то для этой функции существует первообразная ( а значит, и неопределенный интеграл).

Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x).

Заметим следующее: если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. Из определения 2 следует:

1.Производная от неопределенного интеграла равна подынтегральной функции, т.е.если F′ (x)= f(x), то и

(∫ f(x)dx)′= (F(x)+C)′=f(x). (4)

Последнее равенство нужно понимать в том смысле, что производная от любой первообразной равна подынтегральной функции.

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

d(∫f(x)dx)= f(x)dx. (5)

Это получается на основании формулы (4).

3. Неопределенного интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

∫dF(x)= F(x)+C.

Справедливость последнего равенства легко проверить дифференцированием (дифференциалы от обеих частей равенства равны dF(x)).

Таблица интегралов.

Прежде чем приступить к изложению методов интегрирования, приведем таблицу интегралов от простейших функций.

1. 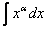= 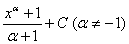.(Здесь и в последующих формулах под С понимается

произвольная постоянная.).

2. = .

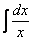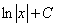3. =

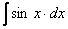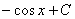
4. =

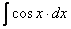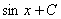
5. = .

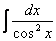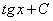6. = .

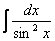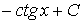7. = .

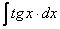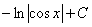8. = .

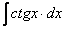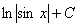9. = .

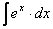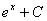10. =

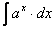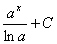
11. = .

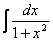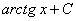11′. = .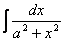

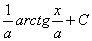12. = .

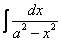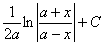13. = .

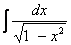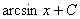13′ = .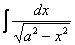

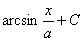14. = .

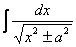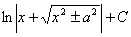Справедливость формул 7,8,11′,12,13′и 14 легко устанавливается с помощью дифференцирования.

В случае формулы 7 имеем ′= ,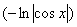

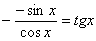следовательно, .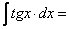

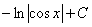В случае формулы 8

′= ,

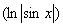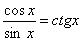следовательно, = .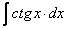

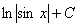В случае формулы 12

′= ,

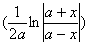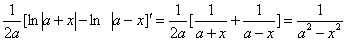следовательно, = .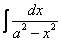

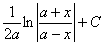В случае формулы 14

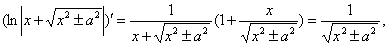
следовательно, = .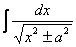

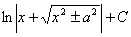3). Некоторые свойства неопределенного интеграла

Теорема 1.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:

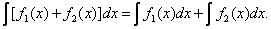(1)

Из доказательства найдем производные от левой и правой частей этого равенства. На основании равенства (4) пункта №1 находим

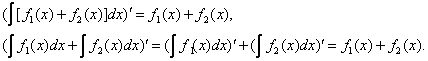
Таким образом, производные от левой и правой частей равенства (1) равны между собой, т. е. производная от любой первообразной, стоящая в левой части, равняется производной от любой функции, стоящей в правой части равенства. Следовательно по теореме из пункта №1 любая функция, стоящая в левой части равенства (1), отличается от любой функции, стоящей в правой части равенства(1), на постоянное слагаемое. В этом смысле и нужно понимать равенство (1).

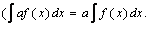Теорема 2. Постоянный множитель можно выносить за знак интеграла, т. е. если a=const, то

(2)

Для доказательства равенства (2) найдем производные от левой и правой его частей:

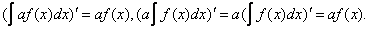
Производные от правой и левой частей равны, следовательно, как и в равенстве (1), разность двух любых функций, стоящих слева и справа, есть постоянная. В этом смысле и следует понимать равенство (2).

При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила.

1).Если

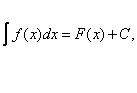
то

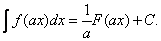(3)

Действительно, дифференцируя левую и правую части равенства (3) получим

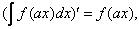
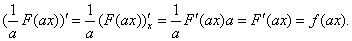Производные от правой и левой частей равны, что и требовалось доказать.

2). Если

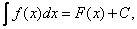
то

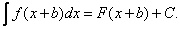(4)

3. Если

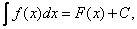
то

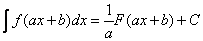. (5)

Равенства (4) и (5) доказываются дифференцированием правой и левой частей равенств.

Пример 1.

=

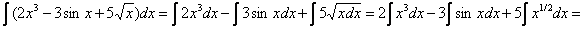
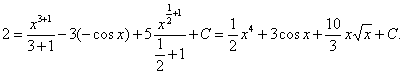
Пример 2.

=

=

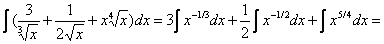
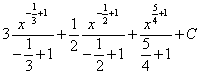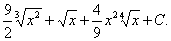
Пример 3.

.

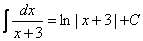Пример 4.

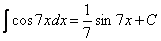
Пример 5.

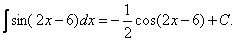
4)Интегрирование методом замены переменой или способом подстановки

Пусть требуется найти интеграл 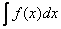, причем непосредственно подобрать первообразную для f(x) мы не сможем , но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении, положив

x=φ(t), (1)

где φ(t)-непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда dx= φ′(t)dt;докажем, что в этом случае имеет место следующее равенство:

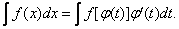(2)

Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х на основании равенства (1).

Для того чтобы установить, что выражения, стоящие справа и слева, одинаковы в указанном выше смысле, нужно доказать, что их производные по х равны между собой . Находим производную от левой части : 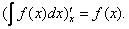Правую часть равенства (2) будем дифференцировать по х как сложную функцию, где t-промежуточный аргумент. Зависимость t от х выражается равенством (1), при этом 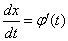и по правилу дифференцирования обратной функции .

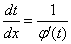Таким образом, имеем

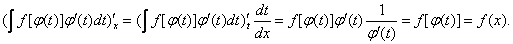
Следовательно, производные от х от право й и левой частей равенства (2) равны, что и требовалось доказать.

Функцию 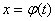следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).

Замечание. При интегрировании иногда целесообразнее подбирать замену переменной не в виде 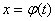, а в виде 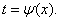Проиллюстрируем это на примере. Пусть нужно вычислить интеграл, имеющий вид

.

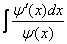Здесь удобно положить

,

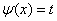тогда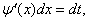

.

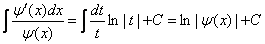Приведем несколько примеров на интегрирование с помощью замены переменных.

Пример 1.

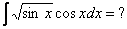Сделаем подстановку t=sin x; тогда dt= cosx dx и, следовательно,

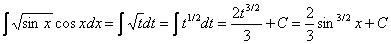
Пример 2.

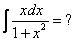Полагаем t=1+x2 ;тогда dt=2xdx и

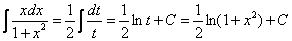
Пример 3.

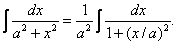Полагаем 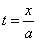; тогда dx=a dt,

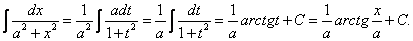
Пример 4. 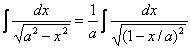. Полагаем 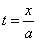; тогда dx=a dt,

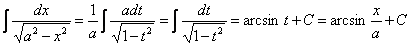
(предполагается, что a>0).

В примерах 3 и 4 выделены формулы ,приведенные в таблице интегралов под номерами 11′и 13′(см. выше,пункт №2).

Пример 5. 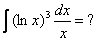Полагаем t=lnx; тогда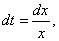

.

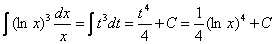Пример 6. 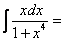? Полагаем 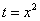;тогда dt= 2xdx,

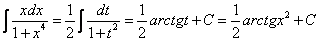
Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким -либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. По существу говоря изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения. Этому посвящены большая часть настоящего пункта.

5)Интегрирование по частям

Пусть u и v две дифференцируемые функции от х. Тогда, как известно, дифференциал произведения uv вычисляется по следующей формуле :d(uv)=udv+vdu.Отсюда, интегрируя, получаем 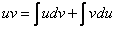или

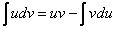. (1)

Последняя формула называется формула интегрирования по частям. Эта формула чаще всего применяется к интегрированию выражений которые можно так представить в виде произведения двух сомножителей u и dv, чтобы отыскать функцию v по её дифференциалу dv и вычисления интеграла 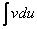составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла 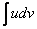. Умение разбивать разумным образом данное подынтегральное выражение на множители u и dv вырабатывается в процессе решения задачи , и мы покажем на ряде примеров, как это делается.

Пример 1. 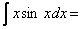? Положим u=x,dv=sinxdx;тогда du=dx,v= -cosx.Следовательно,

.

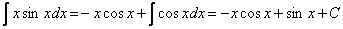Замечание. При определении функции v по дифференциалу dv мы можем брать любую произвольную постоянную, так как в конечный результат она не входит (что легко проверить, подставив в равенство(1) вместо v выражение v+C). Поэтому удобно считать эту постоянную равной нулю.

Правило интегрирования по частям применяется во многих случаях. Так, например, интегралы вида

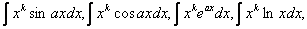
некоторые интегралы, содержащие обратные тригонометрические функции, вычисляются с помощью интегрирования по частям.

Пример 2. Требуется вычислить 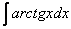. Положим u= arctg x, dv=dx;тогда 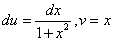. Следовательно,

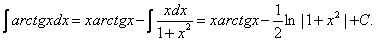
Пример 3. Требуется вычислить 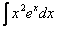. Положим 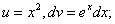тогда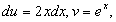

.

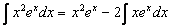Последний интеграл снова интегрируем по частям, полагая

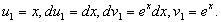Тогда

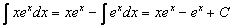. Окончательно будем иметь

.

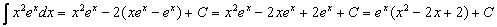Рациональные дроби. Простейшие рациональные дроби и их интегрирование

Как мы увидим ниже, далеко не всякая элементарная функция имеет интеграл, выражающийся в элементарных функциях. Поэтому очень важно выделить такие классы функций , интегралы которых выражаются через элементарные функции. Простейшим из этих классов является класс рациональных функций.

Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:

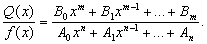
Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней.

Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.

Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:

;
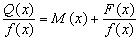