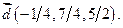Базис декартова прямоугольной системы координат
Единичный вектор 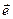 , т.е. вектор длины 1, определяет числовую ось
, т.е. вектор длины 1, определяет числовую ось 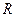 , начало которой совмещено с началом вектора
, начало которой совмещено с началом вектора 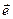 , а числу 1 соответствует конец вектора. Он называется базисным вектором оси.
, а числу 1 соответствует конец вектора. Он называется базисным вектором оси.
Пусть 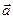 - произвольный вектор, коллинеарный базисному вектору. Отложив вектор
- произвольный вектор, коллинеарный базисному вектору. Отложив вектор 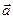 от начала оси, получим действительное число
от начала оси, получим действительное число 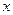 , определяемое на числовой оси концом отложенного вектора. Это число называется координатой вектора. Имеем
, определяемое на числовой оси концом отложенного вектора. Это число называется координатой вектора. Имеем
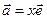 .
.
На координатной плоскости имеются два базисных вектора: на оси абсцисс, обозначаемый через 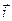 , и на оси ординат, обозначаемый через
, и на оси ординат, обозначаемый через 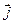 .
.
Пусть 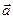 - произвольный вектор на плоскости. Отложив вектор
- произвольный вектор на плоскости. Отложив вектор 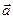 от начала координат мы однозначно определим упорядоченную пару действительных чисел
от начала координат мы однозначно определим упорядоченную пару действительных чисел 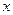 и
и 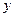 - координат конца
- координат конца 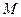 отложенного вектора. Эти числа называются координатами вектора
отложенного вектора. Эти числа называются координатами вектора 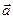 относительно базиса
относительно базиса 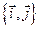 .
.
Так как 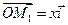 ,
, 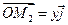 ,
, 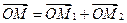 то
то 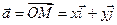 .
.
В координатном пространстве - три базисных вектора: 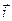 - на оси абсцисс,
- на оси абсцисс, 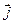 - на оси ординат,
- на оси ординат, 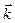 - на оси аппликат. Пусть
- на оси аппликат. Пусть 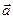 - произвольный вектор в пространстве. Отложив вектор
- произвольный вектор в пространстве. Отложив вектор 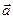 от начала координат, мы получим упорядоченную тройку чисел
от начала координат, мы получим упорядоченную тройку чисел 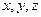 - координаты конца М отложенного вектора. Эти числа называются координатами вектора
- координаты конца М отложенного вектора. Эти числа называются координатами вектора 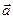 относительно базиса
относительно базиса 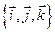 . Так как
. Так как
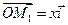 ,
, 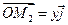 ,
, 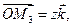
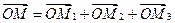
то
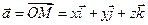 .
.
Замечание. Вектор 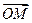 с началом в начале координат и концом в точке М (прямой, плоскости, пространства) называется радиус-вектором точки М. Таким образом, декартовыми координатами вектора
с началом в начале координат и концом в точке М (прямой, плоскости, пространства) называется радиус-вектором точки М. Таким образом, декартовыми координатами вектора 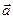 относительно данной системы координат называются координаты конца равного этому вектору радиус-вектора.
относительно данной системы координат называются координаты конца равного этому вектору радиус-вектора.
Из определения координат вектора непосредственно следует, что 1) при сложении векторов их соответствующие координаты складываются, 2) при умножении вектора на число каждая координата умножается на это число. В частности, справедлива формула:
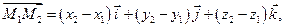
утверждающая, что вектор, определяемый двумя заданными точками 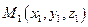 и
и 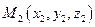 равен разности радиус- вектора конца и радиус-вектора начала, т.е. для вектора
равен разности радиус- вектора конца и радиус-вектора начала, т.е. для вектора 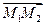 справедливо правило: «конец минус начало»
справедливо правило: «конец минус начало»
Если на прямой даны три точки 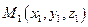 ,
, 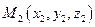 и
и 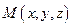 , причем
, причем 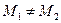 и справедливо векторное равенство:
и справедливо векторное равенство:
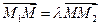
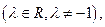
то говорят, что точка М делит отрезок 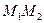 в отношении l. Причём
в отношении l. Причём
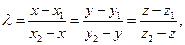
откуда находим:
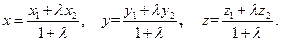
Полагая 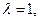 получим координаты середины отрезка
получим координаты середины отрезка 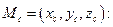
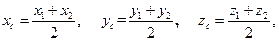
т.е. они равны полусуммам соответствующих координат его концов.
Пример. Даны векторы 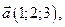
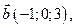
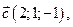 и
и 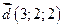 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 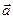 ,
, 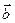 и
и 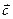 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 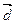 в этом базисе.
в этом базисе.
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
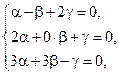
линейно независимы.
Тогда 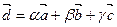 . Это условие выполняется, если определитель матрицы системы отличен от нуля.
. Это условие выполняется, если определитель матрицы системы отличен от нуля.
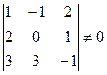 ;
;
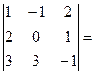
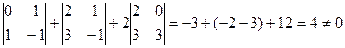 ;
;
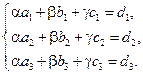
Для решения этой системы воспользуемся методом Крамера.
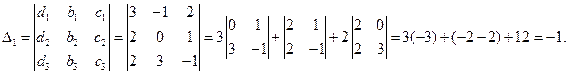
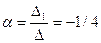 ;
;
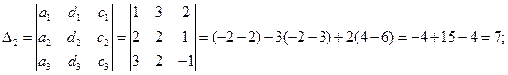
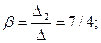
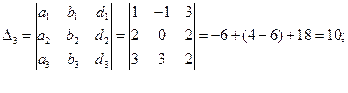
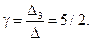
Следовательно, координаты вектора 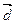 в базисе
в базисе 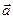 ,
, 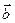 ,
, 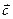 :
: