Смешанное произведение трех векторов
Рассмотрим три вектора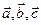 
. Их можно перемножить между собой различными способами:
1. 
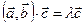- вектор, коллинеарный вектору 
.
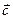2. 
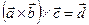- двойное векторное произведение.
3. 
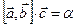- скаляр (векторно-скалярное произведение)
Смешанным произведением трех векторов 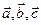(взятых в указанном порядке) называется скалярное произведение вектора 
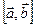на вектор .
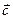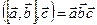- число!
Геометрический смысл смешанного произведения.
Смешанное произведение имеет простой геометрический смысл. Приведем векторы 
, 
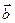и 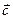к общему началу и построим на них параллелепипед; пусть 
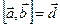. Тогда
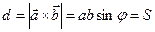
Полученный вектор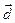 
умножим скалярно на :
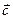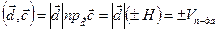
Но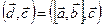 
; т.о.,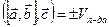 
Смешанное произведение трех векторов равно по модулю объему параллелепипеда, построенному на векторах , 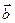и 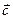. Знак этого произведения положителен, если тройка векторов , 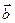и 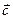расположена так же, как векторы 
, 
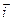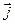и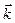 
, и отрицателен в противном случае.
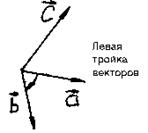
Упорядоченная тройка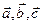 
некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. В противном случае тройка векторов – левая.
Если в данной тройке поменять местами любые два вектора, то характер ориентации изменится.
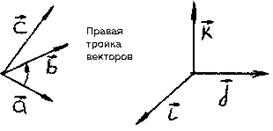
Замечание: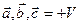 
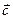если тройка правая ( и образуют острый угол) и 
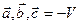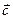, если тройка левая ( и образуют тупой угол).
Свойства смешанного произведения.
1. При перестановке двух соседних множителей смешанное произведение изменяет знак на противоположный:
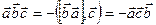
При перестановке соседних множителей местами объем параллелепипеда не изменяется, а изменяется характер ориентации тройки.
2. Смешанное произведение не изменяется при циклической перестановке сомножителей:
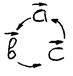
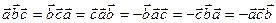
При этом не изменяется ни объем параллелепипеда, ни ориентация тройки векторов.
3. Смешанное произведение трех векторов равно нулю тогда и только тогда, когда эти векторы компланарны.
, ( 
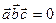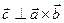, объем параллелепипеда равен нулю). Это необходимое и достаточное условие компланарности.
Смешанное произведение в координатной форме.
Пусть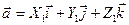 
; 
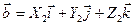и 
.
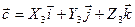Смешанное произведение трех векторов, взятых в определенном порядке, равно определителю 3 порядка, составленному из координат сомножителей, причем порядок строк соответствует порядку расположения сомножителей:
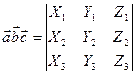
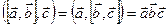
В смешанном произведении трех векторов важно сохранить последовательность записи векторов, но безразлично, где поставить знак векторного, а где скалярного произведения.
Условие компланарности трех векторов в координатной форме имеет вид:
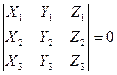
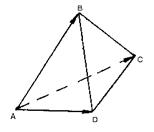Пример. Даны точки: A(-1,2,4); B(6,1,-3); C(4,5,-8) и D(4,2,1). Найти объем пирамиды.
, 
; 
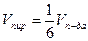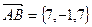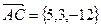и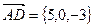 
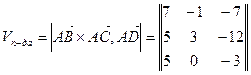
ЛЕКЦИЯ №4 Элементы аналитической геометрии.