Переходного процесса асинхронного ЭП в двигательном режиме

1.1 Построение естественной механической характеристики

1.1.1 Будем считать, что приводимый механизм создает на валу АД реактивный статический момент сопротивления постоянной величины: .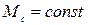

Чтобы иметь высокий КПД двигателя, выберем его нагрузку в пределах:

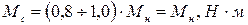, (1)

где: 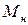– номинальный момент АД:

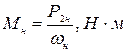, (2)

где: 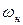– номинальная угловая частота вращения вала АД:

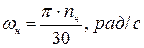, (3)

где: 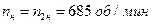– номинальная частота вращения вала АД

;

;

.

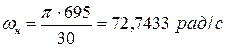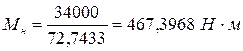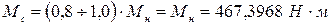1.1.2 Номинальное скольжение:

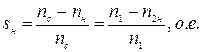, (4)

где: 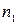– синхронная частота вращения магнитного поля статора АД:

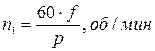, (5)

где: 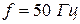– частота питающей сети;

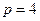– число пар полюсов АД;

;

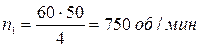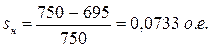
1.1.3 Рассчитаем естественную механическую характеристику АД по формуле Клосса:

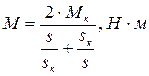, (6)

где: 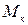– критическое (максимальное) значение момента, определяемое из отношения кратности критического момента:

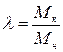; (7)

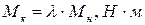; (8)

;

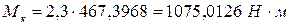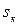– критическое скольжение:

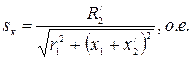, (9)

где: 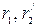– активное сопротивление фазы обмотки статора и приведенное к числу витков фазы статора активное сопротивление фазы обмотки ротора АД;

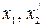– индуктивное сопротивление рассеяния фазы обмотки статора и приведенное к числу витков фазы статора индуктивное сопротивление рассеяния фазы обмотки ротора АД (в задании даны неприведенные значения параметров ротора 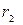и 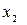и коэффициент приведения по ЭДС ):

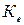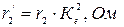; (10)

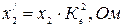; (11)

;

;

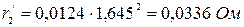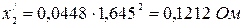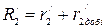– суммарное активное сопротивление фазы ротора АД, приведенное к числу витков фазы обмотки статора, включающее приведенное добавочное сопротивление фазы обмотки ротора 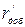(при построении естественной механической характеристики 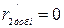), Ом;

.

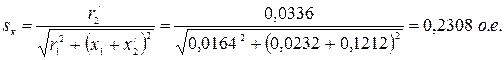
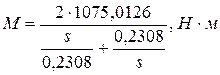Далее, задаваясь скольжениями в диапазоне 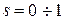(таблица № 3), по формуле Клосса строим естественную механическую характеристику АД, представленную на рисунке 3.

Таблица № 3. – Естественная и искусственные механические характеристики АД с фазным ротором

s		0,05	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5	0,55	0,6	0,65	0,7	0,75	0,8	0,85	0,9	0,95
М
М1 доб.1
М2 доб.2
М3 доб.3

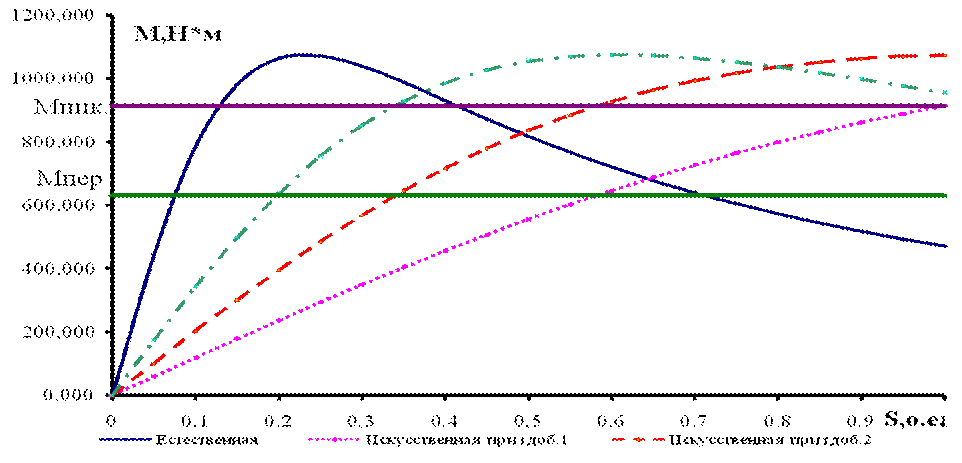Рисунок 3. – Естественная и искусственные механические характеристики АД с фазным ротором

1.2 Ступенчатый пуск АД с фазным ротором

1.2.1 Значение пускового момента АД:

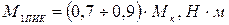; (12)

.

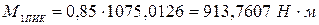1.2.2 Значение переключающего момента АД:

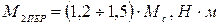; (13)

.

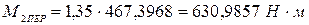1.2.3 Скольжение на естественной механической характеристике при :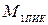

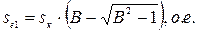, (14)

где: 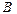– коэффициент кривизны естественной механической характеристики:

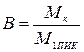; (15)

;

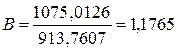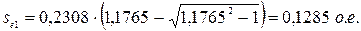
1.2.4 Задаемся количеством ступеней пускового реостата 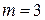. Обычно .

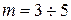1.2.5 Скольжение на естественной механической характеристике при :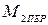

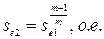; (16)

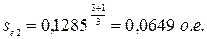
1.2.6 Подставляя в формулу Клосса 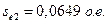, проверяем выполнение условия :

.

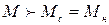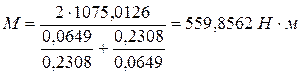Т.е. проверка верна, т.к. .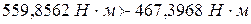

Так как метод расчета количества ступеней пуска приближенный, то возможны дефекты взаимного расположения искусственных характеристик: пусковая характеристика с добавочным сопротивлением 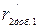не проходит через точку короткого замыкания ( 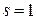) при моменте 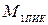(задано по условию пуска), переключение на очередную механическую характеристику проходит при моменте, отличающемся от 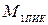. В этом случае необходимо откорректировать прохождение характеристик, подбирая приведенные значения добавочного сопротивления 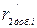. Добившись желаемого взаимного расположения всех искусственных механических характеристик АД, построим на одном графике с естественной скорректированные искусственные механические характеристики АД в диапазоне скольжений 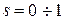(см. таблицу № 3 и рисунок 3).

Из построенных характеристик, помимо 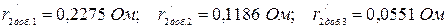и критических скольжений 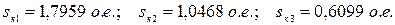, определим 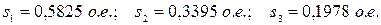, являющиеся 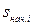и 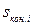для переходного процесса АД.

1.2.7 Приращение скольжений на каждой 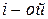ступени пуска :

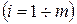- для первой ступени пуска:

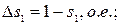(17)

;

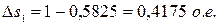- для второй ступени пуска:

(18)

;

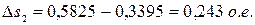- для третьей ступени пуска:

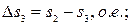(19)

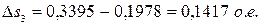
1.2.8 Добавочные (реальные) сопротивления пускового реостата для каждой 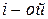ступени пуска:

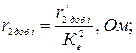(20)

- для первой ступени пуска:

;

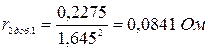- для второй ступени пуска:

;

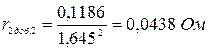- для третьей ступени пуска:

.

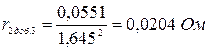1.2.9 Полное активное сопротивление роторной цепи:

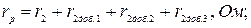
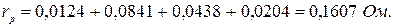
1.2.10 Изменение скольжения в процессе пуска при изменении времени для различных ступеней пускового реостата:

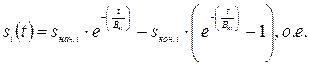, (21)

где: 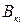– коэффициент кривизны соответствующей механической характеристики АД:

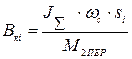, (22)

где: – суммарный момент инерции, приведенный к валу двигателя:

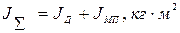, (23)

где: 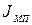– момент инерции механизма, приведенный к валу АД:

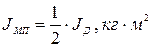; (24)

;

;

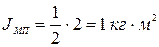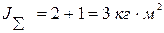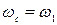– синхронная угловая частота вращения АД:

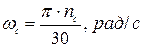; (25)

;

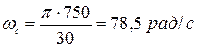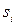– скольжение при моменте 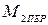на 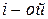механической характеристике:

;

;

;

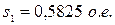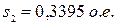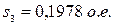- для первой ступени пуска:

;

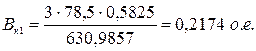- для второй ступени пуска:

;

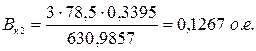- для третьей ступени пуска:

;

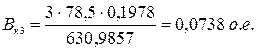- для первой ступени пуска:

;

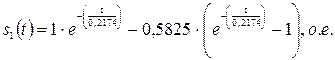- для второй ступени пуска:

;

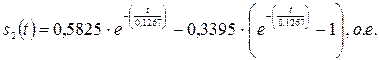- для третьей ступени пуска:

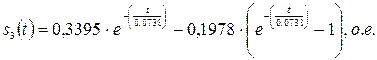
Изменяя время 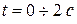для трех ступеней разгона, строим зависимость 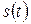переходного процесса АД с фазным ротором, причем момент времени окончания переходного процесса на предыдущей ступени разгона является моментом времени начала переходного процесса следующей ступени. Данные расчета представлены в таблице № 4, а характеристика переходного процесса приведена на рисунке 4.

Далее строим зависимость 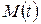переходного процесса АД, величину которой получаем подстановкой значений 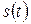в формулу Клосса. Данные сводим в таблицу № 5, а характеристика переходного процесса показана на рисунке 5.

Таблица 4. – Переходной процесс АД с фазным ротором, зависимость s(t)

t, c		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
s, о.е.		0,8460	0,7488	0,6875	0,6488	0,6243	0,6089	0,5991	0,5930	0,5891	0,5866
t, c	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
s, о.е.	0,5851	0,5841	0,5835	0,3395	0,3395	0,3395	0,3395	0,1978	0,1978	0,1978

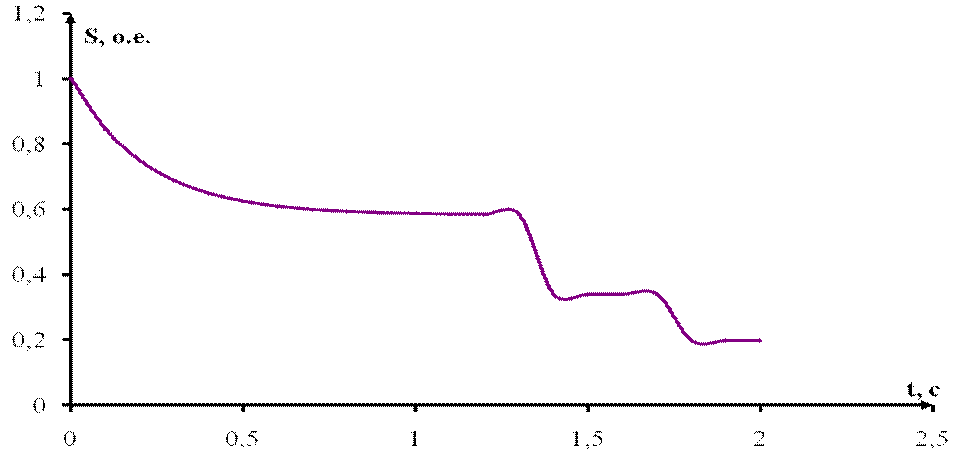
Рисунок 4. – Переходной процесс АД с фазным ротором, зависимость s(t)

Таблица № 5. – Переходной процесс АД с фазным ротором, зависимость М(t)

t,c		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9		1,1
М,Н*н	913,84	828,92	763,75	717,89	687,07	666,87	653,83	645,48	640,16	636,79	634,65	633,3
t,c	1,2	1,3	1,3	1,4	1,5	1,6	1,7	1,7	1,8	1,9
М,Н*н	632,44	631,9	914,4	630,94	630,93	630,93	630,93	913,69	630,92	630,92	630,92

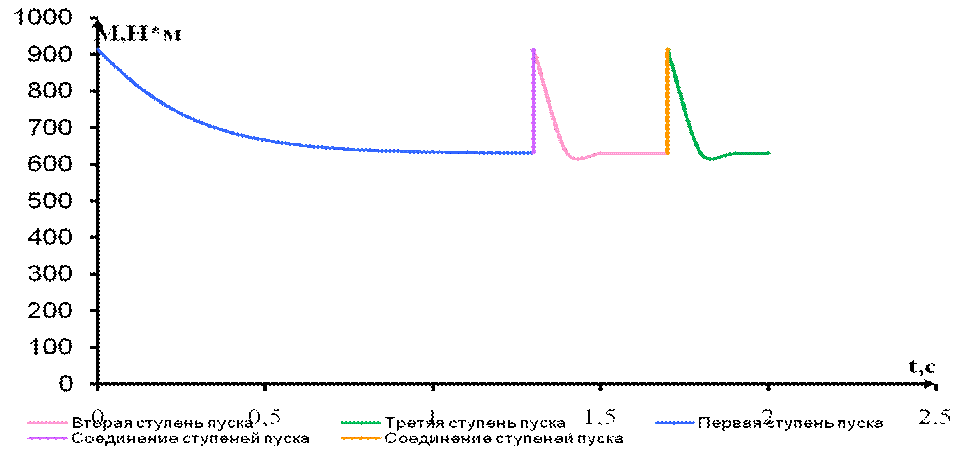Рисунок 5. – Переходной процесс АД с фазным ротором, зависимость М(t)