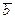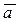Линейные операции над векторами

Под линейными операциями над векторами понимают операции сложения и умножение вектора на число.

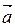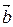Суммой двух векторов и называется вектор 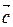, соединяющий начало вектора 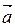с концом вектора 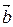, отложенного от конца вектора 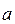. Обозначается 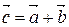. Для геометрического представления суммы векторов используют правила «треугольника» (рис.3) и «параллелограмма»

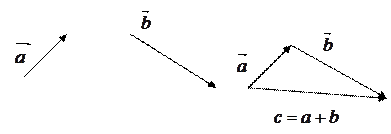(рис.4).

Рис. 3.

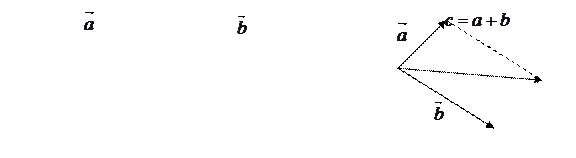
Рис. 4.

Под разностью векторов 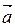и 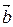понимается вектор 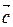такой, что 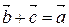. Обозначение: .

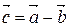Произведением вектора 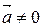на число 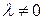называется вектор 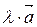, который имеет длину 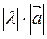,направление вектора 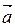, если 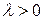и противоположное направление, если .

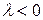Свойства линейных операций:

1) 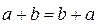(переместительный закон);

2) 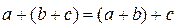(сочетательный закон сложения);

3) 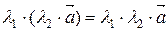(сочетательный закон умножения);

4) 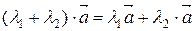(распределительный закон относительно сумы чисел);

5) 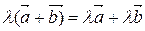(распределительный закон относительно суммы векторов).

4. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Скалярным произведением векторов 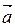и 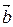называется число (скаляр), равное произведению длин этих векторов на косинус угла 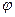между ними

= .

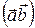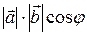(3)

Если хотя бы один из перемножаемых векторов нулевой, то угол неопределен и скалярное произведение по определению полагают равным нулю.

Свойства скалярного произведения:

1) 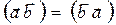(переместительный закон)

2) 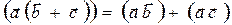(распределительный закон)

3) 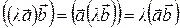(сочетательный закон по отношению к скалярному множителю)

4) 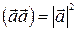-скалярный квадрат вектора, неотрицательное число, равное квадрату длины вектора.

5) 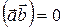, если 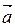=0,либо 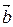=0,либо 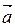перпендикулярен .

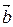Если векторы заданы координатами 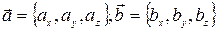, то скалярное произведение равно сумме парных произведений одноименных координат, то есть его удобно находить по формуле

.

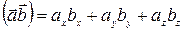(4)

Косинус угла между векторами

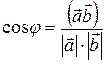(5)

Пример 2.Найти скалярное произведение векторов: 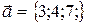и 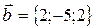и угол между ними.

Решение. Скалярное произведение находим по формуле (4):

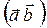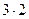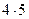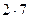= - + =6-20+14=0, значит, вектора перпендикулярны.

Пример 3.Найти скалярное произведение векторов 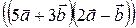, если .

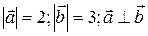Решение: .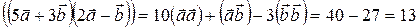

5. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Векторным произведением вектора 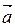на вектор 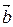называется третий вектор 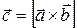, определяемый следующим образом (рис. 5):

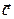
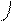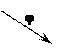Рис. 5.

1) модуль вектора 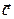равен произведению длин перемножаемых векторов на синус угла между ними

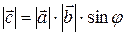(6)

2) вектор 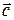перпендикулярен перемножаемым векторам 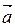и ;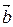

3) векторы 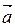, , 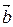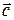после приведения к общему началу ориентированы по отношению друг к другу соответственно как орты i, j, k (в правой системе координат образуют так называемую правую тройку векторов).

Модуль векторного произведения равен площади параллелограмма, построенного на векторах 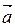и 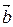как на сторонах.

Свойства векторного произведения:

1) 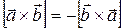то есть векторное произведение не обладает переместительным свойством;

2) 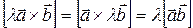(сочетательный закон по отношению к скалярному множителю);

3) 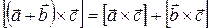(распределительный закон);

4) 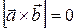, если 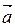= 0,либо 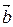= 0, либо вектора коллинеарны || .

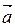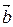Векторные произведения координатных ортов

;

.

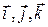
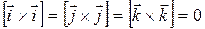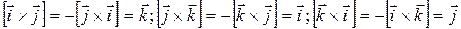Если векторы заданы координатами 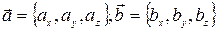, то ихвекторное произведение есть вектор, координаты которого получим, раскрыв по первой строке определитель третьего порядка, в первой строке которого орты 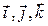, во второй и третьей – координаты перемножаемых векторов

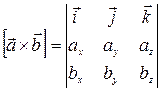(7)

Пример 4.Вычислить площадь параллелограмма, построенного на векторах .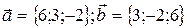

Решение. Найдем векторное произведение (7)

.

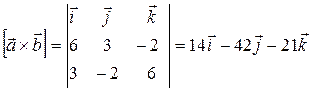Площадь параллелограмма равна модулю векторного произведения

S= 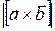= =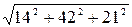49 (кв. ед).

6. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Смешанным произведением трех векторов 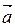, , 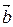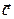называется число, равное скалярному произведению вектора 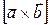на вектор 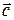: 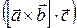. Свойства смешанного произведения

1) Смешанное произведение трех векторов равно нулю, если:

а) хотя бы один из перемножаемых векторов равен нулю;

б) два из перемножаемых векторов коллинеарны;

в) все три вектора параллельны одной и той же плоскости –компланарны.

2) Смешанное произведение не изменяется, если в нем поменять местами знаки векторного (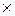) и скалярного (·) умножения, то есть

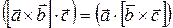.Поэтому смешанное произведение векторов 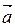, , 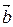, 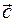записывают в виде.

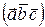3) Смешанное произведение не изменяется, если переставлять перемножаемые векторы в круговом порядке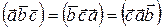

4) При перестановке любых двух векторов смешанное произведение изменяет знак: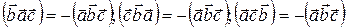

5) Модуль смешанного произведения трех векторов 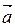, , 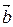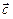равен объему параллелепипеда, построенного на этих векторах как на ребрах.

Если векторы заданы координатами

,

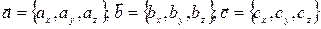то их смешанное произведение найдем, вычислив определитель третьего порядка, составленный построчно из координат перемножаемых векторов

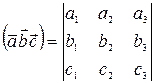(8)

Пример 5.Показать, что векторы 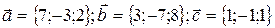компланарны.

Решение. Векторы компланарны, если их смешанное произведение равно нулю. Находим

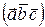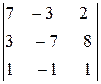= =-49-24-6+14+9+56=-79+79=0.

Условие выполнено – векторы компланарны.

Пример 6.Найти объем треугольной пирамиды с вершинами в точках 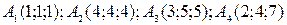, а также высоту из вершины .

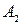Решение.

Объем пирамиды:

.

, .

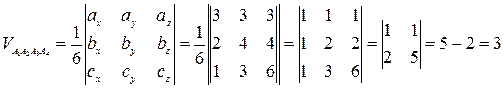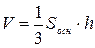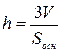Найдем площадь основания

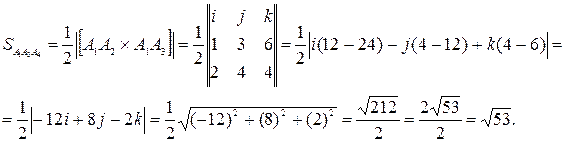
Высота, проведенная из вершины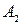

.

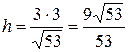7. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ

Векторы 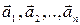называются линейно–зависимыми, если существуют такие числа 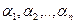, не все равные нулю, что их линейная комбинация

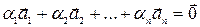(9)

и линейно независимыми, если это равенство выполняется только при всех 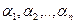равных нулю. Если среди векторов 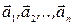есть нулевой вектор, то эти векторы линейно зависимы. Наличие линейной зависимости между векторами означает, что хотя бы один из них можно представить линейной комбинацией остальных.

Для того чтобы векторы 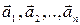были линейно независимы, необходимо и достаточно, чтобы ранг матрицы, составленной из координат этих векторов, r был равен числу векторов n. Если ранг матрицы меньше числа векторов 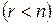, то векторы линейно зависимы.

Пример 7. Проверить, будут ли векторы

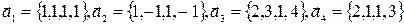линейно зависимы.

Решение. Составим матрицу из координат векторов и приведем ее к ступенчатому виду

.

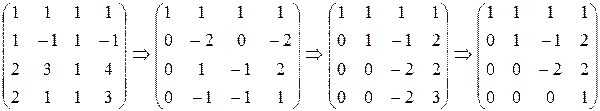Ранг матрицы равен четырем и равен числу векторов, следовательно они линейно независимы.

Заметим, что два коллинеарных на плоскости, как и три компланарных вектора в трехмерном пространстве линейно зависимы.

Пример 8. Определить, при каком значении параметра 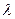векторы 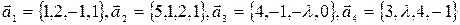будут линейно зависимы.

Решение. Поскольку количество векторов равно количеству координат этих векторов, матрица из них будет квадратной, и ее ранг будет меньше числа векторов, если определитель матрицы будет равен нулю. Тогда решим уравнение

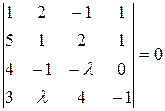, тогда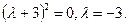

Чтобы установить линейную зависимость между векторами, надо разложить по столбцу равный нулю определитель, составленный из координат этих векторов.

Пример 9.Установить линейную зависимость между векторами

.

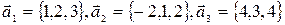Решение. Составим равный нулю определитель третьего порядка, строчками которого являются координаты данных векторов

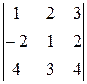=0

и раскроем его по элементам третьего столбца

.

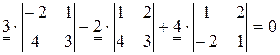Здесь подчеркнуты элементы столбца – представители соответствующих векторов, таким образом имеем линейную комбинацию 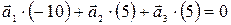, следовательно по (9) .

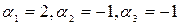8. БАЗИС. РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА

Любой упорядоченный набор из n действительных чисел 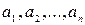называется n-мерным вектором 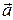; при этом указанные числа называются координатами вектора 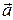. Совокупность всех n-мерных векторов называется n-мерным векторным пространством .

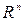В n-мерном векторном пространстве 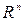максимальное число линейно независимых векторов равно n , именно оно и называется размерностью векторного пространства.

Пример 10.Определить размерность пространства векторов .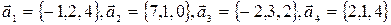

Решение. Составим матрицу из координат векторов и подсчитаем ее ранг, приведением к ступенчатому виду

,

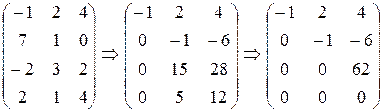из чего следует, что только три вектора являются линейно независимыми, и размерность пространства равна трем.

Базисом векторного n-мерного пространства называют любую совокупность, состоящую из n линейно независимых векторов этого пространства (заданных в определенном порядке). Таким образом число векторов базиса совпадает с размерностью пространства. В n-мерном пространстве можно подобрать бесчисленное множество различных базисов. Всякий вектор 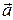n-мерного пространства единственным образом может быть представлен линейной комбинацией векторов его базиса – разложен по базису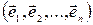

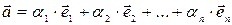(10)

Пример 11.Разложить вектор 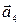по базису, образованному векторами 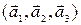(см. пример 10).

Решение. Проверим, действительно ли векторы 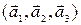образуют базис. Для этого составим определитель третьего порядка из их координат и убедимся, что он отличен от нуля

.

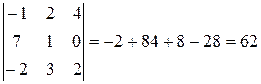Составим определитель четвертого порядка из координат векторов 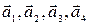, добавив первый столбец, по которому и раскроем равный нулю определитель

,

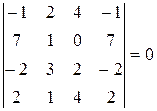получим равенство 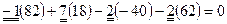, из которого имеем искомое разложение

.

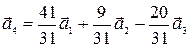Базис называется ортогональным, если каждый его вектор ортогонален остальным векторам базиса (скалярное произведение любых двух векторов – сумма парных произведений их координат – равно нулю). Если все векторы ортогонального базиса имеют единичную длину, то базис называется ортонормированным. Примером такого базиса является декартов ортогональный базис 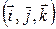. Найти координаты вектора в таком базисе можно, используя скалярное произведение, то есть по формуле

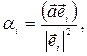i=1,2,…,n.

(11)

Пример 12. Найти координаты вектора 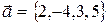в ортогональном базисе, состоящем из векторов .

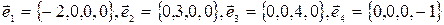Решение. Найдем квадраты длин базисных векторов

.

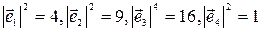По формулам (11) вычислим координаты вектора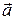

.

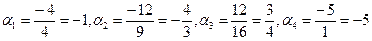Получено разложение вектора по ортогональному базису

.

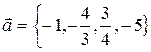9. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ

Пусть вектору 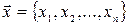из n-мерного векторного пространства 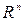по некоторому правилу ставится в соответствие вполне определенный вектор 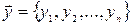из 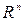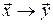. Это соответствие называется преобразованием векторного пространства и обозначается

,

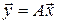(12)

где А – оператор преобразования, переводящего прообраз - 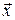в образ - 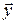. Всякое линейное преобразование – оператор А может быть задано соответствующей матрицей преобразования А и записано в виде матричного уравнения (12) или системы уравнений

.

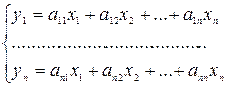(13)

Если матрица А невырожденная, то и оператор А невырожденный, и тогда существует обратноепреобразование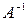

,

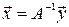(14)

которое получим, если слева умножим вектор 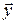на обратную матрицу .

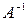Пример 13.Дано линейное преобразование

.

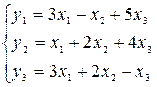Найти преобразование, переводящее вектор 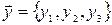в вектор .

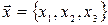Решение. Данное преобразование 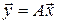прямое, где

.

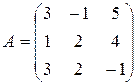Искомое преобразование - обратное 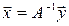, осуществляет его матрица, обратная матрице А. Поскольку определитель матрицы А равен -63, то для нее существует обратная

,

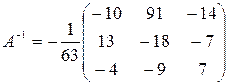тогда искомое преобразование

.

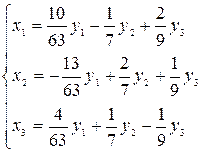Поскольку линейное преобразование полностью характеризуется его матрицей, то действия над такими преобразованиями сводятся к действиям над их матрицами.

Пример 14.Даны два линейных преобразования

.

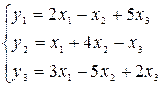
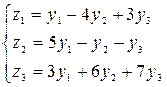Найти преобразование, переводящее вектор 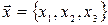в вектор .

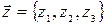Решение. Первое преобразование определяется матрицей

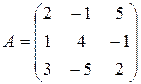
и переводит вектор 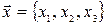в вектор 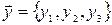: 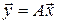. Второе преобразование определяется матрицей

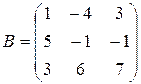
и переводит вектор в вектор 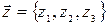: 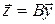. Искомое преобразование осуществляется произведением 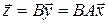. Перемножим матрицы в указанном порядке

.

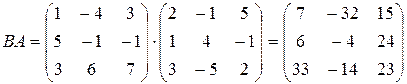Искомое преобразование осуществляется матрицей

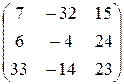
и может быть записано в виде системы уравнений

.

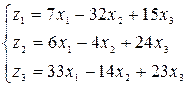10. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЧИСЛА ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ

Вектор называется собственным вектором данного линейного преобразования, если для этого вектора имеет место равенство 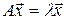, где 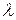- собственные числа вектора .

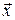Чтобы найти собственные числа матрицы А, составляют характеристическое уравнение 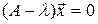, то есть

,

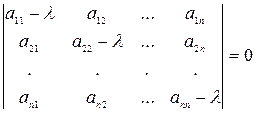корни которого и есть собственные числа.

Чтобы найти собственный вектор 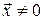, для каждого собственного числа составляют систему уравнений вида

.

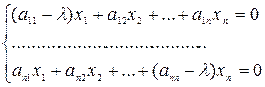Поскольку эта система нетривиально совместна, то ее ненулевое решение и будет собственный вектор. Заметим, что собственные векторы определяются неоднозначно, а с точностью до произвольного постоянного множителя с.

Пример 15. Найти собственные числа и собственные векторы линейного преобразование, заданного матрицей .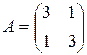

Решение. Составим характеристическое уравнение

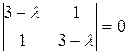
и найдем его корни - собственные числа 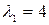; 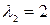. Для каждого собственного числа составим однородные системы уравнений

для ;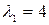

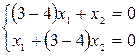для .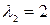

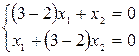Из которых следует, соответственно 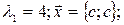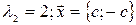, где с - произвольная константа.