Переходные характеристики формирующих двухполюсников
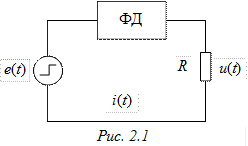
Определим свойства ФД при воздействии на него перепада напряжения (единичной ступенчатой функции ЭДС) для случая формирования импульса прямоугольной формы, длительность которого равна t, а амплитуда равна I. Схема такого устройства должна представлять собой последовательное соединение нагрузки R, источника перепада напряжения e(t) и самого ФД (рис. 2.1) [2], [3]. Преобразованная функция для прямоугольного импульса
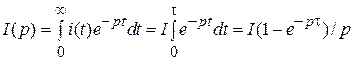 . (2.1)
. (2.1)
Операционное уравнение для цепи (рис. 2.1) может быть записано в виде
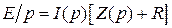 , (2.2)
, (2.2)
где E – перепад ЭДС источника; Z(p) – операционное сопротивление ФД.
Решив (2.2) с учетом (2.1), получим
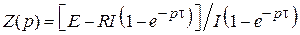 . (2.3)
. (2.3)
Найдем переходную функцию ФД, которая в данном случае является переходной проводимостью h(t), под которой понимается ток, вызываемый единичным перепадом напряжения на зажимах ФД (рис. 2.2).
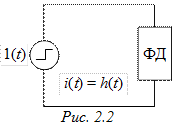
Преобразованная функция H(p) переходной проводимости h(t):
H(p) = 1/pZ(p).
Подставив в эту зависимость значения из (2.3), получим
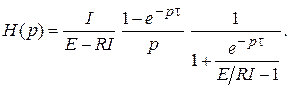 (2.4)
(2.4)
Последняя дробь в формуле (2.4) может быть представлена в виде геометрической прогрессии
1/(1 + a) = 1 – a + a2– a3 + a4– ... .
Поэтому выражение для H(p) можно записать в виде следующего бесконечного ряда:
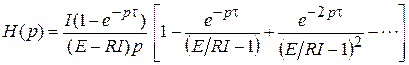 . (2.5)
. (2.5)
Для нахождения переходной проводимости ФД необходимо произвести обратное преобразование. Из рассмотрения преобразованной функции (2.5) видно, что переходная проводимость h(t) будет определяться также бесконечным рядом, члены которого могут быть найдены почленным обратным преобразованием. Первый член ряда для преобразованной функции (2.5)
H1(p) = I(1 – e–pt)/(E – RI)p.
Таким образом, первый член h(t) ряда для переходной проводимости будет представлять согласно (2.1) импульс прямоугольной формы длительностью t, начинающийся в момент времени t = 0, с амплитудой I/(E – RI) (рис. 2.3). Второй член имеет преобразованную функцию
H2(p) = –H1(p)e–pt/(E/RI – 1).
Согласно теореме запаздывания умножение преобразованной функции на e–ptсоответствует смещению исходной функции в сторону положительных значений t на величину t. Следовательно, вторая составляющая исходной функции h2(t) так же, как и первая, представляет собой импульс прямоугольной формы, отличающийся знаком и амплитудой и начинающийся в момент времени t = t. Продолжая почленные преобразования, придем к последовательности прямоугольных импульсов в виде, представленном на рис. 2.3 для случая (E/RI – 1)>1.
При (E/RI – 1) < 1 амплитуды импульсов со временем нарастают, что физически неосуществимо на практике. Первый случай соответствует требованию, чтобы амплитуда импульса напряжения на нагрузке U = RI была меньше E/2, второй – больше E/2. При (E/RI – 1) = 1, т. е. при заданной амплитуде импульса тока I = E/2R, или, что то же самое, при заданной амплитуде импульса напряжения на сопротивлении нагрузки U = RI = E/2 амплитуды импульсов будут неизменными.
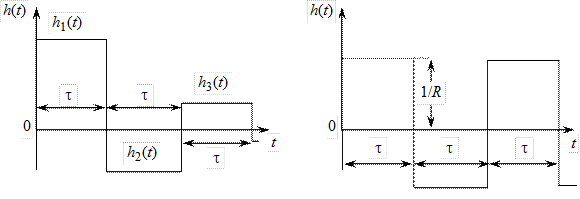
Рис. 2.3 Рис. 2.4
На рис. 2.4 представлена переходная проводимость ФД для случая E/RI – 1 = 1, что и представляет собой практический интерес. Операционное сопротивление этого двухполюсника, как следует из формулы (2.3),
Z(p) = R(1 + e–pt)/(1 – e–pt). (2.6)
Аналогично может быть найдена переходная функция для ФД при наличии источника перепада тока (единичной ступенчатой функции тока). В этом случае схема (рис. 2.5) представляет собой параллельное соединение нагрузки R, источника перепада тока i(t) и ФД. В качестве переходной функции выберем переходное сопротивление 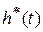 , т. е. зависимость от времени напряжения на ФД при воздействии на него единичного перепада тока i0(t)=1(t) (рис. 2.6).
, т. е. зависимость от времени напряжения на ФД при воздействии на него единичного перепада тока i0(t)=1(t) (рис. 2.6).
Преобразованная функция 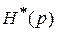 для переходного сопротивления определяется из следующего операционного уравнения:
для переходного сопротивления определяется из следующего операционного уравнения:
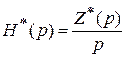 , (2.7)
, (2.7)
где 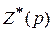 – операционное сопротивление ФД.
– операционное сопротивление ФД.
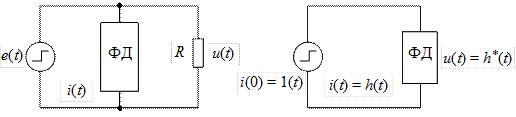
Рис. 2.5 Рис. 2.6
Операционное уравнение для схемы формирования (рис. 2.5) может быть записано в следующем виде:
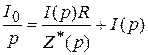 ,
,
где 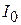 – величина перепада тока
– величина перепада тока 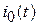 . Отсюда
. Отсюда
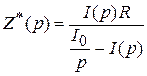 . (2.8)
. (2.8)
Подставив зависимость (2.8) в (2.7), получим с учетом (2.1) следующее уравнение для преобразованной переходной функции:
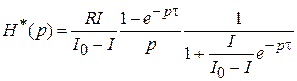 . (2.9)
. (2.9)
После разложения последней дроби в выражении (2.9) в бесконечный ряд получим
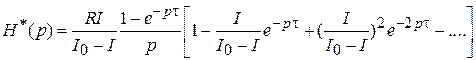 .
.
При 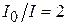 обратное преобразование дает переходное сопротивление
обратное преобразование дает переходное сопротивление 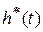 в виде периодической ступенчатой функции, аналогичной переходной функции, представленной на рис. 2.4.
в виде периодической ступенчатой функции, аналогичной переходной функции, представленной на рис. 2.4.
