Канонические уравнения кривых II порядка
При некотором специальном выборе осей координат уравнение (1) имеет более простые формы.
1. Эллипс. Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
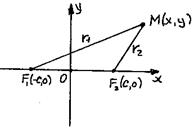 Т.к. точки F1, F2 заданы, то известно расстояние |F1F2| = 2c (фокусное расстояние). Для вывода уравнения эллипса выберем ось ОХ проходящей через фокусы, а начало координат – посередине отрезка F1F2.
Т.к. точки F1, F2 заданы, то известно расстояние |F1F2| = 2c (фокусное расстояние). Для вывода уравнения эллипса выберем ось ОХ проходящей через фокусы, а начало координат – посередине отрезка F1F2.
r1 = |MF1| и r2 = |MF2| - фокальные радиусы точки М. По определению: r1 + r2 = 2a (2a > 2c). Но 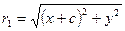 и
и 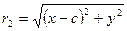 . Значит:
. Значит: 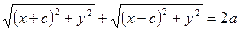 . Это и есть уравнение эллипса. Упростим его:
. Это и есть уравнение эллипса. Упростим его:
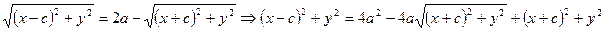
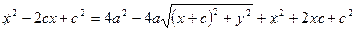
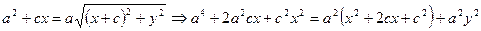
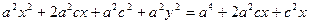 ,
, 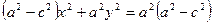
Разделим на а2 – с2: 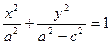 . Из
. Из 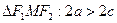 , т.е. а > c и значит, а2 – с2 > 0, поэтому обозначим а2 – с2 = b2. Окончательно:
, т.е. а > c и значит, а2 – с2 > 0, поэтому обозначим а2 – с2 = b2. Окончательно:
 (1)
(1)
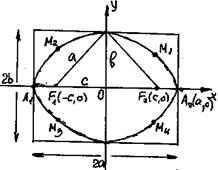 Это уравнение эллипса называется каноническим. Исследуем форму кривой по ее каноническому уравнению.
Это уравнение эллипса называется каноническим. Исследуем форму кривой по ее каноническому уравнению.
1. Из (1) следует, что эллипс – ограниченная кривая: 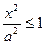 ;
; 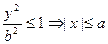 ;
; 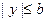 , т.е. все точки кривой содержатся в прямоугольнике с основанием 2а и высотой 2b.
, т.е. все точки кривой содержатся в прямоугольнике с основанием 2а и высотой 2b.
2. Если точка М1(х1, у1) 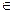 k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1)
k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1) 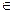 k, т.к. переменные х и у входят в (1) только в квадратах. Т.о., эллипс имеет две оси симметрии – ось ОХ и ось OY и центр симметрии – начало координат.
k, т.к. переменные х и у входят в (1) только в квадратах. Т.о., эллипс имеет две оси симметрии – ось ОХ и ось OY и центр симметрии – начало координат.
3. Найдем точки пересечения с осями координат:
х = 0 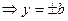 ; у = 0
; у = 0 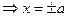 . Если a > b, то
. Если a > b, то
|A1A2| = 2a – большая ось эллипса; |OA2| = a – большая полуось.
|B1B2| = 2b – малая ось эллипса; |OB2| = b – малая полуось.
4. Точки A1, A2, B1, B2 – вершины эллипса.
5. Для точек I четверти из (1): 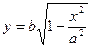 . Когда х возрастает от 0 до а, то у уменьшается от b до 0.
. Когда х возрастает от 0 до а, то у уменьшается от b до 0.
 Замечание: В частном случае, если b = a = R, то (1) превращается в уравнение окружности: x2 + y2 = R2.
Замечание: В частном случае, если b = a = R, то (1) превращается в уравнение окружности: x2 + y2 = R2.
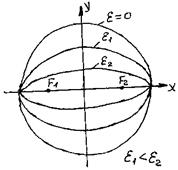
Отношение фокусного расстояния |F1F2| к длине большой оси |A1A2| называется эксцентриситетом. Эксцентриситет характеризует форму эллипса. 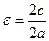 ,
, 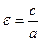 , т.к. с< а, то
, т.к. с< а, то 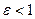 . Фиксируем большую ось а эллипса и будем изменять
. Фиксируем большую ось а эллипса и будем изменять 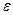 . Т.к. b2 = a2 – c2, то
. Т.к. b2 = a2 – c2, то 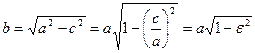 , а
, а 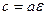 .
.
Если 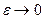 , то с уменьшается:
, то с уменьшается: 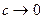 , т.е. фокусы сближаются. При этом
, т.е. фокусы сближаются. При этом 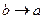 и эллипс в пределе превращается в окружность.
и эллипс в пределе превращается в окружность.
Если 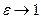 , то
, то 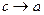 и
и 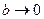 , т.е. эллипс превращается в отрезок прямой.
, т.е. эллипс превращается в отрезок прямой.
2. Гипербола. Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
Выберем систему координат так же, как и при выводе уравнения эллипса: ось ОХ проходит через фокусы F1 и F2, а точка О делит расстояние между фокусами пополам:
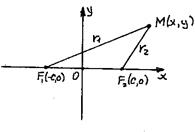 Обозначим: |F1F2| = 2c, тогда F1(c, 0); F2(-c, 0). Возьмем произвольную точку на гиперболе M(x, y). Тогда
Обозначим: |F1F2| = 2c, тогда F1(c, 0); F2(-c, 0). Возьмем произвольную точку на гиперболе M(x, y). Тогда 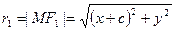 ;
; 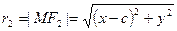 . По определению гиперболы: r2 – r1 = ±2a. Знак «+», если r2 > r1, а знак «-», если r2 < r1. Или
. По определению гиперболы: r2 – r1 = ±2a. Знак «+», если r2 > r1, а знак «-», если r2 < r1. Или 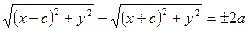
Это и есть уравнение гиперболы. Упростим его, избавившись от радикалов:
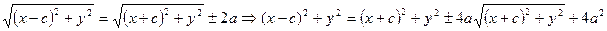 ,
, 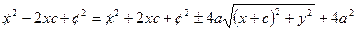 ,
, 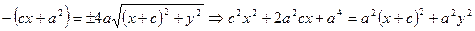 ,
, 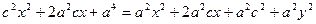 ,
, 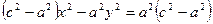 .
.
Разделим на а2(с2 – а2): 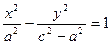 . Из
. Из 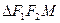 : |F1F2| = 2c, а r1 – r2 =2a. По свойствам сторон треугольника: 2c > 2a; c > a: c2 – a2 > 0. Поэтому обозначим с2 – а2 = b2. Теперь уравнение гиперболы принимает канонический вид:
: |F1F2| = 2c, а r1 – r2 =2a. По свойствам сторон треугольника: 2c > 2a; c > a: c2 – a2 > 0. Поэтому обозначим с2 – а2 = b2. Теперь уравнение гиперболы принимает канонический вид:
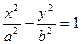 (2)
(2)
Исследуем это уравнение.
1. В отличие от эллипса, гипербола – неограниченная кривая: 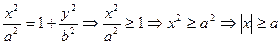 . Все точки гиперболы лежат вне вертикальной полосы шириной 2а , а между прямыми х = -а и х = а кривая точек не имеет.
. Все точки гиперболы лежат вне вертикальной полосы шириной 2а , а между прямыми х = -а и х = а кривая точек не имеет.
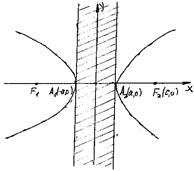 2. Если М1(х1, у1)
2. Если М1(х1, у1) 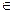 k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1)
k, то и точки М2(-х1, у1); М3(-х1, -у1); М4(х1, -у1) 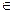 k, т.к. координаты х и у входят в уравнение (2) только в четных степенях. Поэтому, как и эллипс, гипербола имеет две оси симметрии – OX и OY и центр симметрии – начало координат.
k, т.к. координаты х и у входят в уравнение (2) только в четных степенях. Поэтому, как и эллипс, гипербола имеет две оси симметрии – OX и OY и центр симметрии – начало координат.
3. Точки пересечения с осями координат:
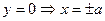 , А1(-а, 0), А2(а, 0);
, А1(-а, 0), А2(а, 0);
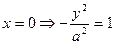 - кривая ось OY не пересекает (мнимая ось).
- кривая ось OY не пересекает (мнимая ось).
4. |A1A2| = 2a – действительная ось гиперболы; |OA2| = a – полуось;
|B1B2| = 2b – мнимая область; |OB2| = b – мнимая полуось.
5. Точки пересечения главных осей с гиперболой называются вершинами гиперболы. Гипербола имеет две вершины: А1(-а, 0) и А2(а, 0).
6. Для точек I четверти: 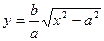 (
( 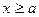 ). Если х изменяется от а до
). Если х изменяется от а до 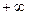 , то у изменяется от 0 до
, то у изменяется от 0 до 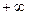 и точка уходит по кривой в бесконечность.
и точка уходит по кривой в бесконечность.
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси: 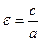 . Для гиперболы
. Для гиперболы 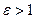 .
.
Асимптоты гиперболы.
Рассмотрим подробнее, как именно точка М по кривой уходит в бесконечность. Из (2): 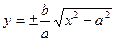 . Если х неограниченно возрастает, то подкоренное выражение мало отличается от х2 и кривая почти не отличается от прямой
. Если х неограниченно возрастает, то подкоренное выражение мало отличается от х2 и кривая почти не отличается от прямой 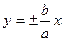 .
.
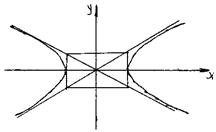 Т.о., при удалении точки М по кривой в бесконечность, она неограниченно приближается к одной из двух прямых:
Т.о., при удалении точки М по кривой в бесконечность, она неограниченно приближается к одной из двух прямых: 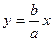 или
или 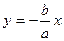 . Эти прямые называются асимптотами гиперболы.
. Эти прямые называются асимптотами гиперболы.
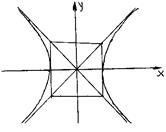 Если a = b, то основным прямоугольником гиперболы будет квадрат и получаем равнобочную гиперболу: х2 – у2 = а2.
Если a = b, то основным прямоугольником гиперболы будет квадрат и получаем равнобочную гиперболу: х2 – у2 = а2.
Пример. Гипербола проходит через точку М1(1, 2), е = 3. Найти асимптоты.
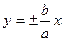 ;
; 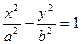 ;
; 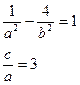 ;
; 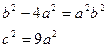 ;
;
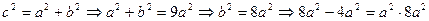 ;
;
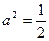 ;
; 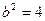 ;
; 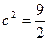 ;
; 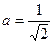 ; b = 2;
; b = 2; 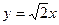 ;
; 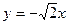 .
.
