Сформулировать определение ортонормированного базиса

12)

Cos(a)=	|A1·A2 + B1·B2 + C1·C2|
(A12 + B12 + C12)1/2(A22 + B22 + C22)1/2

49) Условие принадлежности прямой плоскости

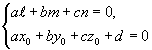
Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными.

Так, например, на рис. 20 векторы BC^> и AD^> коллинеарны, а векторы AB^> и AC^> неколлинеарны.

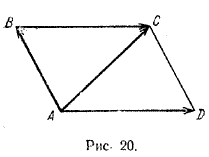
Если векторы а и b коллинеарны, то говорят также, что вектор а коллинеарен векторуb, а вектор b коллинеарен вектору а.

Нулевой вектор считается коллинеарным любому вектору.

Теорема (признак коллинеарности). Для того чтобы вектор а был коллинеарен ненулевому вектору b, необходимо и достаточно, чтобы существовало число k, удовлетворяющее условию

a = kb. (1)

Достаточность. Если при некотором k равенство (1) выполняется, то векторы b и аколлинеарны по определению умножения вектора на число и определению коллинеарных векторов.

Необходимость. Пусть вектор а коллинеарен ненулевому вектору b. Возможны следующие три случая: а 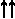b, а b, а = 0.

Если а 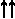b, то a = 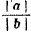• b, т. е. равенство (1) выполняется при k =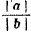

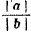Если а b , то a = — • b, т. е. равенство (1) выполняется при k = —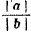

Если а = 0, то а = 0 • b , т. е. равенство (1) выполняется при k= 0.

Задача. Доказать, что векторы AВ^> + СВ^> + 2 ВА^> и ¹/₃ AС^> коллинеарны.

Используя свойства операций над векторами, получим

AВ^> + СВ^> + 2 ВА^> = (AВ^> + ВА^>) + (СВ^> + ВА^>) = 0 + ВА^> = ВА^> = — АС^>.

Таким образом,

AВ^> + СВ^> + 2 ВА^> = —3 (¹/₃ AС^>) .

По признаку коллинеарности векторов данные в условии векторы коллинеарны.

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

A₁x + B₁y + C₁ = 0,

A₂x + B₂y + C₂ = 0, (6)

угол между ними определяется по формуле

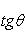
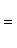
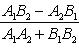
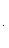(7)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

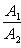
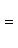
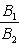
(9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

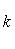
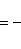
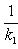
(10)

Это условие может быть записано также в виде

k₁k₂ = -1. (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0. (12)

Колычков!

Миронова

Аналитическая геометрия.

14 вопрос: дать определение равенства двух свободных векторов.

Два вектора равны тогда и только тогда, когда они коллинеарны, сонаправленны, имеют равные длины.

Вопрос 33: записать формулы для вычисления координат точки, делящей отрезок в заданном отношении.

М(x,y,z) - точка; |АМ|/|MB|=λ/μ ; А(x1,y1,z1) ; B(x2,y2,z2); λ; μ > 0; λ+μ ≠ 0

формулы в координатах: x=( μх1+ λх2)/( λ+ μ)

y=( μy1+ λy2)/( λ+ μ)

z=( μz1+ λz2)/( λ+ μ)

Вопрос 52: сформулировать условия параллельности и перпендикулярности двух плоскостей. сформулировать определение скалярного произведения. вывести формулу для вычисления скалярного произведения двух векторов, заданных в ОНБ. сформулировать свойства скалярного произведения.

параллельность 2-х плоскостей: если 2 пересекающиеся прямые одной плоскости соответственно параллельны 2м пересекающимся прямым другой плоскости, то такие плоскости параллельны.

перпендикулярность 2 -х плоскостей: если одна плоскость содержит в себе перпендикуляр к другой плоскости, то такие плоскости перпендикулярны.

скалярное произведение: скалярным произведением 2х векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Пусть ОНБ: i,j,k.

a=α1i+ α2j+ α3k;

b=β1i+ β2j+ β3k;

(a, b)=( α1i+ α2j+ α3k)*( β1i+ β2j+ β3k)= α1β1+ α2 β2+ α3 β3;

свойства скалярного произведения:

1. скалярное произведение коммутативно

(a,b)=(b,a)

2. для любого a скалярное произведение вектора самого на себя есть квадрат длины этого вектора. (a,a)=|a|²

3. скалярное произведение равно 0 тогда и только тогда, когда сомножители ортогональны или хотя бы 1 из них равен нулевому вектору.

4. векторы ортонормированного базиса удовлетворяют следующим соотношениям:

(i, i)=(j, j)=(k, k)=1;

(i, j)=(j, k)=(k, i)=0.

Миронова

Белинский

4) Дать определение геометрического вектора и орта вектора.

Геометрический вектор – направленный отрезок или упорядоченная пара точек.

Орт вектора (единичный вектор) – вектор, длина которого равна единице.

23) Записать формулу для вычисления ортагональной проекции вектора на заданное направление.

пр_Īā=IāIcos(a,^˄ l)

42)Сформулировать определение коллинеарности двух векторов и доказать теорему о необходимом и достаточном условии коллинеарности двух векторов.

Два вектора коллинеарны, если они расположены на одной прямой или на параллельных прямых.

Необходимым и достаточным условием коллинеарности ненулевого вектора ā и вектора b является существование такого числа x, которое удовлетворяет равенству ā=λb .

Дано: ā=x1i+y1j+z1k; b=x2i+y2j+z2k.

Доказать: ā=λb.

Доказательство:

Пусть вектор ā коллинеарен вектору b. Тогда x1/x2=y1/y2=z1/z2. Обозначим коэффициент пропорциональности через λ. Тогда x1=λx2, y1=λy2,z1=λz2. Следовательно ā=x1i+y1j+z1k= λx2i+λy2j+λz2k=λ(x2i+y2j+z2k)= λb.

Ч.т.д.

Белинский

Новопокровский

№15 Смешанным произведением некомпланарных векторов a, b, c , взятых в данном порядке, называется скалярное произведение вектора а на векторное произведение b и c

Выведение формулы: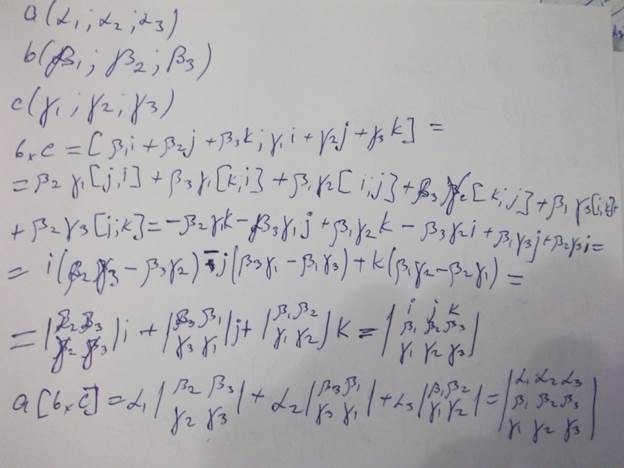

Свойства:

1)Смешанное произведение кососимметрично по отношению ко всем своим аргументам(меняет знак на противоположный при перемене мест 2-х сомножителей)

2)Смешанное произведение в правом прямоугольном базисе равно определителю матрицы(см выше формулу). В левом – определителю, взятом с минусом.

3)Модуль смешанного произведения равен объему параллелепипеда, взятому на этих векторах.

4) Смешанное произведение линейно по каждому аргументу.

Линейность операции по какому-то аргументу означает выполнение двух условий:

а) если аргумент умножить на число, то и результат умножится на это число, то есть числовой множитель аргумента можно вынести за знак операции;

б) если аргумент заменить суммой двух слагаемых, то результат будет равен сумме результатов для каждого слагаемого.

5) Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.

6)Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

№34 Общее уравнение прямой в пространстве(через координаты плоскостей):

A₁x+B₁y+C₁z+D₁=0

A₂x+B₂y+C₂z+D₂=0

Где x,y,z – координаты точки М, принадлежащей прямой

Векторное уравнение прямой в пространстве:

rˉ=tsˉ+r₀ˉ

Где rˉ- радиус вектор от центра координат до точки М, принадлежащей прямой.

r₀ˉ - радиус вектор от начала координат до точки М₀

sˉ-направляющий вектор к данной прямой.

Поскольку sˉ коллиниарен ММ₀ˉ, то ММ₀ˉ=tsˉ, где т – параметр, равный отношению соответствующих координат векторов.

Параметрическое уравнение прямой в пространстве:

Запишем векторное уравнение в координатной форме.

, , =>

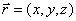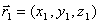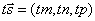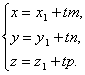
Канонические уравнения прямой

Пусть М1(x1, y1, z1) – точка, лежащая на прямой l, и 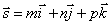– её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор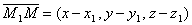

Векторы 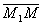и 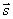коллиниарны, следовательно, их соответствующие координаты пропорциональны. Получаем канонические уравнения:

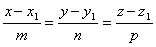
Новопокровский

Гришин

5) дать опеределение коллинеарности и компланарности вектров.

Два ненулевых вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой.

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.

24) записать формулу для вычисления расстояния между 2мя скрещивающимися прямыми. Сформулировать определения скалярного произведения. Вывести формулу для вычисления скалярного произведения 2х векторов, заданных в ортонормированном базисе. Сформулировать свойства скалярного произведения.

А)Пусть прямые заданы векторными параметрическими уравнениями:

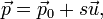
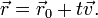
Тогда расстояние между ними можно определить, используя операции смешанное произведение и векторное произведение:

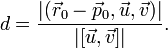(наверху модуль смешанного, внизу модуль векторного)

Б)скалярным произведением 2х векторов называется произведение длин этих вектров на косинус угла между этими векторами.

В) ab = (xai + yaj + zak)(xbi + ybj + zbk) =

= xaxbii + xaybij + xazbik + yaxbji + yaybjj + yazbjk + zaxbki + zaybkj + zazbkk =

= xaxbi2 + yaybj2 + zazbk2 = xaxb + yayb + zazb

Г)коммутативность ab = ba:

Ассоциативность (Oa)b = O(ab):

Дистрибутивность (a + b)c = ac + bс

Свойство скалярного квдарата: а^2>=0 ,причем а^2=0 только тогда,когда а=0

сформулировать определение ортонормированного базиса.

Тройка векторов 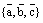называется ортонормированной, если она ортогональная и длины всех векторов равны единице: .

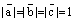Гришин

Ларичев

Вопрос 13-Дать определение ортонормированному базису. Сформулировать теорему о разложении вектора по базису.

Ортонормированный или ортогональный базис есть базис, составленный из попарно ортогональных (взаимоперпендикулярных) векторов, называемыми базисными векторами.

Теорема. (О разложении вектора по базису.)

Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.

Доказательство. Пусть L произвольная прямая (или ось) и 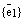–базис 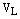. Возьмем произвольный вектор 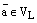. Так как оба вектора 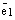и 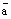коллинеарные одной и той же прямой L, то 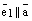. Воспользуемся теоремой о коллинеарности двух векторов. Так как 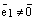, то найдется (существует) такое числ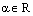о , что 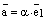и тем самым мы получили разложение вектора 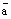по базису 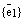векторного пространства .

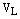Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора 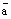по базису 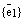векторного пространства :

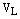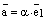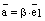и , где 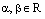. Тогда 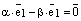и используя закон дистрибутивности, получаем:

.

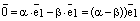Так как 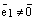, то из последнего равенства следует, что 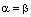, ч.т.д.

Вопрос 32. Записать формулы для вычисления длины вектора, заданного своими координатами в ортонормированном базисе и косинуса угла между векторами.

|a|=корень из (x^2+y^2+z^2) (Длина вектора равна квадратному корню из суммы квадратов его координат)

Cos A = (a*b)/(|a|*|b|)(косинус угла между векторами равен отношению скалярного произведения векторов на произведение длин векторов).

Вопрос 51. Сформулировать условия параллельности и перпендикулярности двух плоскостей. Перечислить основные виды уравнений плоскости в пространстве. Указать геометрический смысл входящих в них параметров.

Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

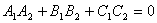Плоскости параллельны, векторы нормалей коллинеарны: 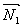ïï 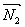.Это условие выполняется, если: .

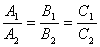Ax + By + Cz +D = 0

x/a+y/b+z/c=1

x*cos A+y*cos B+z*cos C-p=0

A(x-x0)+B(y-y0)+C(z-z0)=0

A,B,C-константы,A^2+B^2+C^2 неравно нулю(три константы неравны нулю одновременно)

Ларичев С (13)

Корякин

Вопрос 12

Элементарное описание ортогональной проекции точки на прямую сводится к тому, что из точки на прямую следует опустить перпендикуляр, и его пересечение с прямой даст образ точки (проекцию точки на эту прямую). Это определение работает и на плоскости, и в трехмерном пространстве, и в пространстве любой размерности.

Элементарное определение проекции вектора на прямую легче всего дать, представив вектор направленным отрезком. Тогда на прямую можно спроектировать его начало и его конец, и направленный отрезок от проекции начала к проекции конца исходного вектора даст его проекцию на прямую.

Проекцией вектора на некоторое направление обычно называют число, совпадающее по абсолютной величине с длиной проекции этого вектора на прямую, определяющую это направление; знак же числа выбирается так, что оно считается положительным, когда направление этой проекции совпадает с данным направлением, и отрицательным, когда направление противоположно.