Расчет на прочность цилиндрических передач

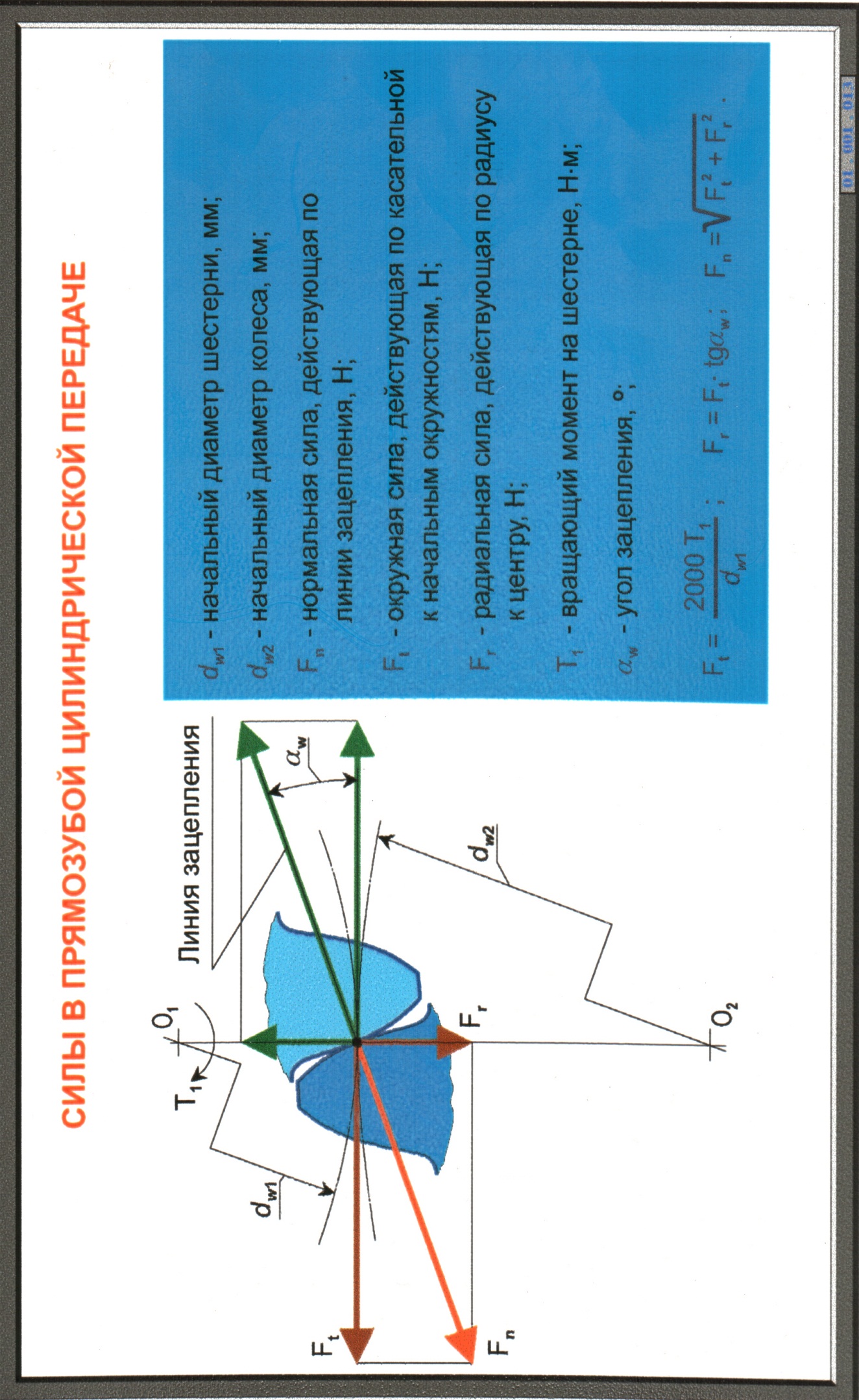
Контакт зубьев рассматривают в полюсе зацепленияР как контакт двух цилиндров с радиусами ρ1 и ρ2, равными радиусами кривизны эвольвенты в полюсе зацепления.

Наибольшее контактное напряжение в зоне зацепления при линейном контакте определяют по формуле Герца. Для стальных колес с коэффициентом Пуассона µ =0.3 имеет вид:

σн = 0.418√qЕпр/Рпр
q – нормальная нагрузка на единицу длины контактных линий.

Епр – приведенный модуль упругости материала колес

Рпр – приведенный радиус кривизны зубьев

Вводя в эту формулу коэффициенты, учитывающие:

- геометрические передачи;

- свойства материала колес;

- неравномерность и динамичность нагрузки;

получают формулу для определения главного параметра зубчатой передачи – межосевого расстояния аw.

аw = Ка(U+1)³√KнТ1/ψbaU[σ]²н

Кн– коэффициент нагрузки (учитывает условия нагружения)

Т1 – вращающий момент на шестерне, Н·м

[σ]н – допуск контактных напряжений, Н/мм²

ψbа – коэффициент ширины венца колеса

Ка– коэффициент межосевого расстояния, (Н/мм²)⅓

Эту формулу используют для проектировочного расчета закрытых цилиндрических передач со стальными колесами.

После уточнения межосевого расстояния по ГОСТ выполняют проверочный расчет передачи:

σн = Zσ/aw√KнT1(U+1)³/b2U≤[σ]н,

где Zσ – коэффициент различный для косозубых и прямозубых передач;

b2 – ширина зубчатого венца колеса, мм

Величину [σ]н определяют по пределу контактной выносливости [σ]нlim с учетом влияния на контактную прочность:

- ресурса передачи;

- шероховатости поверхности зубьев;

- быстроходности передачи;

- запаса прочности.

Контактная прочность зубьев зависит от материала колес и габаритных размеров передачи и не зависит от модуля или числа зубьев в отдельности!!!!

Для обеспечения контактной прочности при определенном межосевом расстоянии модуль и число зубьев могут иметь различные значения с соблюдением условия:

m(Z1+Z2)/2 = aw

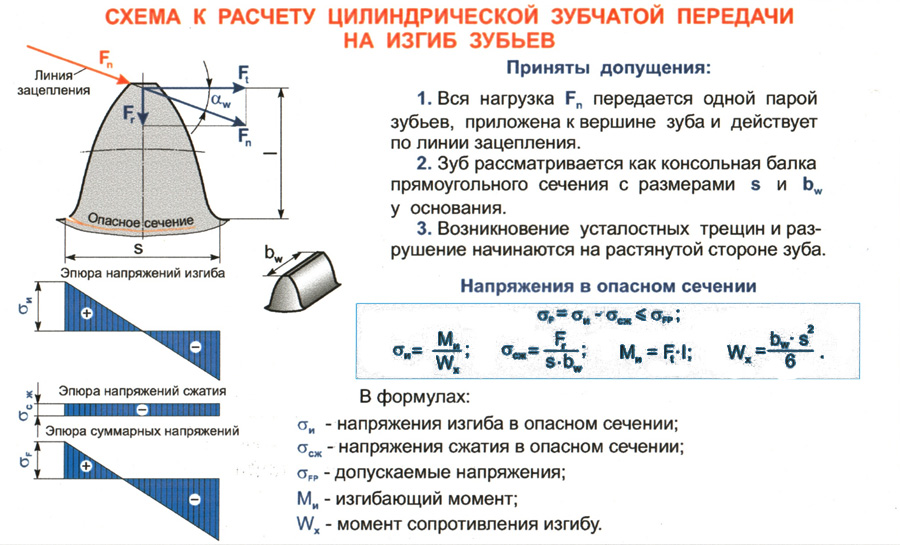
Расчет зубчатых передач на прочность при изгибе проводят как проверочный. Зуб рассматривают как консольную балку, нагруженную сосредоточенной силойFn, Fn = Ft/cosα. СилуFnпереносят по линии зацепления до оси зуба и полученную точку О принимают за вершину параболы, которая определяет контур балки ровного сопротивления изгибу. Точки А и В касания ветвей параболы и профиля зуба определяют положение опасного сечения. При определении нормального напряжения а опасном сечении используют формулы сопротивления материалов с учетом концентрации напряжений. вызванной особой формой зубьев.

Условия прочности по напряжениям изгиба:

σF =( KFFt/bm)YFS≤[σ]F

KF – коэффициент нагрузки

YFS – коэффициент, учитывающий форму зуба

[σ]F – допускаемые напряжения изгиба

Величину [σ]Fопределяют по пределу выносливости при изгибе [σ]Flimс учетом влияния на прочность:

- ресурса передачи;

- шероховатость поверхности впадин между зубьями;

- реверсивности передачи и запаса прочности.

РАСЧЕТ НА ПРОЧНОСТЬ КОНИЧЕСКИХ И ЧЕРВЯЧНЫХ
ПЕРЕДАЧ

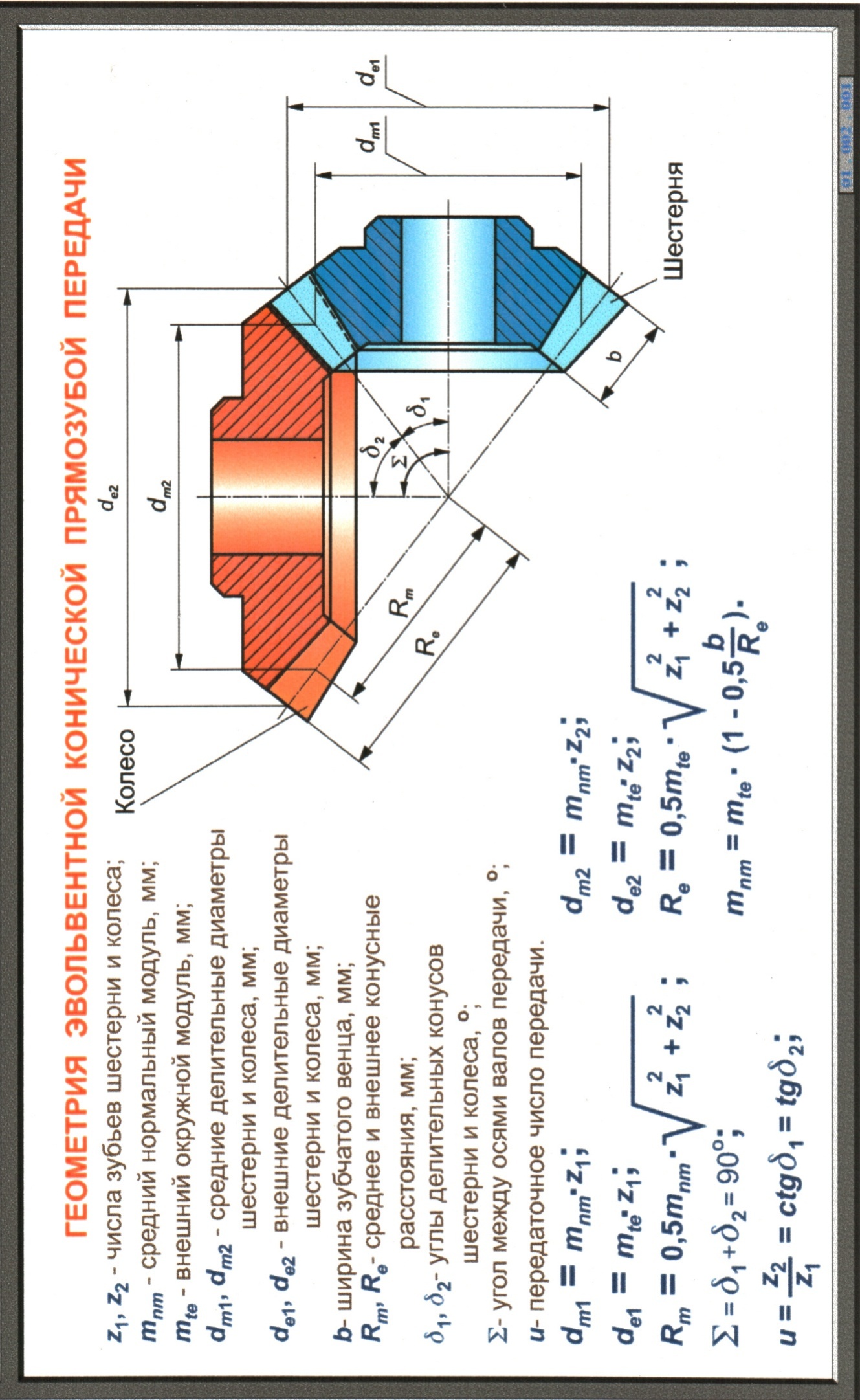
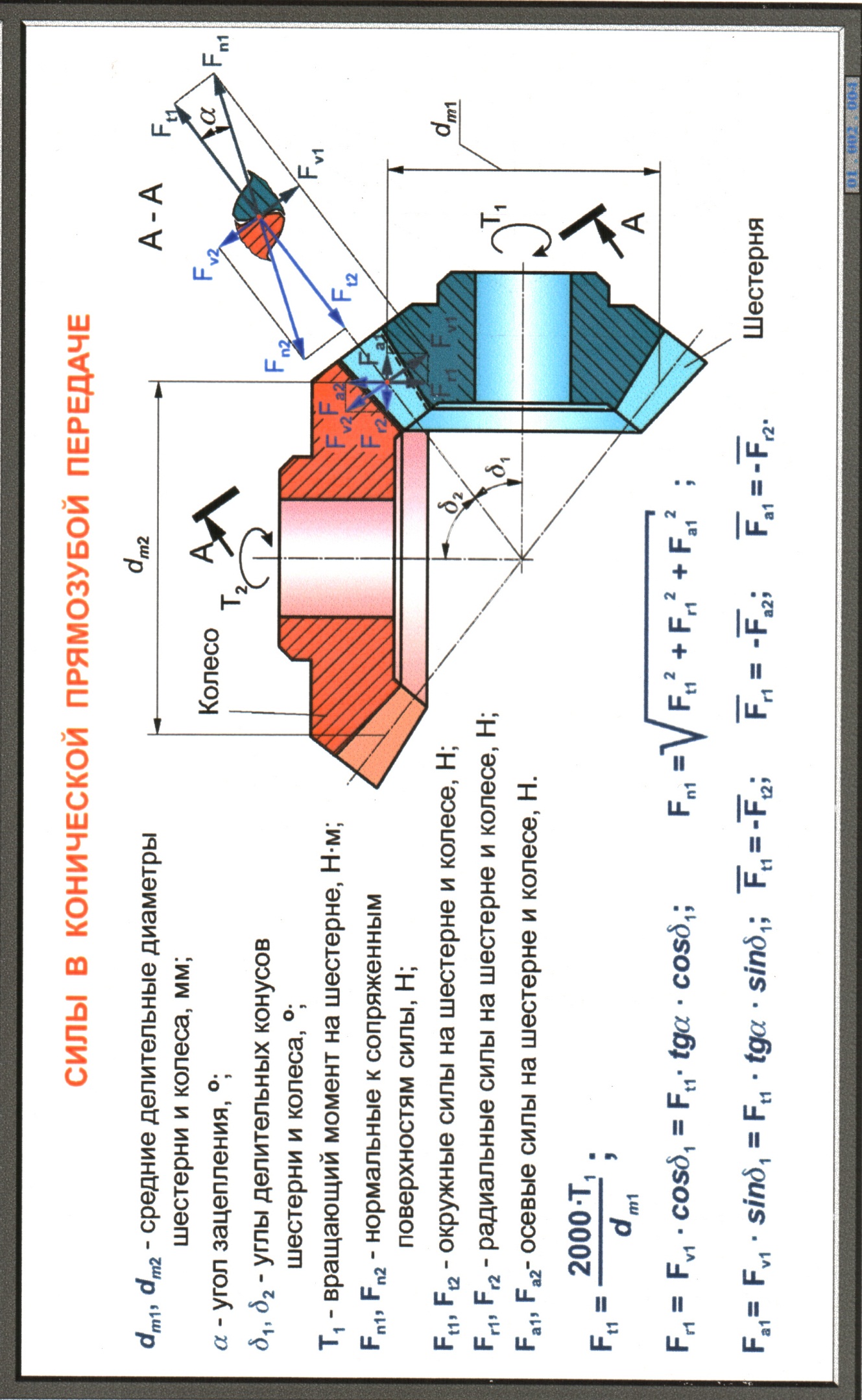
Исходные положения для расчета на прочность конических и червячных передач аналогичны применяемых при расчетах цилиндрических передач.Для червячной передачи дополнительно проводят тепловой расчет, т.к их работа сопровождается выделением большого количества теплоты. При недостаточном отводе тепла смазочные свойства масла ухудшаются, возникает опасность заедания и преждевременного выхода передачи из строя.

Раздел №4: Тепловой расчет червячной передачи

Тепловой расчет производят только для червячной передачи, т.к. из-за высоких скоростей скольжения в зацеплении выделяется большое количество тепла.Тепловой расчет производится на основе теплового баланса, т.е равенства тепловыделения Qви теплоотдачи Qо.

Тепловой поток червячной передачи в одну секунду, Вт:

Qв = 10³(1-η)Р,
где η – КПД червячной передачи

Р – мощность на червяке, кВт

Тепловой поток наружной поверхности корпуса редуктора в одну секунду, Вт (мощность теплоотдачи, Qо):

Qо = Кт·(tм-tв)·А·(1+λ),где

А – площадь поверхности корпуса, омываемая внутри маслом или его брызгами, а с наружи воздух, м²

λ – коэффициент, учитывающий отвод тепла днища редуктора в основании.

tм – температура масла в корпусе передачи, ºС

tв– температура воздуха вне корпуса, ºС

Кт– коэффициент теплопередачи

По условию теплового балансаQв = Qо

10³(1-η)Р1 = Кт(tм-tв)А(1+λ)

Отсюда температура масла в корпусе червячной передачи

tм = tв + 10³(1-η)Р1/ Кт А(1+λ) ≤ [t]м

При расчетах принимают [t]м = 95..110ºС

Если tм >[t]м,то увеличивают поверхность охлаждения (площадь А),предусмотрев оребрение корпуса (или применяют искусственное охлаждение).