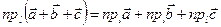Проекция вектора на ось
Лекции 3-5. Элементы векторной алгебры.
Величина, характеризуемая числом, называется скаляром. Примеры: длина отрезка, работа, масса, заряд температура и т.д.
Для характеристики других величин помимо числового значения необходимо указывать направление, а иногда и точку приложения. Примеры: сила, скорость, напряженность электрического поля и т.д. Это векторные величины.
В математике рассматривают так называемые геометрические векторы, для которых точка приложения не имеет значения (свободные векторы). Такой вектор можно перемещать в пространстве параллельно самому себе куда угодно.
Вектором называется направленный отрезок, проведенный из точки А в точку В. (Вектор – упорядоченная пара точек).
Обозначается: 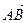 или
или 
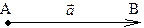
Точка А – начало вектора, точка В – конец вектора.
Длинной 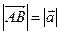 вектора
вектора 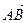 называется неотрицательное число, равное длине отрезка АВ. (Модуль).
называется неотрицательное число, равное длине отрезка АВ. (Модуль).
Если точки А и В совпадают, то имеем нулевой вектор: 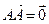 . Его модуль равен нулю, а направление не определено.
. Его модуль равен нулю, а направление не определено.
Два вектора  и
и 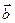 считаются равными, если они имеют равные модули, параллельны и одинаково направлены.
считаются равными, если они имеют равные модули, параллельны и одинаково направлены.

Два вектора называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.

Три вектора называются компланарными, если они параллельны одной плоскости.
Линейные операции над векторами.
1) Сложение векторов.
Сложение векторов производится по правилу параллелограмма или треугольника. Пусть  и
и 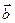 - два произвольных вектора.
- два произвольных вектора.
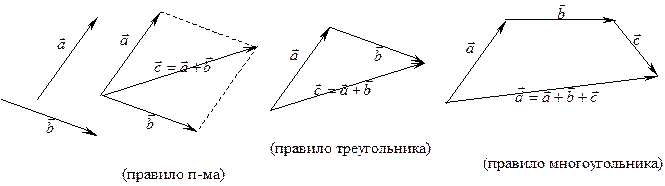
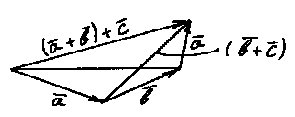 Операция сложения векторов подчиняется тем же законам, что и сложение чисел:
Операция сложения векторов подчиняется тем же законам, что и сложение чисел:
1. 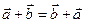 - переместительный закон (видно из параллелограмма);
- переместительный закон (видно из параллелограмма);
2. 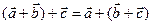 - сочетательный закон;
- сочетательный закон;
3. 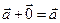 .
.
2) Вычитание векторов.
Под разностью двух векторов  и
и 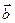 понимают вектор
понимают вектор 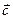 :
: 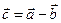 такой, что
такой, что 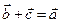 .
.
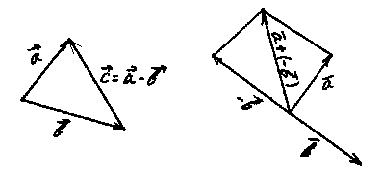 Для построения вектора
Для построения вектора 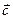 надо отложить вектора
надо отложить вектора  и
и 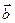 из общей точки. Затем надо соединить конец вектора – уменьшаемого с концом вектора вычитаемого и направить полученный вектор от вычитаемого к уменьшаемому.
из общей точки. Затем надо соединить конец вектора – уменьшаемого с концом вектора вычитаемого и направить полученный вектор от вычитаемого к уменьшаемому.
Вектор, коллинеарный данному вектору  , имеющий ту же длину, но противоположное направление, называется противоположным вектору
, имеющий ту же длину, но противоположное направление, называется противоположным вектору  и обозначается
и обозначается 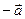 .
.
По правилу параллелограмма очевидно имеем: 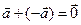 . Легко видеть, что
. Легко видеть, что 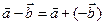 .
.
Умножение вектора на скаляр.
Пусть вектор  нужно умножить на действительное число л.
нужно умножить на действительное число л.
Произведением вектора  на скаляр л называется вектор
на скаляр л называется вектор 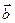 , модуль которого равен |л||
, модуль которого равен |л||  |, а направление совпадает с вектором
|, а направление совпадает с вектором  , если л>0 и меняется на противоположное, если л<0.
, если л>0 и меняется на противоположное, если л<0.
Умножение вектора на скаляр обладает следующими свойствами:
1. 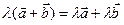 - распределительное свойство.
- распределительное свойство.
2. 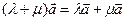 - распределительное свойство.
- распределительное свойство.
3. 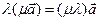 - сочетательное свойство.
- сочетательное свойство.
4. 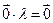 .
.
Единичный вектор.
Пусть имеется ненулевой вектор  (|
(|  |
| 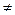 0).
0).

Разделим вектор  на его модуль, получим новый вектор:
на его модуль, получим новый вектор:
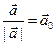
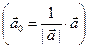 (*)
(*)
Модуль вектора 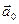 равен единице:
равен единице: 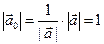 . Поэтому вектор
. Поэтому вектор 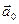 называется единичным вектором (ортом) того же направления, что и вектор
называется единичным вектором (ортом) того же направления, что и вектор  . Из (*) получается стандартная формула для вектора:
. Из (*) получается стандартная формула для вектора:
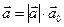
Замечание: Произведением вектора на число является вектор, коллинеарный исходному. Очевидно верно и обратное утверждение: любой вектор 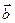 коллинеарный вектору
коллинеарный вектору  , может быть представлен в виде:
, может быть представлен в виде: 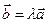 . Это – необходимое и достаточное условие коллинеарности.
. Это – необходимое и достаточное условие коллинеарности.
Проекция вектора на ось.
Если на прямой задано направление и указано начало, то прямая называется осью.
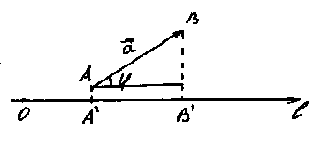 Из точек А и В опустим перпендикуляры на ось l. На оси l получим вектор
Из точек А и В опустим перпендикуляры на ось l. На оси l получим вектор 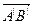 , который называется составляющей или компонентой вектора
, который называется составляющей или компонентой вектора 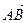 вдоль оси l.
вдоль оси l.
Проекцией вектора 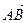 на ось l называется длина вектора
на ось l называется длина вектора 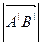 , взятая со знаком «+», если направления вектора
, взятая со знаком «+», если направления вектора 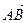 и оси l совпадают и со знаком «-» - в противном случае.
и оси l совпадают и со знаком «-» - в противном случае.
Из треугольника видно, что для вычисления проекции можно пользоваться формулой:
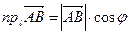
Если, 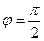 , то проекция равна нулю. В этой формуле знак проекции определяется знаком косинуса: если угол
, то проекция равна нулю. В этой формуле знак проекции определяется знаком косинуса: если угол 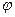 - острый, то проекция положительна, если тупой – отрицательна.
- острый, то проекция положительна, если тупой – отрицательна.
Свойства проекций.
1. При умножении вектора на скаляр его проекция также умножается на этот скаляр:
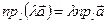
(Если гипотенуза изменится в л раз, то и катет изменится в л раз).
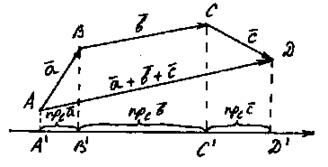 2. Проекция суммы векторов на любую ось равна алгебраической сумме слагаемых на ту же ось:
2. Проекция суммы векторов на любую ось равна алгебраической сумме слагаемых на ту же ось: