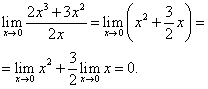Решение пределов через раскрытие неопределённостей

Основные теоремы о пределах

Теорема 1.(о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки 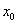, за исключением, может быть, самой точки 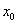, то либо они имеют один и тот же предел при 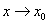, либо обе не имеют предела в этой точке.

Теорема 2.Если функции f(x) и g(x) имеют пределы в точке 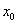, то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

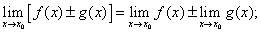(3)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

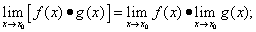(4)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

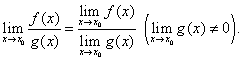(5)

Замечание.Формулы (3) и (4) справедливы для любого конечного числа функций.

Следствие 1.Предел постоянной равен самой постоянной, т.е.

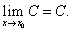
Следствие 2.Постоянный множитель можно выносить за знак предела, т.е.

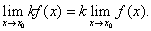
Пример 3.Найти предел:

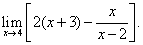
Решение.

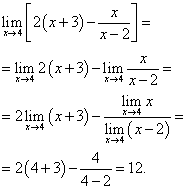
Пример 4.Найти предел:

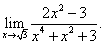
Решение. Предварительно убедимся, что предел делителя не равен нулю:

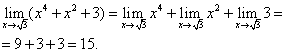
Таким образом, формула (5) применима и, значит,

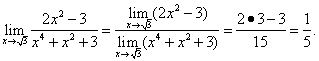
Теорема 3(о пределе сложной функции). Если существует конечный предел

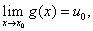
а функция f(u) непрерывна в точке 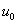, то

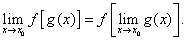
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.

Пример 5.Найти предел:

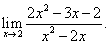
Решение. Теорема о пределе частного здесь неприменима, так как

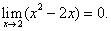
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим

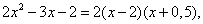
где

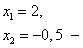
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:

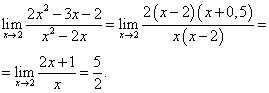
К началу страницы

Пройти тест по теме Предел

Решение пределов через раскрытие неопределённостей

При решении примера 5 нам уже встретилась неопределённость вида 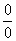. Эта неопределённость и неопределённость вида 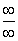- самые распространённые неопределённости, которые требуется раскрывать при решении пределов.

БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.

Освоим эти приёмы на примерах.

Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.

Неопределённость вида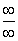

Пример 6.Раскрыть неопределённость 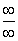и найти предел .

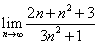Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :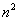

.

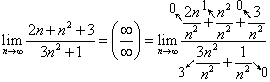Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или "супермалому числу".

Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .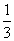

Пример 7.Раскрыть неопределённость 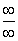и найти предел .

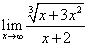Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:

.

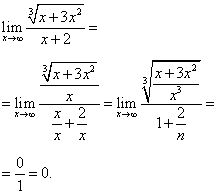Комментарий к ходу решения. В числителе загоняем "икс" под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо "икса".

Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.

Неопределённость вида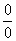

Пример 8.Раскрыть неопределённость 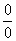и найти предел .

Решение. В числителе - разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:

.

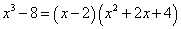В знаменателе - квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):

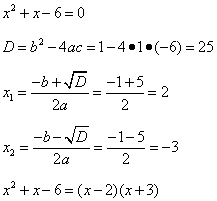
Запишем выражение, полученное в результате преобразований и найдём предел функции:

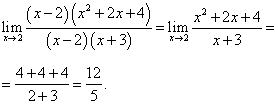
Пример 9. Раскрыть неопределённость 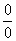и найти предел

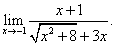
Решение. Теорема о пределе частного здесь неприменима, поскольку

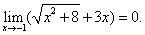
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:

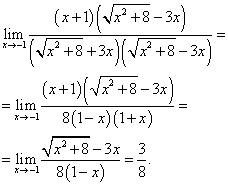
Пример 10. Раскрыть неопределённость 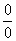и найти предел

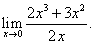
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел: