Векторное произведение векторов и его свойства
Определение. Векторным произведением векторов 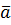 и
и 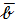 (обозначается
(обозначается 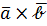 ) называется новый вектор , удовлетворяющий условиям:
) называется новый вектор , удовлетворяющий условиям:
1) 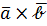 перпендикулярен обоим векторам, т.е. плоскости этих векторов:
перпендикулярен обоим векторам, т.е. плоскости этих векторов: 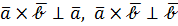 .
.
2) Направлен он так, что если смотреть с его конца, то поворот от первого вектора ко второму на наименьший угол видится происходящим против часовой стрелки.
3) 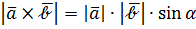 , т.е. длина векторного произведения равна произведению длин векторов на синус угла между ними. Иначе говоря, длина векторного произведения численно равна площади параллерограмма, построенного на векторах
, т.е. длина векторного произведения равна произведению длин векторов на синус угла между ними. Иначе говоря, длина векторного произведения численно равна площади параллерограмма, построенного на векторах 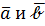 как на сторонах.
как на сторонах.
Вектор является математическим объектом, характеризуемым величиной (длиной) и направлением. В приведённом определении условия 1) и 2) определяют направление, а условие 3) – длину векторного произведения.
Из определения следуют свойства векторного произведения.
 Условие 2) определения означает, что
Условие 2) определения означает, что 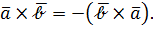 Это свойство названо антикоммутативностью.
Это свойство названо антикоммутативностью.
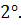 Для любого числа
Для любого числа 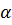 выполняется
выполняется 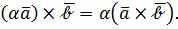
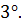
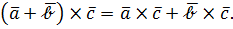
Первые три свойства позволяют оперировать с векторным произведением как с многочленами, не забывая только об антикоммутативности.
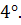 Из условия 3) следует, что
Из условия 3) следует, что 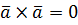 и, следовательно, равенство нулю векторного произведения есть условие коллинеарности векторов, т.е. получено ещё одно условие коллинеарности:
и, следовательно, равенство нулю векторного произведения есть условие коллинеарности векторов, т.е. получено ещё одно условие коллинеарности:
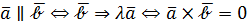 (14)
(14)
 (Векторное произведение в координатной форме). Пусть векторы заданы своими координатами:
(Векторное произведение в координатной форме). Пусть векторы заданы своими координатами:
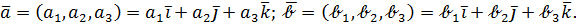
Как и в случае скалярного произведения, здесь также всё сводится к векторному произведению базисных векторов. Нетрудно убедится в справедливости следующей базисной таблицы векторного произведения.
 | 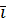 | 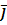 | 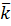 |
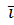 | 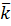 | 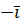 | |
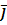 | 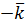 | 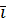 | |
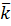 | 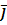 | 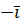 |
Руководствуясь этой таблицей, получим:
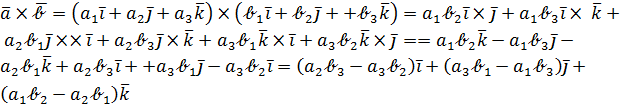 (15)
(15)
Эта формула громоздка для запоминания, зато легко запоминается формула
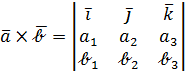 (16)
(16)
Легко убедиться в совпадении формул (15) и (16), надо лишь разложить определитель по первой строке.
Например, если 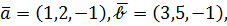 то
то 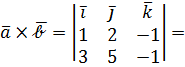
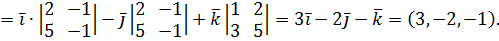
Переходя к примерам заметим, что в геометрии векторное произведение используется для нахождения площадей.
Пример 3. Дано: 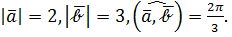
Найти 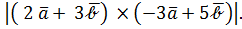
Решение. Отметим, что задача задана в бескоординатной форме, поэтому воспользуемся свойствами векторного произведения, позволяющими оперировать как с многочленами (не забывая об антикоммутативности 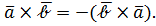
Раскроем сначала скобки под знаком модуля:
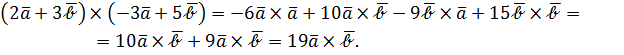
Мы учли, что 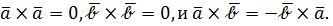
Теперь переходим к модулям: 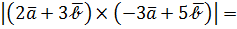
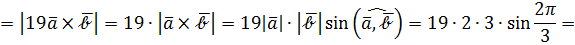
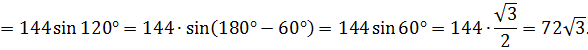
Пример 4. Дано: 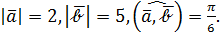 Вычислить площадь треугольника, построенного на векторах
Вычислить площадь треугольника, построенного на векторах 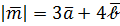 и
и 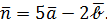
Решение. Вспоминаем пункт 3 определения векторного определения: 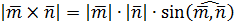 , т.е. модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.
, т.е. модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.
Следовательно, 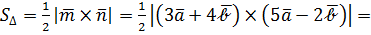
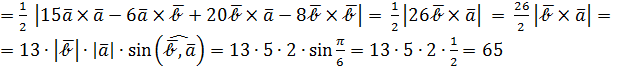 .
.
Ответ: 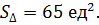
Пример 5. Найти вектор 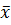 , который перпендикулярен векторам
, который перпендикулярен векторам 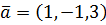 и
и 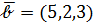 и удовлетворяет условию
и удовлетворяет условию 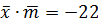 , где
, где 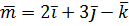 .
.
Решение. Можно, конечно, решать бесхитростно: ввести координаты вектора 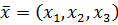 и для нахождения координат использовать три условия:
и для нахождения координат использовать три условия: 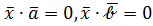 – условия перпендикулярности векторов
– условия перпендикулярности векторов 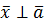 и
и 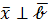 , а так же
, а так же 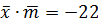 . В результате получим систему трёх уравнений с тремя неизвестными относительно
. В результате получим систему трёх уравнений с тремя неизвестными относительно 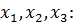
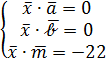
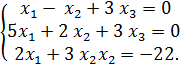
Решив эту систему, получим 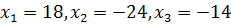 , т.е.
, т.е. 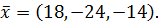
Изящнее и проще решать иначе. Обратим внимание на условие, что 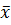 перпендикулярен векторам
перпендикулярен векторам 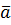 и
и 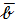 . Но ведь и векторное произведение
. Но ведь и векторное произведение 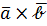 тоже вектор, который перпендикулярен векторам
тоже вектор, который перпендикулярен векторам 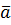 и
и 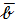 , следовательно, вектора
, следовательно, вектора 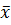 и
и 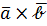 коллинеарны, т.е.
коллинеарны, т.е. 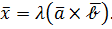 Найдём
Найдём 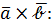
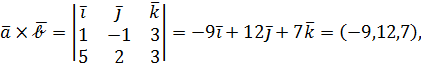
следовательно, 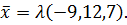 Тогда из условия
Тогда из условия 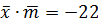 получим
получим 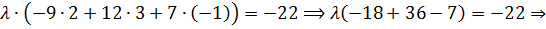
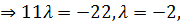 поэтому
поэтому 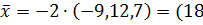 ,-24,-14).
,-24,-14).
Ответ: 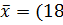 ,-24,-14).
,-24,-14).
