Линии на плоскости и их уравнения
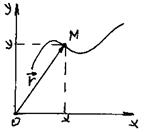 Линию на плоскости будем рассматривать как геометрическое место точек M(x, y), удовлетворяющих некоторому условию.
Линию на плоскости будем рассматривать как геометрическое место точек M(x, y), удовлетворяющих некоторому условию.
Если в декартовой системе координат записать свойство, которым обладают все точки линии, связав координаты и некоторые константы, можно получить уравнение вида: F(x, y) = 0 или 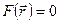 .
.
Пример. Написать уравнение окружности с центром в точке C(x0, y0) и радиуса R.
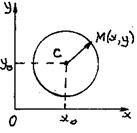 Окружность – геометрическое место точек, равноудаленных от точки С. Возьмем точку М с текущими координатами. Тогда |CM| = R или
Окружность – геометрическое место точек, равноудаленных от точки С. Возьмем точку М с текущими координатами. Тогда |CM| = R или 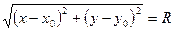 или
или 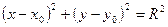 .
.
Если центр окружности находится в начале координат, то x2 + y2 = R2.
Не всякое уравнение вида F(x, y) = 0 определяет линию в указанном смысле: x2 + y2 = 0 – точка.
Прямая на плоскости.
Прямые на данной плоскости являются частным случаем прямых в пространстве. Поэтому их уравнения можно получить из соответствующих уравнений прямых в пространстве.
Общее уравнение прямой на плоскости. Уравнение прямой с угловым коэффициентом.
Любую прямую в плоскости XOY можно задать как линию пересечения плоскости Ax + By + Cz + D = 0 с плоскостью XOY: z = 0.
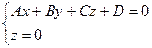 - прямая линия в плоскости XOY: Ax + By + D = 0.
- прямая линия в плоскости XOY: Ax + By + D = 0.
Полученное уравнение называется общим уравнением прямой. В дальнейшем его будем записывать в виде:
Ax + By + C = 0 (1)
1) Пусть 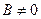 , тогда
, тогда 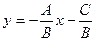 или y = kx + b (2) – уравнение прямой с угловым коэффициентом. выясним геометрический смысл k и b.
или y = kx + b (2) – уравнение прямой с угловым коэффициентом. выясним геометрический смысл k и b.
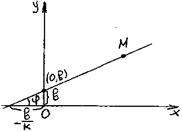 Положим x = 0. Тогда y = b – начальная ордината прямой.
Положим x = 0. Тогда y = b – начальная ордината прямой.
Положим y = 0. Тогда 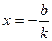 ;
; 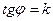 - угловой коэффициент прямой.
- угловой коэффициент прямой.
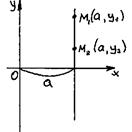 Частные случаи: а) b = 0, y=kx – прямая проходит через начало координат; б) k = 0, y = b – прямая параллельна оси ОХ; b) если B = 0, то Ax + C = 0,
Частные случаи: а) b = 0, y=kx – прямая проходит через начало координат; б) k = 0, y = b – прямая параллельна оси ОХ; b) если B = 0, то Ax + C = 0, 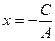 ,
,
x = a
Это - геометрическое место точек с постоянными абсциссами, равными a, т.е. прямая перпендикулярна оси ОХ.
Уравнение прямой в отрезках.
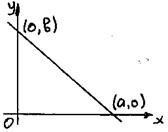 Пусть дано общее уравнение прямой: Ax + By + C = 0, причем
Пусть дано общее уравнение прямой: Ax + By + C = 0, причем 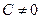 . Разделим обе его части на –C:
. Разделим обе его части на –C:
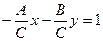 или
или 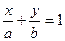 (3),
(3),
где 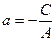 ;
; 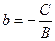 . Это уравнение прямой в отрезках. Числа a и b – величины отрезков, отсекаемых на осях координат.
. Это уравнение прямой в отрезках. Числа a и b – величины отрезков, отсекаемых на осях координат.
Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
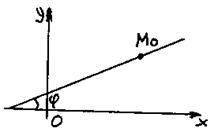 Пусть дана точка M0(x0, y0), лежащая на прямой L и угловой коэффициент k. Запишем уравнение:
Пусть дана точка M0(x0, y0), лежащая на прямой L и угловой коэффициент k. Запишем уравнение:
y = kx + b (*).
Здесь b неизвестно. Найдем его, учитывая, что M0 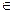 L:
L:
y0 = kx0 + b (**).
Вычтем почленно из (1) (2):
y – y0 = k(x – x0) (4).
Уравнение прямой, проходящей через данную точку в данном направлении.
Уравнение прямой, проходящие через две данные точки.
Пусть даны две точки M1(x1, y1) и M2(x2, y2) 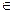 L. Запишем уравнение (4) в виде: y – y1 = k(x – x1). Т.к. M2
L. Запишем уравнение (4) в виде: y – y1 = k(x – x1). Т.к. M2 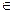 L, то y2 – y1 = k(x2 – x1). Поделим почленно:
L, то y2 – y1 = k(x2 – x1). Поделим почленно:
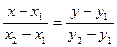 (5),
(5),
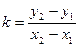 .
.
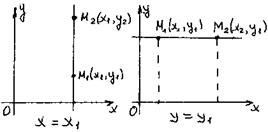 Это уравнение имеет смысл, если
Это уравнение имеет смысл, если 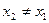 ,
, 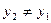 . Если x1 = x2, то M1(x1, y1) и M2(x1, y2). Если у2 = у1, то М1(х1, у1); М2(х2, у1).
. Если x1 = x2, то M1(x1, y1) и M2(x1, y2). Если у2 = у1, то М1(х1, у1); М2(х2, у1).
Т.о., если один из знаменателей в (5) обращается в нуль, надо приравнять нулю соответствующий числитель.
Пример. М1(3, 1) и М2(-1, 4). Написать уравнение прямой, проходящей через эти точки. Найти k.
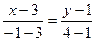 , 3х + 4у – 13 = 0,
, 3х + 4у – 13 = 0, 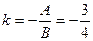 ;
; 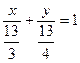 .
.
