Проверка 1974 г. КИ 1978 г. КИ Где учились на 1.03.81 г.

Алеша 15 лет 147 19 лет 155 4 к. физич. фак. МГПИ

Антон 13,5 лет 149 17,5 лет 160 4 к. хим.фак. МГУ

Оля 12 лет 132 16 лет 148 2 к. юр. фак. МГУ

Аня 10 лет 135 14 лет 156 3 к. мед. учил. № 3

Юля 7,5 лет 104 12 лет 146 2 к. библ. техникума

Ваня 5,5 лет – 9,5 лет 113 5 кл. Болш. школы №1

Люба 3 года – 7 лет 93 5 кл. Болш. школы №1

Отец 58 лет 110 62 года 120

Мать 44 года 122 48 лет 119

Тесты для взрослых выполнили не только 15-12-летние, но и 10-летняя Аня, и... чего я не ожидал – 7,5-летняя Юля. Таким образом, по тестам дети к 7-9 годам выходили на уровень среднего взрослого, а затем значительно превышали его (выше 130 баллов показывает только 1-3% взрослых).

Через 4 года, предполагая, что тесты достаточно хорошо забыты, я повторил проверку, причём для уверенности давал не по одному, а по два-три разных теста и учитывал средний результат нескольких измерений.

Родители оказались на уровне своих 9-10-летних детей, что, конечно, было немножко обидно, но с другой стороны, я стал относиться к детям с гораздо большим уважением, чем это обычно принято в семьях, и в выигрыше оказались как взрослые, так и дети.

Теперь оставалось сравнить наших детей с детьми, получившими обычное, традиционное развитие. Но тесты для взрослых здесь явно не годились, дети не могли с ними справляться, и надо было искать что-то иное, что могло быть одновременно доступным и для ребёнка-дошкольника, и для оканчивающего 10-й класс школы. К счастью, в нашей семье более десяти лет в качестве игрушки были в ходу кубики Косса (я нашёл в психологическом журнале 20-х годов описание этого теста и изготовил несколько наборов таких кубиков). Неизменный и многолетний интерес детей к этим кубикам, порождённый, видимо, оригинальной четырёхцветной окраской их граней и возможностью составлять огромное число самых разнообразных узоров, натолкнул на мысль разработать из них сначала развивающую игру "Сложи узор", а затем и тест, значительно совершеннее исходного.

Так появился тест для измерения "продуктивности умственной работы" детей (вариант 01.01.1974 г.). Он состоял из 15 задач, возрастающих по сложности, от доступных 3-летнему малышу до представляющих уже серьёзную трудность старшим детям и взрослым.

Подсчитав процент выполнения заданий и рекордные результаты на каждом (на 410 пробных испытуемых разного возраста), мне удалось хорошо ранжировать задания и определить меру сложности каждого в баллах.

Измерение продуктивности состояло в последовательном предъявлении узоров-заданий и фиксировании по секундомеру времени их выполнения. В протоколе записывалось "до которой из 15 ступенек испытуемый смог добраться" и какое время на это затратил (за какое время успел сложить из кубиков узор, подобный узору-заданию). Общее количество выполненной работы измерялось суммой баллов Сб, полученной за выполненные задания (от 0 до 60), а продуктивность ПУР рассчитывалась по формуле: Пур = Сб х Сtрек / Сtфакт, где Сtрек – сумма рекордных времён по каждому из выполненных заданий, а Сtфакт – сумма фактически затраченного времени на все выполненные задания.

Тест был хорош в нескольких отношениях:

1. Не требовал никакого предварительного обучения, и результат не зависел от какой-либо обученности, то есть даже неграмотный дошкольник мог справиться с простейшими заданиями.

2. Требовал сравнительно мало времени (в среднем 5-10 минут) на одного ребёнка.

3. Позволял легко и быстро подсчитывать результаты измерений.

4. Результаты измерений не только часто, но и почти полностью совпадали с оценкой способностей ребёнка, данной воспитателем или учителем (пусть не строгое, но для практики достаточное доказательство валидности теста).

Пробные попытки применить тест для измерения продуктивности целых групп детей в детском саду и классов в школе обрадовали меня результатами. Во-первых, средние значения продуктивности группы детей давали малый разброс, то есть первый класс в конце года или дети в возрасте 8 лет в любой школе давали один и тот же результат (около 3 баллов по моей шкале); во-вторых, результаты детей от 3 до 8 лет ложились по кривой, близкой к экспоненте, а далее шли почти по прямой линии, то есть экспериментальная кривая была близка по форме к кривой развития творческих способностей. Выходило, что найден "инструмент" измерения "творческого компонента" способностей ребёнка, достаточно совершенный для применения на практике.

Позже, в 1979 году, мне удалось испытать его в школе № 587 (Москва) в классе учительницы Софьи Николаевны Лысенковой, у которой дети учатся необычно радостно и увлечённо и не только хорошо подготовлены (показывают хорошие знания), но и высоко развиты. Какую разницу в продуктивности работы покажет класс в сравнении с нормой?

В 1-м "В" классе было 33 ученика, средний возраст их – 8 лет, а продуктивность их работы оказалась как у 9-летних. Значит, дети её класса получили за год такое развитие, какое другие приобретают за 2 года.

Второе такое измерение в 1984 году, но уже в 3-м "В" классе С.Н. Лысенковой поразило ещё больше: 23 ученика, средний возраст которых был 10 лет, показали такую продуктивность, на какую способны дети в 12,5 года. Значит, можно, несмотря на НУВЭРС, не менее чем вдвое быстрее развивать "творческий компонент" способностей. Значит, современная методика работы в начальной школе может быть усовершенствована, и весьма значительно. Жаль только, что меру этого совершенства никто больше не измеряет и удивительные успехи учительницы С.Н. Лысенковой известны немногим.

Но для построения сравнительного графика пришлось проделать огромную работу. За два с половиной года тест позволил измерить продуктивность 1400 детей в возрасте от 3 до 17 лет. Измерениям подвергались целые группы детского сада или школьные классы. Рассчитывалась средняя продуктивность каждой возрастной группы (линия "средние"), и выписывался самый лучший из результатов (линия "способные") и самый худший из результатов (линия "неспособные"). По ним построен экспериментальный график.

По оси абсцисс отложен возраст детей, по оси ординат – "продуктивность умственной работы". За единицу измерений взят "средний результат взрослых" (показанный 107 испытуемыми и равный 12 баллам по тесту).

Так как у Г. Айзенка средний взрослый набирает 100 баллов и решает, например, 10 задач из 40, то это значит то же, что 12 баллов в тесте на продуктивность. Если решает вдвое больше (20 задач), то Айзенк оценивает его результат в 125 баллов, а в тесте на продуктивность вдвое более высокому результату даётся 24 единицы. Так удалось совместить обе шкалы и, пусть не очень точно (погрешность порядка 10%), но для практики достаточно приемлимо, сравнить кривые развития детей при "традиционном" и "раннем" развитии. Для четвертой кривой точки взяты из сводной таблицы коэффициентов интеллектуальности.

Может, конечно, возникнуть вопрос: почему не проверил автор и своих детей по тесту на продуктивность, чтобы не надо было совмещать разные системы проверки? Такая проверка была бы неправомерной – дети много лет играли кубиками Косса, и это давало им огромное преимущество перед теми, кто эти кубики видел впервые. Пробные проверки подтвердили это предположение, и поэтому результаты не приводятся. А допущение, что продуктивность умственной работы пропорциональна общему уровню способностей, можно сделать с большим основанием. Если мы считаем, что "скорость протекания умственных процессов есть фундаментальный базис интеллектуальных различий между людьми", то какими бы способами мы ни измеряли эту скорость, мы должны получать одинаковый результат, если наша методика объективна.

Тест на продуктивность определяет эту скорость как "количество умственной работы" за измеренный промежуток времени, а у Айзенка даётся стандартный отрезок времени (30 минут) и считается число задач, решённых за это время (а даётся их в 4-5 раз больше того, что может решить средний взрослый). Совмещение 100 баллов с 12 баллами продуктивности и есть признание, что "скорость протекания умственных процессов" у среднего взрослого является постоянной величиной, хотя бы на период измерения.

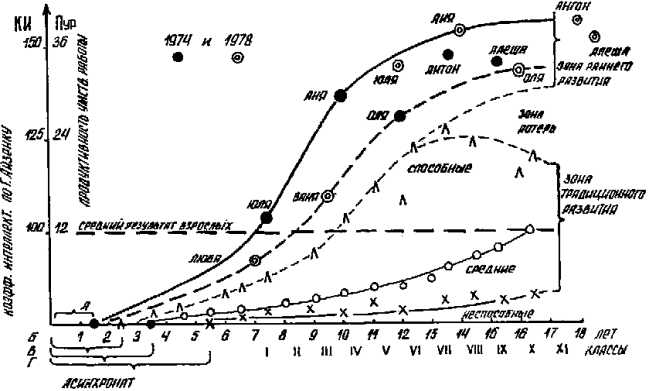
Рис. 9. ЭКСПЕРИМЕНТАЛЬНЫЙ ГРАФИК ПРОДУКТИВНОСТИ УМСТВЕННОЙ РАБОТЫ (Пур) ДЕТЕЙ, РАЗВИВАВШИХСЯ "ТРАДИЦИОННО" (1400 чел.), И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ "ОБЩЕГО УРОВНЯ СПОСОБНОСТЕЙ" ПО Г. АЙЗЕНКУ СЕМЕРЫХ ДЕТЕЙ НИКИТИНЫХ 1974-1978 гг.

Что говорит экспериментальный график?

1. Что некоторые положения гипотезы получают экспериментальное подтверждение. Схема влияния "условий" на процесс развития способностей и схема "влияния асинхроната", нарисованные чисто умозрительно 15 лет тому назад, объединились в реальные кривые развития, полученные при самых разных условиях и различной величине асинхроната. Хотя трактовать форму кривых можно и иначе: "условия" развития, возможно, влияют незначительно, а вот величина "асинхроната" имеет решающее значение:

· при малом асинхронате "а" мы получаем "раннее развитие и высокий уровень", почти в 3 раза превышающий "средний";

· при большем асинхронате "б" получаются "способные" только в 2 раза превышающие "средний";

· при асинхронате "в" получим уже "средний";

· при асинхронате "г" – только 40% "среднего".

Допустив, что "оптимальный срок начала развития" находится где-то рядом с днём рождения ребёнка (данных для такого допущения накопилось уже много), мы получим реальные величины асинхроната:

"а" –1,5 года,

"б" – 2,5 года,

"в"– 3,5 года,

"г"– 5,5 года.

Этими величинами асинхроната уже можно пользоваться для решения практических задач развития детей. Они могут дать родителям и воспитателям ориентиры, чего ожидать от ребёнка, откладывая начало развития на 2 или 3 года или на 6-7 лет, то есть перекладывая его целиком на школу.

2. Даже небольшое сокращение асинхроната и улучшение "условий" развития, достигнутые в нашей семье, позволило самым обычным детям, и всем семерым, подняться выше "способных".

Если среди "способных" только 9-летние достигают "среднего результата взрослых", то наши поднимались до этого уровня в 8 и даже в 7 лет.

3. Характер кривых также говорит о том, что наиболее благоприятно школьная учёба влияет на "неспособных". Хотя они развиваются медленно, их развитие непрерывно ускоряется до окончания 10 классов.

Развитие "средних" идёт почти линейно, а несколько ускоряется только до 10-11 лет.

Самая тревожная кривая развития у "способных" детей. Стремительный экспоненциальный взлёт в первые годы вдруг прекращается и с 13 лет кривая не только не поднимается вверх, а начинает даже опускаться. Какие причины могут приводить к этому? Главная – видимо, одна – неприспособленность самой школы для способных детей. Программы, методики и темпы умственной работы в школе не могут быть рассчитаны даже на "средних", так как тогда слабая половина или четверть класса не будут успевать. Видимо, они ориентируются на "слабых", чтобы успевали все ученики в классе. А продуктивность "способных" в умственной работе в 5-15 раз превосходит продуктивность "неспособных" (это видно из кривых), они "работают" в 1/5 или 1/10 своих возможностей, и... рост их останавливается.

Это очень тревожное явление. Значит, школа тормозит самых лучших, самых многообещающих, лишает их возможности расцветать уже с 13 лет. Поэтому возмутительно утверждение – "вундеркинды нас не радуют". Надо не способных детей винить и не их раннее развитие, а понять, что они не имеют не только оптимальных, но даже просто удовлетворительных условий для развития своих выдающихся к этому времени способностей.

4. Наши дети, сдвинутые к "раннему" развитию, тоже не избежали задержки, но она сказалась значительно меньше, чем у "способных". Видимо, имело значение то, что шестеро из них поступали в школу раньше, "перепрыгивали" через классы в середине года и сокращали время пребывания в ней на год, два или три.

5. Концы кривых образуют зоны: "зону традиционного развития", "зону потерь" и не ограниченную сверху "зону раннего развития". Первая говорит о широте диапазона в продуктивности умственной работы выпускников современной школы. "Способные" могут превосходить "средних" и в полтора, и в два раза, а "неспособных" даже в 4-5 раз. Но это положение будет существовать, пока есть "зона потерь". Если же она будет ликвидирована и воспитательная практика начнёт сдвигаться к "раннему" развитию и учитывать возможности "способных", то пределов роста творческих способностей человека мы не видим, да и вряд ли они существуют.

Мы понимаем, что наш "семейный эксперимент" далёк от требований научной строгости, так как шёл в условиях, оставляющих желать лучшего, и проверялся ограниченными средствами, и наши результаты в развитии детей и их способностей – только маленький шаг к раскрытию громадных возможностей человеческого разума. Но если даже в этих условиях развитие детей оказалась сравнительно высоким, то каких же удивительных успехов можно ожидать от эксперимента, поставленного на серьёзную научную и материальную основу.