Сравнительная характеристика методов

Характеристика	Метод частичного перебора	Алгоритм А*
Тип метода	Точный	Эвристический
Найденное решение	Оптимальное	Хорошее (может быть оптимальным)
Обход дерева	Поиск в глубину	Поиск в ширину
Потребные временные и вычислительные ресурсы	Больше	Меньше

3.2. Лабораторная работа № 7
Решение оптимизационной задачи
с использованием эвристического алгоритма

Цель работы:освоение точного и эвристического методов решения оптимизационной задачи.

Описание задачи и пример ее решения

А. Описание задачи

Между станциями А и Б имеется железнодорожный путь сообщения (рис. 30). На нем действует ряд ограничений скорости движения поездов. Каждое дополнительное ограничение скорости приводит к тому, что на проход поезда по участку затрачиваются дополнительное время, топливо (электроэнергия) и эксплуатационные расходы. Соответственно, если устранить эти ограничения, то дорога будет получать доход, равный сумме затрачиваемых расходов. Для получения максимального дохода (сведения дополнительных затрат к нулю) требуется устранить все ограничения скорости. Но так как дорога обладает ограниченными финансовыми возможностями (выделяемым объемом капитальных вложений), одновременное устранение всех ограничений невозможно. Кроме этого, могут быть определены другие требования на выбор мероприятий, направленных на устранение ограничений скорости. Например: срок окупаемости плана мероприятий должен быть не менее заданного; подразделения, выполняющие мероприятия, должны освоить определенный минимальный объем капвложений и т. д.

Б. Исходные данные

Примем, что по железнодорожному пути выполняется ежесуточный пропуск 10 однотипных грузовых поездов (N_гр.п = 10 шт.). На пути действует
6 дополнительных ограничений скорости. Скорости движения поезда с учетом и без учета ограничений скорости показаны на рис. 30.

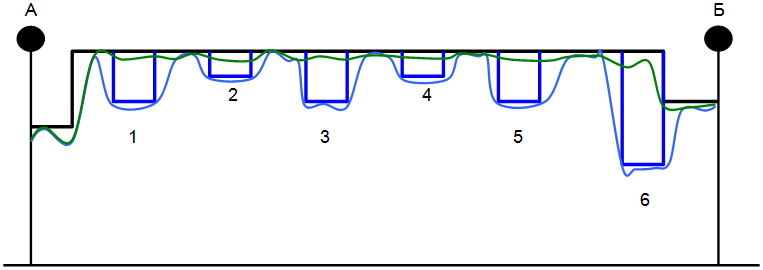
Рис. 30. Ограничения скорости и скорости движения поезда: – допускаемая скорость движения поезда без учета дополнительных ограничений; – дополнительные ограничения скорости; – скорость движения поезда без учета дополнительных ограничений; – скорость движения поезда с учетом дополнительных ограничений

Характеристика дополнительных ограничений скорости и соответствующих мероприятий по их устранению приведена в табл. 9. Мероприятия отсортированы по сроку окупаемости, т. е. в начале таблицы показаны мероприятия, дающие максимальный эффект (максимальную отдачу от капвложений).

Таблица 9

Характеристика дополнительных ограничений скорости
и мероприятий по их устранению

№ ограни-чения	Причина ограничения (мероприятие по устранению ограничения)	Дополни-тельные эксплуатацион­ные расходы на проход одного поезда DCi, руб.	Потребные капвложения на устра-нение ограничения Ki, руб.	Срок окупае-мости Токi, лет	Подразде-ление, выполняющее мероприятие
	Кривая малого радиуса R = 300 м (увеличение радиуса R = 1000 м)		2 000 000	2.2	ПМС-219
	Кривая малого радиуса R = 350 м (увеличение радиуса R = 1000 м)		2 500 000	3.4	ПМС-219
	Деформация опоры моста (укрепление опоры моста)		3 500 000	4.8	МСО-9

Окончание табл. 9

№ ограни-чения	Причина ограничения (мероприятие по устранению ограничения)	Дополни-тельные эксплуатацион­ные расходы на проход одного поезда DCi, руб.	Потребные капвложения на устра-нение ограничения Ki, руб.	Срок окупае-мости Токi, лет	Подразде-ление, выполняющее мероприятие
	Дефект трубы (замена оголовка трубы)		4 500 000	4.9	МСО-9
	Кривая малого радиуса R = 400 м (увеличение радиуса R = 1200 м)		4 200 000	7.7	ПМС-219
	Дефект трубы (замена оголовка трубы)		5 000 000	10.5	МСО-9

Примечание. Срок окупаемости отдельного мероприятия применительно к рассматриваемой задаче рассчитывается по формуле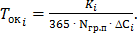

В качестве подразделений, которые могут выполнять мероприятия, выбраны:

· ПМС-219 – путевая машинная станция, выполняющая работы по земляному полотну и верхнему строению пути;

· МСО-9 – мостостроительный отряд, выполняющий работы по искусственным сооружениям.

В.Постановка задачи

Составить план (выбрать) мероприятий, направленных на устранение дополнительных ограничений скорости, чтобы капитальные вложения в мероприятия плана окупились в минимально короткий срок (принесли максимальный доход) при безусловном выполнении заданных требований на характеристики плана (решение задачи).

Срок окупаемости всего плана мероприятий рассчитывается по формуле

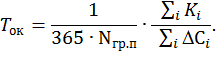
В качестве требований к характеристикам плана выступают следующие:

· суммарные капвложения не должны превышать 12 000 000 руб.;

· ПМС-219 должна освоить не менее 3 000 000 руб.;

· МСО-9 должен освоить не менее 4 500 000 руб.

Таким образом требуется найти план с минимальным сроком окупаемости

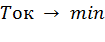
с учетом следующих условий:

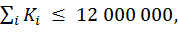(О₁)

где i соответствует мероприятиям, включенным в план;

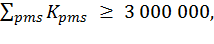(О₂)

где pms соответствует мероприятиям, включенным в план и выполняемым ПМС-219;

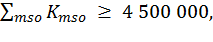(О₃)

где mso соответствует мероприятиям, включенным в план и выполняемым МСО-9.

Г.Решение задачи методом частичного перебора

Дерево поиска решения методом частичного перебора показано на рис. 31.

Обход дерева выполняется сверху вниз слева направо (поиск в глубину). Каждый узел дерева (за исключением корневого) соответствует набору мероприятий. M_i = 1 означает включение i-го мероприятия в план,
M_i = 0 – невключение. Соответственно план мероприятий для каждого узла включает в себя все мероприятия, для которых M_i = 1, начиная с корневого и до текущего узла при спуске по стрелкам. Включение мероприятий в план согласно табл. 9 обеспечивает монотонность возрастания критерия (срока окупаемости). Надпись O_j означает несоблюдение j-го требования.

Характеристика найденного оптимального решения (плана) включает:

· мероприятия 1, 5 и 6;

· потребные капвложения менее максимально выделяемого объема 9 000 000 ≤ 12 000 000;

· объем капвложений, осваиваемых ПМС-219, не менее минимально потребного 4 500 000 ≥ 3 000 000;

· объем капвложений, осваиваемых МСО-9, не менее минимально потребного 4 500 000 ≥ 4 500 000;

· срок окупаемости плана мероприятий T_ок = 3,5 года.

Рис. 31. Дерево поиска решения методом частичного перебора: узел с тонкой одинарной рамкой – промежуточное решение, неудовлетворяющее требованиям O2 или О3, из которого: имеет смысл дальше искать оптимальное решение (ниже расположены узлы, обозначенные большими квадратами); не имеет смысла дальше искать оптимальное решение, так как до этого уже было найдено допустимое решение с меньшим сроком окупаемости Ток (ниже расположены узлы, обозначенные малыми квадратами с одинарной штриховой рамкой). При дальнейшем поиске решения из этого узла, даже если будет найден новый допустимый вариант плана, значение срока окупаемости по нему будет заведомо хуже найденного; узел с толстой одинарной рамкой и белым фоном – допустимое, но не оптимальное решение; узел с толстой одинарной рамкой и серым фоном – оптимальное решение; узел с двойной рамкой – недопустимое решение. Нарушено требование на суммарные капвложения O1. Добавление мероприятий в такой план приведет к еще большему нарушению этого требования. Несоблюдение требований O2 и O3 (на минимальные суммарные капвложения, осваиваемые конкретными подразделениями) в отличие от требования O1 не означает прекращения поиска решения из конкретного узла; узел с одинарной штриховой рамкой – решение, не требующее рассмотрения (не попавшее в обход дерева)

Д.Решение задачи с использованием алгоритма А*.

Дерево поиска решения с помощью алгоритма А* показано на рис. 32.

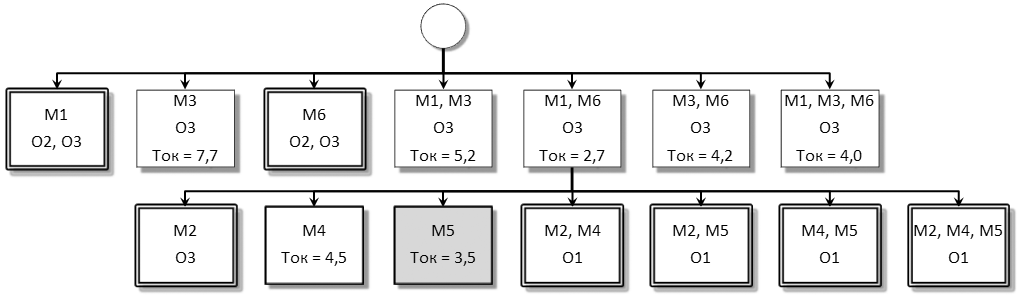
Рис. 32. Дерево при поиске решения с использованием алгоритма А*

Одним из вариантов решения задачи с использованием алгоритма А* является перебор возможных планов, когда на каждом уровне дерева рассматриваются сочетания мероприятий, выполняемые одним подразделением.

Надписи, цвет фона и тип рамки узлов приняты, как и при решении задачи методом частичного перебора. На 1-м уровне вариант плана должен обязательно отвечать требованиям O₁ и O₂, а на 2-м уровне – всем требованиям. В связи с этим, в узлах, несоответствующих этим требованиям, расчет критерия (срока окупаемости Т_ок) не выполняется.

Толстой одинарной рамкой и серым фоном выделен узел, соответствующий оптимальному плану. Результат (оптимальный план) идентичен полученному с помощью метода частичного перебора и состоит из мероприятий 1, 5 и 6.

Если бы из узла 1-го уровня с мероприятиями 1 и 6 все продолжения вели бы к узлам 2-го уровня, для каждого из которых не соблюдалось хотя бы одно требование, тогда при поиске решения следовало бы рассмотреть продолжения из следующего по оптимальности узла 1-го уровня (на рис. 32 узел с мероприятиями 1, 3 и 6) и т. д.

Следует отметить, что в данном конкретном случае алгоритм А* оказался эффективнее метода частичного перебора (при одинаковом результате потребовалось меньше вычислений). В то же время, если бы количество мероприятий, выполняемых ПМС-219, было бы не три, а десять, то уже на 1-м уровне пришлось бы рассматривать 1023 варианта вместо 7.

Задание на выполнение работы

Определить план выполнения мероприятий по ликвидации дополнительных ограничений скорости с помощью метода частичного перебора и алгоритма А*.

А. Набор требований к параметрам плана:

· суммарные капвложения не должны превышать 12 000 000 руб.;

· ПМС-219 должна освоить не менее 3 000 000 руб.;

· МСО-9 должен освоить не менее 4 500 000 руб.

Б. Индивидуальный вариант задания выбрать согласно табл. 10. Остальные исходные данные принять такими же, как и в рассмотренном выше примере.

Таблица 10

Варианты заданий на выполнение лабораторной работы

№ варианта

DCi, руб., для ограничения

Ki, руб., для ликвидации ограничения (выполнения мероприятия)

В.Отчет должен содержать:

· титульный лист;

· краткое описание постановки задачи, включая перечень требований и номер варианта;

· таблицу с мероприятиями, отсортированными по сроку окупаемости, аналогичную табл. 9;

· полное дерево решений при поиске оптимального плана с помощью метода частичного перебора (см. рис. 31);

· полное дерево решений при поиске эффективного плана с использованием алгоритма А* (см. рис. 32);

· вывод об эффективности и корректности поиска решения двумя способами.

Контрольные вопросы

1. Дайте определение математических понятий «граф» и «дерево».

2. Что понимается под эвристическим методом решения задачи?

3. назовите условия (ограничения) применимости метода частичного перебора.

4. В каких случаях в методе частичного перебора не ведется поиск оптимального решения из текущего узла в направлении нижележащих
(по исходящим ветвям)?

5. Дайте сравнительную характеристику метода частичного перебора
и алгоритма А*.

НЕЧЕТКИЕ МНОЖЕСТВА