Два принципа интуитивной теории множеств
Введение в теорию множеств
Основные понятия и определения теории множеств
Определение.Под множеством (совокупностью) М понимают набор объектов произвольной природы, которые называются элементамимножества. Если число элементов конечно, множество называется конечным. В противном случае говорят о бесконечном множестве.
Подразумевается, что элементы множества различны и различимы между собой. Само множество элементов рассматривается как единое целое, и в качестве такого может быть элементом любого другого множества. Элементы могут быть любыми объектами - числами, людьми, яблоками, буквами и тому подобное. В математике в качестве элементов множества рассматривают математические объекты - числа и множества чисел, точки и множества точек, абстрактные элементы, образующие алгебраические структуры: группы, поля, кольца, решетки и т.д.
Множества большей частью будем обозначать большими латинскими буквами: А, М, Х. Для числовых множеств приняты такие обозначения
N - множество натуральных чисел;
N+ - множество натуральных чисел с нулем;
Z - множество целых чисел;
Q - множество рациональных чисел;
R - множество вещественных чисел;
C - множество комплексных чисел.
Все перечисленные числовые множества бесконечны.
Постулируется, что любое множество состоит из своих элементов и однозначно определяются ими. Таким образом, предполагается, что для каждых конкретных объекта и множества можно определить, является ли данный объект элементом данного множества или нет. Элементы множества будем обозначать малыми латинскими буквами: а, b, … , x, y, z.
Определение. Говорят, что всякий элемент х множества М принадлежит М и пишут: хÎМ. Если же предмет х не является элементом множества М, то говорят, что х не принадлежит М и пишут: хÏМ.
Если множество А состоит из элементов а1, а2, … , ап, будем писать: а1, а2, … , ап Î А или А = {а1, а2, … , ап}. При этом порядок перечисления элементов не имеет значения.
Определение. Множества, содержащие в качестве элементов другие множества, называются семействами (классами).
Определение. Множество, не содержащее ни одного элемента, называется пустым и обозначается 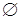 . Существование пустого множества – это постулат.
. Существование пустого множества – это постулат.
Определение. Если все элементы данной системы множеств принадлежат какому-то одному большому множеству, такое множество называется универсальным множеством или универсумом и обозначается U. Из контекста, как правило, ясно, какие элементы образуют универсум. В иных случаях универсум - это некоторое абстрактное множество, из элементов которого состоят все остальные множества, и других «кирпичиков» для образования множеств нет.
Два принципа интуитивной теории множеств
Утверждение, что любое множество однозначно определяется своими элементами можно сформулировать по-другому.
Определение. (Интуитивный принцип объемности). Два множества А и В называются равными, пишется A = B, тогда и только тогда, когда они состоят из одних и тех же элементов.
Следовательно, если множества А и В не равны, то существует хотя бы один элемент х такой, что х принадлежит одному из этих множеств, но не принадлежит другому. Неравенство множеств обозначается символом 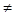 ,пишут A
,пишут A 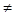 B.
B.
В соответствии с принципом объемности доказательство равенства множеств А и В нужно проводить в два этапа: доказать, что всякий элемент 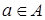 принадлежит также множеству В; доказать, что всякий элемент
принадлежит также множеству В; доказать, что всякий элемент 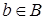 принадлежит и множеству А.
принадлежит и множеству А.
Пример 1.МножествоА = {1, 2, 3} равно множеству В = {2, 3, 1}, так как порядок перечисления элементов множества не имеет значения.
Пример 2. 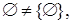 множество слева от знака ¹ – это пустое множество, не содержащее элементов, а множество справа – это множество, содержащее единственный элемент – пустое множество.
множество слева от знака ¹ – это пустое множество, не содержащее элементов, а множество справа – это множество, содержащее единственный элемент – пустое множество.
Пример 3. {{1, 2}, {2, 3}} ¹ {1, 2, 3}, так как первое множество – это семейство, содержащее два элемента: множества {1, 2}, {2, 3}. Второе множество содержит три элемента – 1, 2, 3.
Определение. Под высказыванием будем понимать любое повествовательное предложение, которое можно охарактеризовать как истинное или ложное.
Под одноместным характеристическим предикатом от 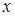 будем понимать некоторое утверждение относительно объекта
будем понимать некоторое утверждение относительно объекта 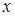 , которое превращается в высказывание, истинное, ложное или бессмысленное, если букву
, которое превращается в высказывание, истинное, ложное или бессмысленное, если букву 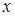 заменить именем объекта.
заменить именем объекта.
Сразу оговоримся, что судить об истинности, ложности или бессмысленности полученного высказывания можно не всегда. Но сейчас мы приведем примеры одноместных предикатов, для которых такие суждения представляются возможными.
1. Рассмотрим утверждение « 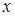 > 5». Этот предикат превращается в истинное высказывание, если букву
> 5». Этот предикат превращается в истинное высказывание, если букву 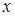 заменить числом 8, ложное высказывание, если букву
заменить числом 8, ложное высказывание, если букву 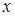 заменить числом 4 и, по-видимому, в бессмысленное высказывание, если написать «слон > 5».
заменить числом 4 и, по-видимому, в бессмысленное высказывание, если написать «слон > 5».
2. Предикат «слово 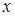 содержит букву б» превращается в истинное высказывание в случае «слово «алгебра» содержит букву б» и ложное в случае «слово «группа» содержит букву б».
содержит букву б» превращается в истинное высказывание в случае «слово «алгебра» содержит букву б» и ложное в случае «слово «группа» содержит букву б».
Частично избежать бессмыслицы можно, если заранее оговорить, из какого множества выбираются имена, заменяющие букву 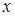 3.
3.
Всякий одноместный предикат можно считать функцией одного переменного х. Значения функции – истинные ложные или бессмысленные высказывания. Область определения – некоторое множество имен объектов.
Понятие одноместного предиката легко обобщить, определяя двух-, трех-,…, n- местные предикаты. Например, “x+y=5” – это двухместный предикат , “x+y=z” – трехместный предикат и т.д.
Предикаты будем обозначать большими латинскими буквами, после которых в скобках перечислены их аргументы: P(x), Q(x, y), R(x1, x2, …, xn) и т.д.
