Текущая (приведенная) стоимость. Экономическая сущность дисконтирования

Приведенная стоимостьбудущего платежа - это стоимость платежа, как если бы его произвели немедленно. Будущая стоимостьплатежа, совершаемого сегодня, - это стоимость платежа исходя из предположения, что его произвели через какое-то время в будущем.

Приведенная стоимость банковского вклада составляет 1000 долл. Если владелец средств размещает их на вклад на два года под 6% годовых с ежегодным начислением процентов на всю сумму вклада, то через два года сумма средств на счете составит 1123,60 долл. Это будущая стоимость вклада на сумму 1000 долл., размещенную на два года под 6% годовых.

Процентная ставка и промежуток времени между текущим и будущим платежом математически связывают приведенную и будущую стоимость. Обозначим приведенную стоимость как PV, а будущую стоимость как FV. Тогда общая зависимость между буду-щей и текущей стоимостью имеет следующий вид:

FV= PV(1 + r)n.

Термин дисконтирование в широком смысле означает определение значения стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину.
Рис. 6. Логика финансовой операции дисконтирования.

Не редко такой расчет называют приведением стоимостного показателя к заданному моменту времени, а величину PV называют приведенной (современной или текущей) величиной FV. Таким образом, дисконтирование – приведение будущих денег к текущему моменту времени, и при этом не имеет значения, имела ли место в действительности данная финансовая операция или нет, а также независимо от того, можно ли считать дисконтируемую сумму буквально наращенной.

Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции.

Будущая стоимость. Таблицы значений будущей стоимости.

Чем чаще периодичность начисления процентов на процент, тем быстрее растет приведенная стоимость. Чтобы проиллюстрировать этот принцип, давайте рассчитаем будущую стоимость исходного вклада на сумму 1000 долл., размещенного под 12% годо-вых с начислением процентов на процент каждые полгода. При начислении процентов на процент каждые полгода мы прибавляем сумму процентных начислений за первые полго-да к основной сумме вклада, и полученная сумма становится основной, на которую начис-ляется процент по истечении следующих шести месяцев. Так как процентная ставка со-ставляет 12% годовых, то за полгода начисляется 6%. То есть через первые шесть месяцев сумма средств на счете составит 1060 долл. == 1000(1 + 0,12/2). Когда на эту сумму в 1060 долл. начисляется процент попрошествии следующих шести месяцев, то сумма средств на счете вырастает до 1123,60 долл. = 1060(1 + 0,12/2). То есть через год при начислении процентов на процент каждые полгода исходный вклад на сумму 1000 долл. имеет стои-мость в 1123,60 долл.

Существует и более прямой способ расчета будущей стоимости, при котором ис-ходят из того, что 1000 долл. вкладываются на два периода, каждый продолжительностью шесть месяцев, при этом ставка составляет 6% за период. На основании этих данных фор-мулируется задача по определению будущей стоимости (процентная ставка - 6% за пери-од; количество периодов - 2). В более общем виде, если в году имеется (т) периодов на-числения сложного процента, то по истечении (n) лет при годовой процентной ставке (r) процентов стоимость FV можно рассчитать по следующей формуле:

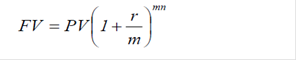
В качестве варианта расчета будущей стоимости единичных платежей согласно формуле будущей стоимости можно применять таблицы значений будущей стоимости, которые приведены в приложении к данной книге. В таблице 2.2 воспроизведена часть этих таб-лиц, с тем чтобы показать, как их применять.

Таблица 2.2

Будущая стоимость 1 долл.

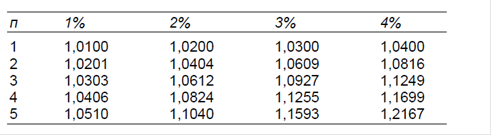Предположим, что вы хотите знать будущую стоимость 2000 долл. через три меся-ца от настоящей даты при ставке 2% в месяц. Согласно таблице 2.2 будущая стоимость 1 долл., размещенного под 2% за период сроком на 3 периода, составляет 1,0612. Это коэф-фициент приведения к будущему времени вложений настоящего времени при ставке в 2% и числе периодов, равном 3. Нас же интересует будущая стоимость 2000 долл., а не 1 долл., поэтому мы просто умножаем 2000 долл. на данный коэффициент. Отсюда будущая стоимость этой суммы составляет 2000 х 1,0612 = 2122,40 долл.

Обратите внимание, что ставка процента, используемая в таблицах, необязательно является годовой процентной ставкой. Аналогично, число периодов необязательно есть число годовых периодов. В нашем примере мы использовали месячные ставки и периоды, равные одному месяцу. Вам необходимо помнить важное правило, которое гласит, что временные периоды должны быть всегда выражены в тех единицах, которые согласуются с процентной ставкой. Например, если каждый период равен одному месяцу, то и про-центная ставка должна быть выражена как месячная процентная ставка.