Свойства геометрических фигур (вычисления).

1. В параллелограмме АВСD угол А равен 60°, а его биссектриса делит сторону ВС на отрезки, равные 4 см и 6 см. Найдите площадь параллелограмма.

2. В треугольнике АВС длина стороны АС равна 20 см, медиана ВК перпендикулярна биссектрисе СD. Найдите длины двух других сторон треугольника, если его периметр равен 45 см.

3. Острый угол прямоугольной трапеции АВСD равен 45° .Меньшее основание трапеции равно меньшей боковой стороне. Найдите большее основание трапеции, если длина средней линии равна 3.

4. В квадрат со стороной 5 см вписан второй квадрат так, что его вершины являются серединами сторон первого квадрата. Во второй квадрат таким же образом вписан третий. Найдите сумму периметров всех трех квадратов.

5. В правильный треугольник со стороной 6 см вписан второй треугольник, вершинами которого являются середины сторон первого. Во второй треугольник таким же образом вписан третий. Найдите сумму периметров этих трех треугольников.

6. Боковые стороны и меньшее основание прямоугольной трапеции равны соответственно 8 см, 10 см, 10 см. Найти большее основание .

7.Два угла треугольника равны соответственно 55° и 67°. Найдите тупой угол между высотами, проведенными из вершин этих углов.

8. В остроугольном треугольнике АВС проведены высоты АК = 10 см, СЕ = 12 см. Отрезок ВЕ = 9 см. Найдите площадь треугольника.

9. Периметр прямоугольника АВСD равен 24 см. Точка М – середина стороны ВС, а МА и МD – взаимно перпендикулярные прямые. Найдите стороны прямоугольника.

10. В параллелограмме АВСD угол В тупой. На стороне АD отмечена точка Е так, что Ð ВЕА = 90°, Ð АВЕ = 45°, АЕ = 4 см, ЕD = 7 см. Найдите площадь параллелограмма.

11. Один из острых углов прямоугольного треугольника равен 60°, а сумма длин гипотенузы и меньшего из катетов – 27 см. Найдите длину гипотенузы.

12. В треугольнике один из углов равен 50°, второй – 70°. Найдите острый угол между высотами, проведенными из вершин этих углов.

13. Найдите площадь прямоугольного треугольника, если его катеты относятся как 3 : 4, а гипотенуза равна 25 см.

14. В параллелограмме АВСD угол В тупой. На продолжении стороны АD за вершину D отмечена точка Е так, что Ð СЕD = 90°, Ð ЕСD = 60°, АВ = 4 см, АD = 10 см. Найдите площадь параллелограмма.

15. Найдите площадь ромба со стороной 8 см, если угол между стороной ромба и его диагональю равен 60°.

16. Найдите площадь ромба со стороной 14 см, если угол между стороной ромба и его диагональю равен 22,5°.

17. Найдите сторону параллелограмма, если другая его сторона равна 8 см, его площадь 24 см², а один из углов 30°.

18. Найдите стороны параллелограмма, если его диагонали равны 8 см и 6 см, а угол между ними равен 60°.

19. Найдите площадь равнобедренного треугольника с основанием 16 см и боковой стороной 10 см.

20. Периметр равнобедренного треугольника равен 16 см. Найдите высоту, проведенную к основанию, если оно длиннее боковой стороны на 1 см.

21. В равнобедренном треугольнике боковая сторона равна 12 см, а угол при вершине равен 120°. Найдите периметр треугольника..

22. Найдите сторону ромба, площадь которого равна 24 дм², а одна из диагоналей 6 дм.

23. Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 8 м, периметр равен 44 м. Найдите площадь трапеции.

24. Средняя линия равнобедренной трапеции делится диагональю на части длиной 2 см и 5 см. Найдите площадь трапеции, если ее боковая сторона равна 5 см.

25. Средняя линия равнобедренной трапеции равна 20 см, высота 15 см. Найдите диагональ и боковую сторону трапеции, если ее основания относятся как 3 : 7.

22. Свойства геометрических фигур (доказательства).

Сделайте чертеж и докажите утверждение.

1. Вершины треугольника равноудалены от прямой, проходящей через середины двух его сторон.

2. Если точка К – середина медианы АМ треугольника АВС, а прямая ВК пересекает сторону АС в точке D, то АD = 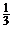АС.

3. Если в равнобедренном треугольнике АВС с основанием АС и углом при вершине В, равным 36°, проведена биссектриса АD, то треугольники СDА и АDВ – равнобедренные.

4. Отрезок АD – биссектриса треугольника АВС. Если через точку D провести прямую, параллельную АС и пересекающую сторону АВ в точке Е, то треугольник ADE – равнобедренный

5. Середины сторон равнобедренного треугольника являются вершинами равнобедренного треугольника.

6. Если диагонали прямоугольника пересекаются под прямым углом, то этот прямоугольник – квадрат.

7. АВСD – квадрат. Если на каждой его стороне отложить равные отрезки: АА₁ = ВВ₁ = СС₁ = DD₁, то А₁В₁С₁D₁ – также квадрат.

8. На диагонали АС квадрата АВСD отмечена точка М так, что АМ = АВ. Через точку М проведена прямая, перпендикулярная прямой АС и пересекающая сторону ВС в точке H. Доказать, что BH = HM = MC.

9. Выпуклый четырехугольник является параллелограммом, если его противоположные углы парами ровны.

10. Выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащих к каждой из двух смежных сторон, ровна 180°.

11. Диагонали параллелограмма АВСD пересекаются в точке О. Значит, четырехугольник А₁В₁С₁D₁, вершинами которого являются середины отрезков ОА, ОВ, ОС, ОD, – параллелограмм.

12. На диагонали ВD параллелограмма АВСD отмечены точки Р и М так, что РВ = МD. Значит, четырехугольник АРСМ – параллелограмм.

13. На сторонах АВ, ВС, СD и DА четырехугольника АВСD отмечены соответственно точки M, N, P и K так, что AМ = CP, BN = DK, BM = DP, NC = KA. Доказать, что ABCD и MNPK – параллелограммы.

14. Если из вершин В и D параллелограмма АВСD, у которого АВ ¹ ВС, а угол А – острый, провести перпендикуляры ВК и DМ к прямой АС, то получившийся четырехугольник ВМDК – параллелограмм.

15. Точки пересечения биссектрис углов параллелограмма образуют прямоугольник.

16. Если точки М и N – середины сторон АD и ВС параллелограмма АВСD, то прямые АN и МС делят диагональ ВD на 3 равные части.

17. Если в параллелограмме все углы равные, то это – прямоугольник.

18. Середины сторон прямоугольника являются вершинами ромба.

19. Середины сторон ромба являются вершинами прямоугольника.

20. Точка пересечения диагоналей ромба равноудалена от его сторон.

21. Из вершины В ромба АВСD проведены перпендикуляры ВК и ВМ к прямым АD и DС. Значит, луч ВD является биссектрисой угла КВМ.

22. В равнобедренной трапеции углы при основании равны.

23. Если в трапеции углы при основании равны, то она равнобедренная.

24. Если в трапеции диагонали равны, то она равнобедренная.

25. В равнобедренной трапеции диагонали равные.

23. Геометрические преобразования (осевая симметрия).

Заданы координаты вершин треугольника АВС.

Постройте D А₁В₁С₁ = S_l o S_р (D АВС).

Запишите координаты вершин треугольника А₁В₁С₁.

1. А (–3, 2), В (–6, 4), С (–2, 5), l – прямая у = х, р – прямая у = 1.

2. А (3, –2), В (–5, 4), С (–2, 3), l – прямая у = х, р – прямая у = 2.

3. А (–3, ­2), В (–6, 2), С (–1, 5), l – прямая у = х, р – прямая у = –1.

4. А (–2, 2), В (–4, 4), С (–2, 5), l – прямая у = х, р – прямая у = –2.

5. А (–1, 4), В (2, 4), С (–2, 5), l – прямая у = х, р – прямая у = 1.

6. А (–3, 2), В (–1, 4), С (–2, 5), l – прямая у = х, р – прямая у = –1.

7. А (–3, 1), В (–6, 3), С (–1, 5), l – прямая у = х, р – прямая у = 1.

8. А (–4, 2), В (–5, 4), С (–2, 4), l – прямая у = х, р – прямая у = – 1.

9. А (–3, 2), В (–6, 4), С (–2, 5), l – прямая у = – х, р – прямая у = 1.

10. А (–3, 2), В (–6, 4), С (–2, 5), l – прямая у = – х, р – прямая у = –1.

11. А (–3, 1), В (–6, 4), С (–2, 4), l – прямая у = – х, р – прямая у = 1.

12. А (–4, 2), В (–6, 3), С (–2, 5), l – прямая у = – х, р – прямая у = –1.

13. А (–3, 2), В (–5, 4), С (–1, 5), l – прямая у = – х, р – прямая у = 2.

14. А (–2, 2), В (–6, 4), С (–2, 4), l – прямая у = х + 1, р – прямая у = 1.

15. А (–3, 2), В (–6, 2), С (–3, 5), l – прямая у = х + 1, р – прямая у = –1.

16. А (–3, 2), В (–6, 3), С (–3, 5), l – прямая у = х + 1, р – прямая у = 2.

17. А (–4, 2), В (–5, 4), С (–2, 4), l – прямая у = х – 1, р – прямая у = 1.

18. А (–3, 4), В (–2, 4), С (–2, 5), l – прямая у = х – 1, р – прямая у = 2.

19. А (–3, 5), В (6, 4), С (–2, 5), l – прямая у = х – 1, р – прямая у = – 1.

20. А (3, –2), В (–6, 4), С (–2, 5), l – прямая у = х, р – прямая х = 1.

21. А (–3, –2), В (–6, 4), С (–2, 1), l – прямая у = х, р – прямая х = – 1.

22. А (–3, –1), В (–4, 4), С (–2, 0), l – прямая у = х, р – прямая х = 2.

23. А (3, 2), В (6, 4), С (2, 5), l – прямая у = х, р – прямая у = х + 1

24. А (3, 2), В (6, –4), С (–2, 5), l – прямая у = х, р – прямая у = х + 2.

25. А (–3, 2), В (–6, 4), С (–2, 5), l – прямая у = х, р – прямая у = х – 2.

24. Геометрические преобразования

(параллельный перенос, центральная симметрия).

Заданы координаты вершин четырехугольника АВСD.

Постройте четырехугольник А₁В₁С₁D₁ = Z_Р o (АВСD).

Запишите координаты вершин четырехугольника А₁В₁С₁D_1.

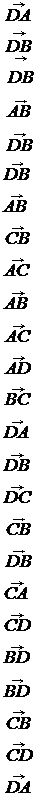1. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); =2 , Р (6, 6).

2. А (–3, 2), В (–5, 4), С (–2, 5), D (1, 2); = 2 , Р (6, –1).

3. А (–3, –1), В (–6, 4), С (–2, 4), D (1, 2); = 2 , Р (5, 1).

4. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); = 2 , Р (6, 0).

5. А (–3, 1), В (–5, 4), С (–2, 5), D (2, 2); = 2 , Р (5, 6).

6. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); = 2 , Р (–6, 6).

7. А (–3, 2), В (–4, 4), С (–2, 5), D (2, 2); = 2 , Р (–5, 6).

8. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); = 2 , Р (6, –6) .

9. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); = 2 , Р (5, 4).

10. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); = 2 , Р (3, 6).

11. А (–3, 1), В (–6, 4), С (–2, 5), D (1, 2); = 2 , Р (8, 6).

12. А (3, 1), В (6, –4), С (–2, 5), D (1, 2); = 2 , Р (8, 3).

13. А (–3, 1), В (6, 4), С (–2, 5), D (–1, 2); = 2 , Р (7, 6).

14. А (3, 1), В (–4, 4), С (–2, 5), D (1, –2); = 2 , Р (7, 5).

15. А (–3, 1), В (–3, 4), С (–2, 5), D (2, 2); = 2 , Р (7, 3).

16. А (–3, 1), В (–4, 4), С (–2, 5), D (1, 3); = 2 , Р (7, 1).

17. А (–4, 1), В (–2, 4), С (–2, 5), D (1, 2); = 2 , Р (8, –1).

18. А (–3, 1), В (–3, 4), С (–2, 5), D (3, 2); = 2 , Р (8, –2).

19. А (–3, 1), В (–1, 4), С (–2, 5), D (1, 1); = 2 , Р (8, –3).

20. А (–3, 1), В (6, –4), С (–2, 5), D (1, 1); = 2 , Р (–6, 2).

21. А (–2, 1), В (–1, 4), С (–2, 5), D (1, 2); = 2 , Р (–6, –6).

22. А (–3, 1), В (–1, 4), С (–2, 4), D (1, 2); = 2 , Р (–8, 2).

23. А (–1, 1), В (–4, 4), С (–2, 5), D (1, 2); = 2 , Р (–7, 1).

24. А (–3, 1), В (2, 4), С (–2, 5), D (–1, 2); =2 , Р (–7, –3).

25. А (–3, 1), В (0, 4), С (–2, 5), D (1, –2); = 2 , Р (–6, –5).

25. Геометрические преобразования (гомотетия, поворот).

Заданы координаты вершин треугольника АВС.

Постройте D А₁В₁С₁ = 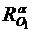o 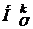(D АВС).

Запишите координаты вершин треугольника А₁В₁С₁.

1. А (–3, 1), В (–6, 4), С (–2, 5), О¢ (1, 2), О₁ (5, 2), k = –2, a = + 90°.

2. А (–2, 1), В (–5, 4), С (–2, 3), О¢ (2, 2), О₁ (1, 2), k = 2, a = – 90°.

3. А (–1, 1), В (–6, 4), С (–2, 5), О¢ (1, 1), О₁ (2, 2), k = –2, a = + 90°.

4. А (–4, 1), В (–5, 4), С (–2, 3), О¢ (–1, 2), О₁ (3, 2), k = 2, a = – 90°.

5. А (–5, 1), В (–6, 4), С (–2, 5), О¢ (1, 2), О₁ (4, 2), k = –2, a = + 90°.

6. А (–4, 1), В (–5, 4), С (–2, 3), О¢ (–1, 2), О₁ (1, 1), k = 2, a = – 90°.

7. А (–3, 1), В (–6, 4), С (–2, 5), О¢ (1, 2), О₁ (1, 2), k = –2, a = + 90°.

8. А (–2, 1), В (–5, 4), С (–2, 3), О¢ (–1, 2), О₁ (1, 3), k = 2, a = – 90°.

9. А (–1, 1), В (–6, 4), С (–2, 5), О¢ (1, 2), О₁ (1, 4), k = –2, a = + 90°.

10. А (–3, 1), В (–5, 4), С (–2, 3), О¢ (1, –2), О₁ (1, 5), k = 2, a = – 90°.

11. А (–3, 2), В (–6, 4), С (–2, 5), О¢ (1, 0), О₁ (1, 1), k = –2, a = + 90°.

12. А (–3, 3), В (–5, 4), С (–2, 3), О¢ (–1, 2), О₁ (1, 2), k = 2, a = – 90°.

13. А (–3, 4), В (–6, 4), С (–2, 5), О¢ (–2, 2), О₁ (1, 3), k = –2, a = + 90°.

14. А (–3, 5), В (–5, 4), С (–2, 3), О¢ (3, 2), О₁ (1, 4), k = 2, a = – 90°.

15. А (–3, –1), В (–6, 4), С (–2, 5), О¢ (3, 0), О₁ (1, 1), k = –2, a = + 90°.

16. А (–3, –2), В (–5, 4), С (–2, 3), О¢ (0, 3), О₁ (2, 2), k = 2, a = – 90°.

17. А (–2, –1), В (–6, 4), С (–2, 5), О¢ (1, 4), О₁ (3, 3), k = –2, a = + 90°.

18. А (–3, 0), В (–5, 4), С (–2, 3), О¢ (–1, 0), О₁ (4, 4), k = 2, a = – 90°.

19. А (3, –1), В (–5, 4), С (–2, 5), О¢ (–1, 4), О₁ (1, 2), k = –2, a = + 90°.

20. А (2, 1), В (–6, 4), С (–2, 3), О¢ (4, 0), О₁ (1, –2), k = 2, a = – 90°.

21. А (3, 0), В (–5, 4), С (–2, 5), О¢ (3, 0), О₁ (1, 2), k = –2, a = + 90°.

22. А (3, 1), В (–6, 4), С (–2, 3), О¢ (1, 4), О₁ (–2, 2), k = 2, a = – 90°.

23. А (3,2), В (–5, 4), С (–2, 5), О¢ (4, 4), О₁ (–1, 2), k = –2, a = + 90°.

24. А (–4, 2), В (–6, 4), С (–2, 3), О¢ (–3, 4), О₁ (–1, 0), k = 2, a = – 90°.

25. А (0, 4), В (–6, 4), С (–2, 5), О¢ (–3, 0), О₁ (0, 2), k = –2, a = + 90°.