Усеченное нормальное распределение. Усеченное нормальное распределение получают из обычного нормального закона в тех случаях, когда средняя наработка до отказа tН мала относительно среднего
Усеченное нормальное распределение получают из обычного нормального закона в тех случаях, когда средняя наработка до отказа tН мала относительно среднего квадратического отклонения s: tН<2s. В этом случае "неучет" плотности вероятности f(t), при "отрицательном" времени дает значительную погрешность и поэтому вводится новая – усеченная – функция плотности (рис. 2.30)
`f(t)=cf(t), tÎ[0,¥]
`f(t)º0, tÎ(-¥,0)
Поправочный множитель c определяют из условия нормировки усеченной плотности
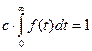
или, если 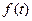 определена на отрезке (0, t0), t0>0,
определена на отрезке (0, t0), t0>0,
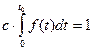
Функциональные характеристики усеченного нормального распределения имеют вид
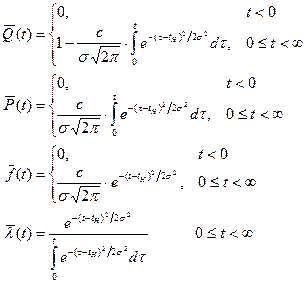 |
Числовые показатели`tН и `s2 усеченного распределения можно найти через известные tН и s2 и параметр c:
`tН=tН+с1s,
`s2= s2(1-с12-с1×tН×1/s)
где с1= (c×exp{- 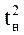 /2s2 }/
/2s2 }/ 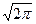 .
.
Для описания надежности серийных ТСА усеченное нормальное распределение применяется редко, ибо для технических средств автоматизации характерно большое отношение tН к s: tН/s > 2-3
