Алгоритмы нахождения наибольшего и наименьшего значения

Наибольшее или наименьше значение обычно определяется для совокупности величин (например, элементов массива). Их нахождение осуществляется в цикле путем сравнения некоторого текущего значения с наибольшим (наименьшим) из всех предшествующих. При этом, если текущее значение больше наибольшего (наименьшего) из всех предшествующих, то наибольшему (наименьшему) присваивается значение текущего. При первом прохождении цикла сравнение выполнять не надо, а следует присвоить наибольшему (наименьшему) вычисленное значение первого элемента.

Пример. Сформировать массив Zi и найти его максимальный (max) и минимальный (min) элемент и их индексы (n и k соответственно).

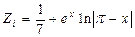для ; .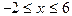

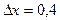Для подсчета количества элементов в массиве Z следует воспользоваться формулой:

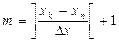, где xn=-2; xk= 6; Δx= 0,4; ]a[ - выделение целой части числа a.

Блок - схема решения этой задачи приведена на рис. 10.

В блоке 3 задается значение константы P, определяется число повторений цикла (m), оно означает и количество элементов массива Z, задается начальное значение x. Блок 4 организует цикл по переменной i, которая является индексом элементов массива Z. Блоки 5 и 6 обеспечивают формирование массива Z и вывод его элементов, а в блоке 7 организовано изменение величины x для следующего прохождения цикла. В блоке 8 присваивается значение первого элемента массива Z переменным b и c, а также запоминается индекс первого элемента (для случая, если он окажется наибольшим или наименьшим среди всех других элементов). Блок 9 организует цикл по переменной i, начиная с i=2.

В блоках 10 и 11 происходит выбор наибольшего значения из элементов массива Z и запоминание его индекса, а в блоках 12, 13 запоминаются наименьшее значение и индекс соответствующего элемента. Блок 14 выводит результаты: наибольшее и наименьшее значения и их индексы.

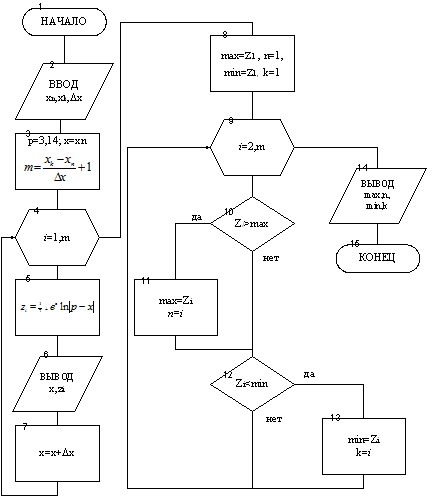
Рисунок 10 - Блок-схема алгоритма определения максимального и минимального значения