Алгоритм рисования отрезка прямой по методу брезенхема

Алгоритм Брезенхе́ма— это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками.

Отрезок проводится между двумя точками — (x0,y0) и (x1,y1), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x1 − x0 превосходит вертикальное y1 − y0, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x0 и x1, определить, какая строка y ближе всего к линии, и нарисовать точку (x,y).

Общая формула линии между двумя точками:

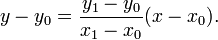
Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:

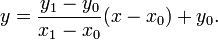
Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y0 и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона

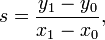
которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.

Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа:

function line(x0, x1, y0, y1)

int deltax := abs(x1 - x0)

int deltay := abs(y1 - y0)

real error := 0

real deltaerr := deltay / deltax

int y := y0

for x from x0 to x1

plot(x,y)

error := error + deltaerr

if error >= 0.5

y := y + 1

error := error - 1.0

Пусть начало отрезка имеет координаты (X₁,Y₁), а конец(X₁,X₂) . Обозначим

Dx=(X₂-X₁),dy=(Y₂-Y₁) . Не нарушая общности, будем считать, что начало отрезка совпадает с началом координат, и прямая имеет вид

Где . Считаем что начальная точка находится слева. Пусть на (i-1) -м шаге текущей точкой отрезка является P_i-1=(r,q) . Выбор следующей точки S_i или T_i зависит от знака разности (s-t). Если (s-t)<0 , то P_i=T_i=(r+1,q) и тогда

X_i+1=i+1;Y_i+1=Y_i , если же (s-t)≥0,то P_i=T_i=(r+1,q+1) и тогда X_i+1=i+1 ; Y_i+1=Y_i+1 ;

dx=(s-t)=2(rdy-qdx)+2dy –dx

Поскольку знак dx=(s-t) совпадает со знаком разности ) , то будем проверять знак выражения d_i=dx(s-t). . Так как r=X_i-1 и q=Y_i-1 ,то

d_i+1= d_i+2dy -2dx(y_i-y_i-1) .

Пусть на предыдущем шаге d_i<0 , тогда(y_i-y_i-1)=0 и d_i+1= d_i+2dy . Если же на предыдущем шаге d_i≥0 , тогда(y_i-y_i-1)=1 и d_i+1= d_i +2dx(y_i-y_i-1)

Осталось узнать как вычислить d_{i .} Так как при i=1

(x₀,y₀)=(0,0),→ d_i=2dy-dx

Далее приводится листинг процедуры на языке Паскаль, реализующей алгоритм Брезенхема.

Procedure Bresenham(x1,y1,x2,y2,Color: integer);

var

dx,dy,incr1,incr2,d,x,y,xend: integer;

begin

dx:= ABS(x2-x1);

dy:= Abs(y2-y1);

d:=2*dy-dx; {начальное значение для d}

incr1:=2*dy; {приращение для d<0}

incr2:=2*(dy-dx); {приращение для d>=0}

if x1>x2 then {начинаем с точки с меньшим знач. x}

begin

x:=x2;

y:=y2;

xend:=x1;

end

else

begin

x:=x1;

y:=y1;

xend:=x2;

end;

PutPixel(x,y,Color); {первая точка отрезка}

While x<xend do

begin

x:=x+1;

if d<0 then

d:=d+incr1 {выбираем нижнюю точку}

else

begin

y:=y+1;

d:=d+incr2; {выбираем верхнюю точку, y-возрастает}

end;

PutPixel(x,y,Color);

end;{while}

end;{procedure}

26. Общий алгоритм Брезенхема.

Алгоритм выбирает оптимальные растровые координаты для представления отрезка. Большее из приращений, либо Δx, либо Δy, выбирается в качестве единицы растра. В процессе работы одна из координат - либо x, либо y (в зависимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (на 0 или 1) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние есть ошибкой.

Алгоритм построен так, что требуется лишь знать знак этой ошибки. Следовательно, точка растра (1, 1) лучше аппроксимирует ход отрезка, чем точка (1, 0). Если угловой коэффициент меньше ½, то верно обратное. Для углового коэффициента, равного ½, нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1, 1). Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной -½. Таким образом, если угловой коэффициент отрезка больше или равен ½, то величина ошибки в следующей точке растра может быть вычислена как е = -½ + Δy/Δx.

Чтобы реализация алгоритма Брезенхема была полной, необходимо обрабатывать отрезки во всех октантах. Это легко сделать, учитывая в алгоритме номер квадранта, в котором лежит отрезок и его угловой коэффициент. Когда абсолютная величина углового коэффициента больше 1, y постоянно изменяется на единицу, а критерий ошибки Брезенхема используется для принятия решения об изменении величины x. Выбор постоянно изменяющейся (на +1 или -1) координаты зависит от квадранта

var x,y,sy,sx,dx,dy,e,z,i: Integer;
change: boolean;
begin
x:=x1; y:=y1;
dx:=abs(x2-x1); dy:=abs(y2-y1) ;
sx:=sign(x2-x1); sy:=sign(y2-y1);
e:= 2*dy-dx;
if dy<dx then change:=false
else begin
z:=dx;
dx:=dy; dy:=z;
change:=true
end;
for i:=1 to dx+dy do begin
if dy< dx then begin
if change then y:=y+sy
else x:=x+sx;
e:=e+2*dy;
end else
if change then x:=x+sx
else y:=y+sy;
e:=e-2*dx
end;
Form1.Canvas.Pixels[x,y]:=clblack; // вывод точки, для примера
end;

27. Алгоритм Брезенхема для генерації окружності

У растр потрібно розкладати як лінійні, а й інші, більш складні функції. Розкладаннюконічних перерізів, тобто кіл, еліпсів, парабол, гіпербол, було присвячено значнукількість робіт. Найбільшу увагу, зрозуміло, приділено кола. Один з найбільшефективних і простих для розуміння алгоритмів генерації окружності належитьБрезенхему. Для початку зауважимо, що необхідно згенерувати тільки одну восьмучастину кола. Решта її частини можуть бути отримані послідовними відбитками. Якщо згенерований перший октант (від 0 до 45 ° протигодинникової стрілки), то другий Октант можна отримати дзеркальним відображеннямвідносно прямої у = х, що дає в сукупності перший квадрант. Перший квадрант відбивається відносно прямої х = 0 для отримання відповідної частини кола у другому квадранті. Верхня півколо відбивається відносно прямої у = 0 для завершення побудови.

Для виведення алгоритму розглянемо першу чверть кола з центром в початкукоординат. Зауважимо, що якщо робота алгоритму починається в точці х = 0, у = R, то при генерації окружності за годинниковою стрілкою в першому квадраті у ємонотонно спадною функцією аргументів . Аналогічно, якщо вихідною точкою є у = 0, х == R, то при генерації окружності проти годинникової стрілки х будемонотонно спадною функцією аргументу у. У нашому випадку вибирається генерація за годинниковою стрілкою з початком в точці х = 0, у = R. Передбачається, що центр кола та початкова точка перебувають точно в точках растру.

Для будь-якої заданої точки на колі при генерації за годинниковою стрілкою існує тільки три можливості вибрати наступний піксел, найкращим чином наближує окружність: горизонтально вправо, по діагоналі вниз і вправо, вертикально вниз. Алгоритм вибирає піксель, для якого мінімальний квадрат відстані між одним з цих пікселів і окружністю.

28.Понятие фрактала. История фрактальной графики

В повседневной жизни часто можно наблюдать изображение (узоры), которые, казалось бы, нельзя описать математически. Пример: окна зимой замерзают, можно в итоге наблюдать картину. Подобные множества называют фрактальными. Фракталы не похожи на известные фигуры из геометрии, и строятся они по определенным алгоритмам, которые можно реализовать на компьютере. Упрощенно, фрактал - это изображение, полученное в результате некоторого преобразования, многократно примененного к исходной фигуре.
Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной процедуры превратил линию в набор несвязанных точек, которые в последствии получили название «Пыль Кантора». Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии . Для ее рисования Пеано использовал следующий алгоритм:
Он брал прямую линию и заменял её отрезками в три раза меньшей длины, чем у исходной линии. Далее он повторял это же действие с каждым из отрезков. Её уникальность в том, что она заполняет всю плоскость, т.е. для каждой точки, находящейся на плоскости можно найти точку, принадлежащую линии Пеано.
Основателем фрактальной геометрии считается Бенуа Мандельброт. Мандельброт ввел понятие «фрактал».

Фрактал - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого. Основным свойством фракталов является самоподобие, т.е. любой фрагмент фрактала в том или ином отношении воспроизводит его глобальную структуру. Фракталы делятся на геометрические, алгебраические, стохастические, системы итерируемых функций.

29. Понятие размерности и её расчет

В своей повседневной жизни мы постоянно встречаемся с размерностями. Мы прикидываем длину дороги, узнаем площадь квартиры и т.д. Это понятие вполне интуитивно ясно и, казалось бы, не требует разъяснения. Линия имеет размерность 1. Это означает, что, выбрав точку отсчета, мы можем любую точку на этой линии определить с помощью 1 числа — положительного или отрицательного. Причем это касается всех линий — окружность, квадрат, парабола и т.д.

Размерность 2 означает, что любую точку мы можем однозначно определить двумя числами. Не надо думать, что двумерный — значит плоский. Поверхность сферы тоже двумерна (ее можно определить с помощью двух значений — углов наподобие ширины и долготы).

Если смотреть с математической точки зрения, то размерность определяется следующим образом: для одномерных объектов — увеличение в два раза их линейного размера приводит к увеличению размеров (в данном случае длинны) в два раза (2^1).

Для двумерных объектов увеличение в два раза линейных размеров приводит к увеличению размера (например, площадь прямоугольника) в четыре раза (2^2).

Для 3—х мерных объектов увеличение линейных размеров в два раза приводи к увеличению объема в восемь раз (2^3) и так далее.

Таким образом, размерность D можно рассчитать исходя из зависимости увеличения «размера» объекта S от увеличения линейных размеров L. D=log(S)/log(L). Для линии D=log(2)/log(2)=1. Для плоскости D=log(4)/log(2)=2. Для объема D=log(8)/log(2)=3.

Геометрические фракталы

Именно с этим фракталов началась история развития фракталов в целом. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении геометрических фракталов руководствуются следующим алгоритмом:

1. Берется набор отрезков, на основании которых будет строится фрактал.
2. К данному набору применяют определенные правила, которые преобразуют его в какую-либо геометрическую фигуру.
3. К каждой части этой фигуры применяют тот же набор правил. С каждым шагом фигура будет становиться всё сложнее и, если провести бесконечное количество преобразований, получим геометрический фрактал.

Примеры геометрических фракталов: кривая Пеано, снежинка Коха, лист папоротника, треугольник Серпинского,

Рис. Снежинка Коха

Рис. Лист

Рис. Треугольник Серпинского

Алгебраические фракталы

Фрактал — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком

Алгебраические фракталы получили своё название за то, что их строят на основе алгебраических функцій.К алгебраическим фракталам относяться: множество Мандельброта, множество Жюлиа, басейны Ньютона, биоморфы.

-множество Мандельброта:Впервые множество Мандельброта было описано в 1905 году Пьером Фату. Фату изучал рекурсивные процессы вида

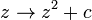
Начав с точки 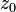на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу. Такая последовательность точек называется орбитой 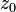при преобразовании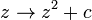

Фату нашел, что орбита 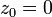при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований — своё для каждого значения . (названо мандельброта так как он первым провел необходимое количество вычислений использовав компьютер).

-множество Жюлиа: мно́жество Жюлиа́ 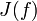рационального отображения 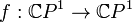— множество точек, динамика в окрестности которых в определённом смысле неустойчива по отношению к малым возмущениям начального положения. В случае, если f — полином, рассматривают также заполненное множество Жюлиа — множество точек, не стремящихся к бесконечности. Обычное множество Жюлиа при этом является его границей.

-бассейны Ньютона:Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона накомплексной плоскости (для функции действительной переменной метод Ньютона часто называют методом касательных, который, в данном случае, обобщается для комплексной плоскости).

Применим метод Ньютона для нахождения нуля функции комплексного переменного, используя процедуру:

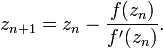
Выбор начального приближения 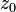представляет особый интерес. Т.к. функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям.

-биоморфы: сокращенная форма множества Жюлиа, вычисляеться по формуле z=z³+c. Название получила из-за схожести с одноклеточными организмами.

Стохастические фракталы

Типичным представителем данного вида фракталов является так называемая плазма.

Для её построения берут прямоугольник и для каждого его угла определяют цвет. Далее находят центральную точку прямоугольника и раскрашивают её в цвет, равный среднеарифметическому цветов по углам прямоугольника + некоторое случайное число. Чем больше это случайно число - тем более рваным будет рисунок.

Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:

траектория броуновского движения на плоскости и в пространстве;

граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельброта о том, что её размерность равна 4/3.

эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например, в модели Изинга и перколяции.

различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике.

Фрактальная монотипия, или стохатипия — направления в изобразительном искусстве, заключающиеся в получении изображения случайного фрактала.