Построение графиков в логарифмическом и полулогарифмическом масштабах.

Если для одиночного графика диапазоны изменения переменных вдоль одной или обеих осей координат слишком велики, то можно воспользоваться функциями построения графиков в логарифмическом и полулогарифмических масштабах. Для этого предназначены функции semilogx (логарифмический масштаб по оси 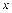), semilogy (логарифмический масштаб по оси 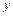) и loglog (логарифмический масштаб по обеим осям). Синтаксис указанных функций аналогичен синтаксису функции plot: они принимают аргументы, заданные в виде пары векторов значений абсцисс и ординат.

Построим в качестве примера график функции на промежутке в логарифмическом масштабе по оси .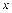

Будем иметь (рис. 2.9.6):

>> x=0.1:0.001:1000;

>> y=3*cos(log(2*x));

>> semilogx(x,y)

Рис. 2.9.6. График функции в логарифмическом масштабе по оси .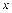

Построение графиков в полярных координатах.

Для построения графика функции в полярной системе координат используется команда polar, например (рис. 2.9.7):

>> phi=0:0.001:2*pi;

>> r=sin(5*phi);

>> polar(phi,r);

Оформление графиков и графических окон

Функции построения графиков, рассмотренные в предыдущем параграфе осуществляли автоматическое оформление графиков. Разумеется у системы MATLAB имеются дополнительные возможности, связанные с управлением внешним видом графика – заданием цвета и стиля линий, а также размещение различных надписей в пределах графического окна.

Рис. 2.9.7. График функции в полярной системе координат.

Рис. 2.10.1. Пример маркировки точек кривой посредством окружностей.

Выбор свойств линий.

Так, например, команды (рис. 2.10.1)

>> x=0:0.1:2*pi;

>> y=cos(x);

>> plot(x, y, 'k-', x, y, 'ko')

позволяют придать графику вид черной сплошной линии, на которой в дискретных точках, расстояние между которыми равно 0.1, проставляются черные окружности. Здесь функция plot дважды строит график одной и той же функции, но в двух разных стилях. Первый из этих стилей отмечен как “k-”, что обозначает проведение линии черным цветом (буква k), а штрих означает проведение сплошной линии. Второй стиль, помеченный как “ko”, обозначает проведение тем же черным цветом (буква k) окружностей (буква o) на месте вычисляемых точек.

В общем случае команда

plot(x1,y1,s1,x2,y2,s2,...)

позволяет определить в одном графическом окне изображения нескольких функций y1(x1),y2(x2),... используя стили s1,s2,....

Заметим, что стили s1,s2,... задаются в виде набора трех символьных маркеров (стилевой строки), один из которых задает тип линии, второй – цвет линии, а третий – тип маркера, используемого для пометки представляемых точек (таблица 2.10.1). При отсутствии указания типов маркеров используются значения, установленные по умолчанию. Отметим, что порядок, в которым указываются маркеры, задающие тип линии, цвет линии и тип точки несущественен. Если в стилевой строке задан тип маркера, но не указан тип линии, то представляемые точки маркером метятся, но не соединяются друг с другом отрезками прямых.

Более мощным способом построения графиков функций является метод дескрипторов, который относится к низкоуровневой графике MATLAB. Метод дискрипторов позволяет напрямую обратиться к базовым графическим объектам и задать его свойства. Детальное знакомство со свойствами графических объектов MATLAB выходит за рамки книги.

В этой связи приведем ниже некоторый пример, иллюстрирующий основные приемы работы с дискрипторной графикой и позволяющий продемонстрировать суть данного метода (рис. 2.10.2).

>> x=0:0.001:2*pi;

>> y=cos(x);

>> hplot=plot(x,y);

>> set(hplot,'LineWidth',8);

В данном случае команда plot через опорные точки проводит отрезки прямых линий с координатами x,y. Прямые линии в системе MATLAB представляют собой объекты типа line. Эти объекты имеют очень большое количество свойств и характеристик, которые можно менять. Доступ к этим объектам осуществляется посредством их дескрипторов.

Командой hplot=plot(x,y) создается графический объект и переменной hplot присваивается значение дескриптора графического объекта типа line, использованного для построения графика функции .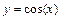

Таблица 2.10.1. Параметры для управления цветом и видом графиков.

Параметр	Обозначение (управляющий символ)
Тип линии
сплошная (по умолчанию)	-
пунктирная	:
штриховая	--
штрих-пунктирная	-.
Цвет линии
красный (от англ. red)	r
желтый (от англ. yellow)	y
зеленый (от англ. green)	g
синий (от англ. blue)	b
голубой /циановый/ (от англ. cyan)	c
розовый /малиновый/ (от англ. magenta)	m
черный (от англ. black)	k
белый (от англ. white)	w
Тип маркера
точка (жирная точка)	.
кружок	о
крестик (косоугольный крестик)	x
плюс (прямоугольный крестик)	+
звездочка (восьмиконечная снежинка)	*
квадратик	s
ромбик	d
отсутствие маркера	none
треугольник вершиной вниз	v
треугольник вершиной вверх	^
треугольник вершиной влево	<
треугольник вершиной вправо	>
пятиконечная звезда	p
шестиконечная звезда	h

Затем данный дескриптор передается в качестве параметра функции set для опознания конкретного графического объекта и задания значений соответствующих свойств объекта.

В рассматриваемом примере было установлено значение свойства 'LineWidth' (толщина линии) равным 7 (по умолчанию 0.5). График, полученный в результате изменения толщины линии, представлен на рис. 2.10.2.

Текущее значение любого параметра (атрибута; характеристики) графического объекта возвращается функцией get. Так, например, если после получения показанного на рис. 2.10.1 графика выполнить команду

>> width=get(hplot, 'LineWidth')

width =

Рис. 2.10.2. График функции 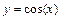на интервале 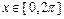(толщина кривой – 7 пикселей).

то для переменной width будет присвоено значение свойства 'LineWidth' равное 7.

Для получения списка всех свойств графического объекта следует обратиться к функции get, указав ей в качестве единственного параметра дескриптор объекта. Так, например, для дескриптора hplot объекта типа line можно найти весь список его свойств:

>> get(hplot);

DisplayName: ''

Annotation: [1x1 hg.Annotation]

Color: [0 0 1]

LineStyle: '-'

LineWidth: 7

Marker: 'none'

MarkerSize: 6

MarkerEdgeColor: 'auto'

MarkerFaceColor: 'none'

XData: [1x6284 double]

YData: [1x6284 double]

ZData: [1x0 double]

BeingDeleted: 'off'

ButtonDownFcn: []

Children: [0x1 double]

Clipping: 'on'

CreateFcn: []

DeleteFcn: []

BusyAction: 'queue'

HandleVisibility: 'on'

HitTest: 'on'

Interruptible: 'on'

Selected: 'off'

SelectionHighlight: 'on'

Tag: ''

Type: 'line'

UIContextMenu: []

UserData: []

Visible: 'on'

Parent: 173.0011

XDataMode: 'manual'

XDataSource: ''

YDataSource: ''

ZDataSource: ''

Среди свойств графического объекта с дескриптором hplot имеются интуитивно понятные. В частности, помимо уже рассмотренного свойства 'LineWidth', свойство 'Color' отвечает за цвет линии в RGB-кодировке (красный, зеленый, синий) и так как значение поля равно [0 0 1], то цвет линии синий, а свойство 'MarkerSize' определяет размер маркера точек графика (в данном случае равного 6). Установленные значения полей указываются в списке свойств справа от знака равно, при этом свойства, значения которых не установлены, отмечены пустым полем или знаком [].