Структурная схема и математическая модель типичной стеганосистемы
В общем случае стеганосистема может быть рассмотрена как система связи [5]. Обобщенная структурная схема стеганосистемы изображена на рис. 2.3
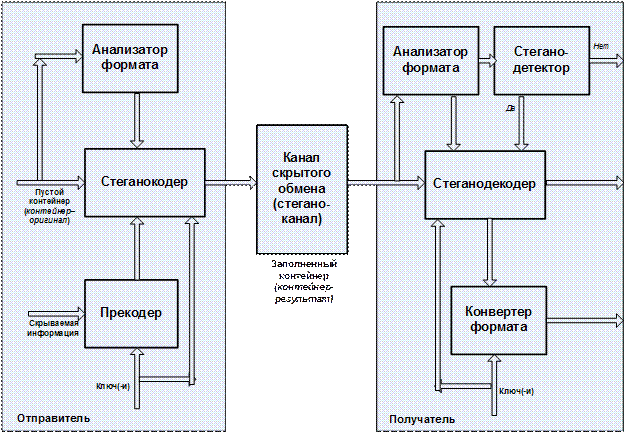
Рис. 2.3. Структурная схем стеганосистемы как системы связи
Основными стеганографическими понятиями являются сообщение и контейнер. Сообщение 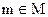 — это секретная информация, наличие которой необходимо скрыть,
— это секретная информация, наличие которой необходимо скрыть, 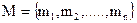 — множество всех сообщений.
— множество всех сообщений.
Контейнером 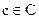 называется несекретная информация, которую можно использовать для скрытия сообщения,
называется несекретная информация, которую можно использовать для скрытия сообщения, 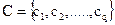 — множество всех контейнеров, причем q >> n. В качестве сообщения и контейнера могут выступать как обычный текст, так и файлы мультимедийного формата.
— множество всех контейнеров, причем q >> n. В качестве сообщения и контейнера могут выступать как обычный текст, так и файлы мультимедийного формата.
Пустой контейнер (или так называемый контейнер-оригинал) — это контейнер с, который не содержит скрытой информации. Заполненный контейнер (контейнер-результат) — контейнер с, который содержит скрытую информацию 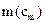 . Одно из требований, которое при это ставится: контейнер-результат не должен быть визуально отличим от контейнера-оригинала. Выделяют два основных типа контейнера: потоковый и фиксированный.
. Одно из требований, которое при это ставится: контейнер-результат не должен быть визуально отличим от контейнера-оригинала. Выделяют два основных типа контейнера: потоковый и фиксированный.
Потоковый контейнер представляет собой последовательность битов, которая непрерывно изменяется. Сообщение встраивается в него в реальном масштабе времени, поэтому в кодере заранее неизвестно, хватит ли размеров контейнера для передачи всего сообщения. В один контейнер большого размера может быть встроено несколько сообщений. Интервалы между встроенными битами определяются генератором ПСП с равномерным распределением интервалов между отсчетами.
Основная проблема заключается в выполнении синхронизации, определении начала и конца последовательности. Если в данных контейнера существуют биты синхронизации, заголовки пакетов и т д., то скрытая информация может следовать сразу же после них. Сложность организации 'синхронизации является преимуществом с точки зрения обеспечения скрытости передачи. К сожалению, на сегодняшний день практически отсутствуют работы, посвященные разработке стеганосистем с потоковым контейнером
В качестве примера перспективной реализации потокового контейнера можно привести стеганоприставку к обычному телефону. При этом под прикрытием заурядного, несущественного телефонного разговора можно передавать другой разговор, данные и т.д. Не зная секретного ключа, нельзя не только узнать о содержании скрытой передачи, но и о самом факте ее существования.
В фиксированном контейнере размеры и характеристики последнего заранее известны. Это позволяет выполнять вложение данных оптимальным (в определенном смысле) образом. Далее будут рассматриваться преимущественно фиксированные контейнеры (в дальнейшем — просто "контейнеры").
Контейнер может быть избранным, случайным или навязанным. Избранный контейнер зависит от встроенного сообщения, а в предельном случае является его функцией Такой тип контейнера больше характерен именно для стеганографии Навязанный контейнер появляется, когда лицо, которое предоставляет контейнер, подозревает о возможной скрытой переписке и желает предотвратить ее. На практике же чаще всего имеют дело со случайным контейнером [5].
Скрытие информации, которая преимущественно имеет большой объем, выдвигает существенные требования к контейнеру, размер которого должен по меньшей мере в несколько раз превышать размер встраиваемых данных. Понятно, что для увеличения скрытости указанное соотношение должно быть как можно большим.
Перед тем как выполнить вложение сообщения в контейнер, его необходимо преобразовать в определенный удобный для упаковки вид. Кроме того, перед упаковкой в контейнер, для повышения защищенности секретной информации последнюю можно зашифровать достаточно устойчивым криптографическим кодом [14].
Во многих случаях также желательна устойчивость полученного стеганосообщения к искажениям (в том числе и злоумышленным) [5].
В процессе передачи звук, изображение или какая-либо другая информация, используемая в качестве контейнера, может подвергаться разным трансформациям (в том числе с использованием: алгоритмов с потерей данных): изменение объема, преобразование в другой формат и т.п., — поэтому для сохранения целостности встроенного сообщения может понадобиться использование кода с исправлением ошибок (помехоустойчивое кодирование).
Начальную обработку скрываемой информации выполняет изображенный на рис. 2.3 прекодер. В качестве одной из важнейших предварительных обработок сообщения (а также и контейнера) можно назвать вычисление его обобщенного преобразования Фурье. Это позволяет осуществить встраивание данных в спектральной области, что значительно повышает их устойчивость к искажениям
Следует отметить, что для увеличения секретности встраивания, предварительная обработка довольно часто выполняется с использованием ключа.
Упаковка сообщения в контейнер (с учетом формата данных, представляющих контейнер) выполняется с помощью стеганокодера. Вложение происходит, например, путем модификации наименьших значащих битов контейнера. Вообще, именно алгоритм (стратегия) внесения элементов сообщения в контейнер определяет методы стеганографии, которые в свою очередь делятся на определенные группы, например, в зависимости от того, файл какого формата был выбран в качестве контейнера.
В большинстве стеганосистем для упаковки и извлечения сообщений используется ключ, который предопределяет секретный алгоритм, определяющий порядок внесения сообщения в контейнер. По аналогии с криптографией, тип ключа обуславливает существование двух типов стеганосистем:
• с секретным ключом — используется, один ключ, который определяется до начала обмена стеганограммой или передается защищенным каналом;
• с открытым ключом — для упаковки и распаковки сообщения используются разные ключи, которые отличаются таким образом, что с помощью вычислений невозможно получить один ключ из другого, поэтому один из ключей (открытый) может свободно передаваться по незащищенному каналу.
В качестве секретного алгоритма может быть использован генератор псевдослучайной последовательности (ПСП) битов. Качественный генератор ПСП, ориентированный на использование в системах защиты информации, должен соответствовать определенным требованиям [42]. Перечислим некоторые из них.
• Криптографическая стойкость — отсутствие у нарушителя возможности предусмотреть следующий бит на основании известных ему предыдущих с вероятностью, отличной от 1/2. На практике криптографическая стойкость оценивается статистическими методами. Национальным Институтом Стандартов и Технологий США (НИСТ) разработано Руководство по проведению статистических испытаний генераторов ПСП, ориентированных на использование в задачах криптографической зашиты информации [43]).
• Хорошие статистические свойства — ПСП по своим статистическим свойствам не должна существенно отличаться от истинно случайной последовательности.
• Большой период формированной последовательности.
• Эффективная аппаратно-программная реализация.
Статистически (криптографически) безопасный генератор ПСП должен соответствовать следующим требованиям:
• ни один статистический тест не определяет в ПСП никаких закономерностей, иными словами, не отличает эту последовательность от истинно случайной;
• при инициализации случайными значениями генератор порождает статистически независимые псевдослучайные последовательности.
В качестве основы генератора может использоваться, например, линейный рекуррентный регистр. Тогда адресатам для обеспечения связи должно сообщаться начальное заполнение этого регистра. Числа, порождаемые генератором ПСП, могут определять позиции модифицированных отсчетов в случае фиксированного контейнера или интервалы между ними в случае потокового контейнера.
Следует отметить, что метод случайного выбора величины интервала между встроенными битами не является достаточно эффективным по двум причинам. Во-первых, скрытые данные должны быть распределены по всему контейнеру, поэтому равномерное распределение длины интервалов (от наименьшего к наибольшему) может быть достигнуто только приблизительно, поскольку должна существовать уверенность в том, что все сообщение встроено (то есть, поместилось в контейнер). Во-вторых, длина интервалов между отсчетами шума (во многих моделях сигнал-контейнер рассматривается как аддитивный шум [44]) распределена не по равномерному, а по экспоненциальному закону. Генератор ПСП с экспоненциальным распределением интервалов сложен в реализации.
Скрываемая информация заносится в соответствии с ключом в те биты, модификация которых не приводит к существенным искажениям контейнера. Эти биты образуют так называемый стеганопутъ. Под "существенным" подразумевается искажение, которое приводит к росту вероятности выявления факта наличия скрытого сообщения после проведения стеганоанализа.
Стеганографический канал — канал передачи контейнера-результата (вообще, существование канала как, собственно говоря, и, получателя — наиболее обобщенный случай, поскольку заполненный контейнер может, например, храниться у "отправителя", который поставил перед собой цель ограничить неавторизованный доступ к определенной информации. В данном случае отправитель выступает в роли получателя). Во время пребывания в стеганографическом канале контейнер, содержащий скрытое сообщении, может подвергаться умышленным атакам или случайным помехам, детальное описание которых представлено в главе 3.
В стеганодетекторе определяется наличие в контейнере (возможно уже измененном) скрытых данных. Это изменение может быть обусловлено влиянием ошибок в канале связи, операций обработки сигнала, намеренных атак нарушителей. Как уже отмечалось выше, во многих моделях стеганосистем сигнал-контейнер рассматривается как аддитивный шум. Тогда задача выявления и выделения стеганосообщения является классической для теории связи [70]. Но такой подход не учитывает двух факторов: неслучайного характера контейнера и требований по сохранению его качеств. Эти моменты не встречаются в известной теории обнаружения и выделения сигналов на фоне аддитивного шума. Очевидно, что их учет позволит построить более эффективные стеганосистемы [5].
Различают стеганодетекторы, предназначенные только для обнаружения факта наличия встроенного сообщения, к устройства, предназначенные для выделения этого сообщения из контейнера, — стеганодекодеры.
Итак, в стеганосистеме происходит объединение двух типов информации таким образом, чтобы они по-разному воспринимались принципиально разными детекторами. В качестве одного из детекторов выступает система выделения скрытого сообщения, в качестве другого — человек.
Алгоритм встраивания сообщения в простейшем случае состоит из двух основных этапов:
1. Встраивание в стеганокодере секретного сообщения в контейнер-оригинал.
2. Обнаружение (выделение) в стеганодетекторе (декодере) скрытого зашифрованного сообщения из контейнера-результата.
Исходя из этого, рассмотрим математическую модель стеганосистемы. Процесс тривиального стеганографического преобразования описывается зависимостями:
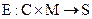 (2.1)
(2.1)
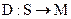 (2.1)
(2.1)
где 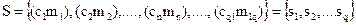 — множество контейнеров-результатов (стеганограмм).
— множество контейнеров-результатов (стеганограмм).
Зависимость (2.1) описывает процесс скрытия информации, зависимость (2.2)— извлечение скрытой информации. Необходимым условием при этом является отсутствие "пересечения" [3], то есть, если 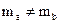 , причем
, причем 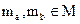 , а
, а 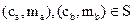 , то
, то 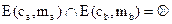 .
.
Кроме того, необходимо, чтобы мощность множества 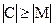 .При этом оба адресата (отправитель и получатель) должны знать алгоритм прямого (Е) и обратного (D) стеганографического преобразования.
.При этом оба адресата (отправитель и получатель) должны знать алгоритм прямого (Е) и обратного (D) стеганографического преобразования.
Итак, в общем случае стеганосистема — это совокупность 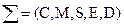 контейнеров (оригиналов и результатов), сообщений и преобразования, которые их связывают.
контейнеров (оригиналов и результатов), сообщений и преобразования, которые их связывают.
Для большинства стеганосистем множество контейнеров С выбирается таким образом, чтобы в результате стеганографического преобразования (2.1) заполненный контейнер и контейнер-оригинал были подобны, что формально может быть оценено с помощью функции подобия [3].
Определение 2.1
Пусть С — непустое множество, тогда функция 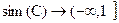 является функцией подобия на множестве С, если для каких-либо
является функцией подобия на множестве С, если для каких-либо 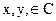 справедливо, что
справедливо, что 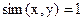 в случае
в случае 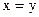 и
и 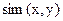 <1 при
<1 при 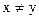 .
.
Стеганосистема может считаться надежной, если 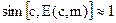 для всех
для всех 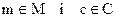 , причем в качестве контейнера с должен избираться такой, который ранее не использовался. Кроме того, неавторизованное лицо не должно иметь доступ к набору контейнеров, используемых для секретной связи.
, причем в качестве контейнера с должен избираться такой, который ранее не использовался. Кроме того, неавторизованное лицо не должно иметь доступ к набору контейнеров, используемых для секретной связи.
Выбор определенного контейнера с из набора возможных контейнеров С может осуществляться произвольно (так называемый суррогатный метод выбора контейнера) или путем избрания наиболее пригодного, который менее других изменится во время стеганопреобразования (селективный метод). В последнем случае контейнер избирается в соответствии с правилом:
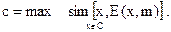 (2.3)
(2.3)
Также следует отметить, что функции прямого (Е) и обратного (D) стеганографического преобразовання в общем случае могут быть произвольными (но, конечно, соответствующими одна другой), однако на практике требования к устойчивости скрытой информации накладывают на указанные функции определенные ограничения.
Так, в подавляющем большинстве случаев, 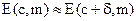 или
или 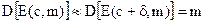 , то есть, незначительно модифицированный контейнер (на величину 5) не должен приводить к изменению скрытой в нем информации [5].
, то есть, незначительно модифицированный контейнер (на величину 5) не должен приводить к изменению скрытой в нем информации [5].
