Перевод из двоичной системы счисления в восьмеричную и обратно

Аналогично переводу из двоичной системы счисления в шестнадцатеричную. Главным отличием является то, что основанием будет 8, а не 16, и деление числа производится не тетрадами, а группами по три числа.

1. Выполнить перевод числа 10011₂ в восьмеричную систему счисления

10|011₂=010|011₂

010₂=2₈

010011₂=23₈

011₂=3₈

1. Выполнить перевод числа 10110010₂ в восьмеричную систему счисления

10|110|010₂=010|110|010₂

010₂=2₈

110₂=6₈

010₂=2₈

10110010₂=262₈

1. Выполнить перевод числа 0,0010101₂ в восьмеричную систему счисления

001|010|1₂=001|010|100₂

001₂=1₈

010₂=2₈

100₂=4₈

0,0010101₂=0,124₈

Перевод из восьмеричную системы счисления в двоичную:

1. Выполнить перевод числа 13₈ в двоичную систему счисления

1₈=1₂=001₂;

3₈=11₂=011₂.

13₈ = 001|011₂.

После удаления незначащих нулей имеем 13₈=1011₂

1. Выполнить перевод числа 137₈ в двоичную систему счисления

1₈=001₂

3₈=011₂

7₈=111₂

001|011|111₂=1|011|111₂

13₈=1011111₂

1. Выполнить перевод числа 0,74₈ в двоичную систему счисления

7₈=111₂

0,74₈=0,111100₂

4₈=100₂.

Таблица 2. Основные методы

10→2		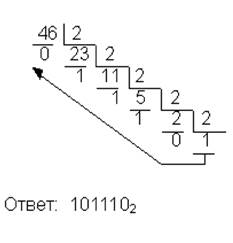2→10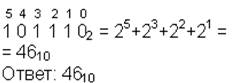
2→16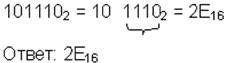
2→8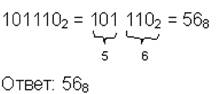
10→8		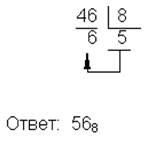8→2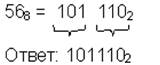
8→10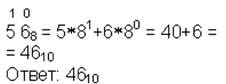
8→16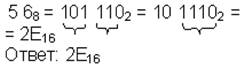
10→16		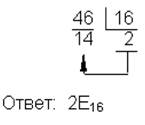16→2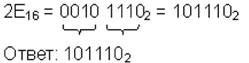
16→8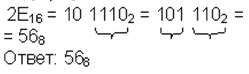
16→10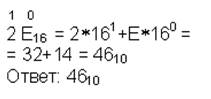

Арифметические операции в позиционных системах счисления

Сложение

Правила сложения в любой позиционной системе счисления аналогичны правилам сложения в десятичной системе счисления. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

1. Сложим числа 15 и 6 в различных системах счисления.

Десятичная 15₁₀+6₁₀ Двоичная 1111₂+110₂ Восьмеричная 17₈+6₈

Шестнадцатеричная: F₁₆+6₁₆

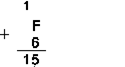
Проверка. Преобразуем полученные суммы к десятичному виду:
10101₂ = 2⁴ + 2² + 2⁰ = 16+4+1=21,
25₈ = 2∙8¹ + 5∙8⁰ = 16 + 5 = 21,
15₁₆ = 1∙16₁ + 5∙16₀ = 16+5 = 21.

Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆

2. Сложим числа 15, 7 и 3.

Десятичная 15₁₀+7₁₀ +3₁₀ Двоичная 1111₂+111₂+11₂ Восьмеричная 17₈+7₈+3₈

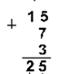
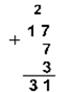
Шестнадцатеричная: F₁₆+7₁₆+3₁₆

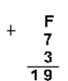
Проверка:
11001₂ = 2⁴ + 2³ + 2⁰ = 16+8+1=25,
31₈ = 3*8¹ + 1*8⁰ = 24 + 1 = 25,
19₁₆ = 1*16¹ + 9*16⁰ = 16+9 = 25.

Ответ: 15+7+3 = 25₁₀ = 11001₂ = 31₈ = 19₁₆.

Вычитание

1. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Двоичная 10₂–1₂ Восьмеричная 10₈–1₈ Шестнадцатеричная 10₁₆–1₁₆

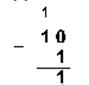
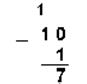
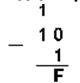
2. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

Двоичная 100₂–1₂ Восьмеричная 100₈–1₈ Шестнадцатеричная 100₁₆–1₁₆

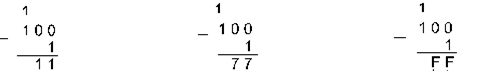
3. Вычтем число 59,75 из числа 201,25 в различных системах счисления

Десятичная 201,25₁₀ – 59,75₁₀ Двоичная 11001001,01₂–111011,11₂

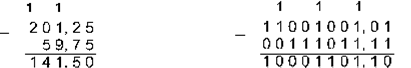
Восьмеричная 311,2₈–73,6₈ Шестнадцатеричная С9,4₁₆–3B,C₁₆

Ответ: 201,25₁₀ – 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.

Умножение и деление в двоичной системе

1. Умножение в двоичной системе производится по тому же принципу что и в десятичной системе счисления, при этом используется таблица двоичного умножения:

0 ∙ 0 = 0

0 ∙ 1 = 0

1 ∙ 0 = 0

1 ∙ 1 = 1

Умножим число 10101 на 1001 и число 1101 на 11:

2. Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля.

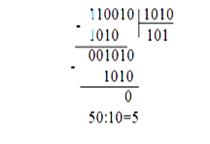
Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования

MAC адрес.

MAC адрес - это уникальный, серийный номер, назначаемый каждому сетевому устройству, для идентификации его в сети. Этот адрес является уникальным для каждого устройства и устанавливается при его производстве.

MAC адреса обычно записываются шестнадцатеричным числом в виде 12:34:56:78:90:AB

Узнать MAC адрес компьютера и перевести его в десятичную систему счисления.

1) Запустите окно командной строки (ПУСК-Выполнить-cmd) и выполните команду:

IPCONFIG /ALL

2) Получите таблицу, в которой, в частности, присутствует Physical address (физический адрес) - это и есть MAC-адрес.

3) Например: 00-FF-0E-BA-34-B1

4) Перевод:

00₁₆=0₁₀

FF₁₆=F∙16¹+F∙16⁰= 15∙16¹+15∙160=25510

0E₁₆=0∙16¹+E∙16⁰=0∙16¹+14∙16⁰=14₁₀

BA₁₆=B∙16+A∙16⁰= 11∙16+10∙16⁰ =176₁₀+10₁₀=186₁₀

34₁₆=3∙16+4∙16⁰=52₁₀

B1₁₆= B∙16+1∙16⁰=11∙16+1∙16⁰=171₁₀

5) MAC-адрес в десятичной системе: 255-014-186-052-171

Бит и байт

Размер:	Скорость:
бит (англ. bit)	Бит – двоичный разряд в двоичной системе счисления)	бит в секунду	бит в секунду — бит/c (bps) англ. bits per second килобит в секунду — Кбит/c (Kbps) мегабит в секунду — Мбит/c (Mbps) гигабит в секунду — Гбит/c (Gbps)
байт (англ. byte)	1 Байт = 8 бит	байт в секунду	байт в секунду — Б/c (Bps) англ. bytes per second килобайт в секунду — Кб/с (KBps) мегабайт в секунду — Мб/c (MBps) гигабайт в секунду — Гб/c (GBps)

кило = 1.000 (103)	1 Кбайт = 1 024 байт	1 Кбит = 1 024 бита
мега = 1.000.000 (106)	1 Мбайт = 1 048 576 байт (1 0242)	1 Мбит = 1 048 576 бит
гига = 1.000.000.000 (109)	1 Гбайт=1 073 741 824 байт (10243)	1 Гбит = 1 073 741 824 бита

1 Кбайт = 1 024 байт = 8 192 бит

1 Мбайт = 1 024 Кбайт = 1 048 576 байт = 8 388 608 бит

1 Гбайт = 1 024Мбайт = 1 048 576 Кбайт = 1 073 741 824 байт = 8 589 934 592 бит

1 Кбит = 1 024 бит = 128 байт = 0,125 Кбайт

1 Мбит = 1 024 Кбит=1 048 576 бит = 131 072 байт = 128 Кбайт = 0,125 Мбайт

1 Гбит =1 024 Мбит =1 048 576 Кбит = 1 073 741 824 бит = 134 217 728 байт = 131072 Кбайт = 128 Мбайт = 0,125 Гбайт

Правила:

Что бы перевести байты в биты надо умножить на 8

Что бы перевести биты в байты надо делить на 8

Что бы перевести в большую степень байт >> килобайт >> мегабайт >> гигабайт надо делить на 1 024

Что бы перевести в меньшую степень гигабайт >> мегабайт >> килобайт >> байт надо умножать на 1 024

1. Провайдер заявляет, что скорость соединения с интернет 6 мегабит/с, а менеджер закачки показывает 730 Кб/с (KBps). Менеджеры закачки показывают только полезную скорость, т.е. ту с которой он закачивает на Ваш компьютер файлы, но есть ещё и техническая информация, которая занимает около 10%.

1) Добавим к скорости 10% от 730 Кб/с

730+730∙10/100=803 Кб/с

2) Перевод Кб/с в Кбит/с

803 ∙ 8 = 6424 Кбит/c

3) Перевод Кбит/c в Мбит/c

6424 : 1024 = 6,3 Мбит/c

2. Время скачивания:

Сколько времени понадобится на передачу файла, размером 7 Гбайт, на скорости 730 Кб/с?

1) перевод 7 Гбайт в Кбайт

1 Гбайт = 1 073 741 824 Байт

7 Гбайт = 7 516 192 768 Байт=7 340 032 Кбайт

2) время = размер/скорость

7 340 032 Кбайт/730 Кб/с=10054 с

3) перевод сек в часы

10054 с = 168 минут = 2 часа 48 минут.

Упражнения

1. Перевести целые числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную и сделать проверку.

1) 156	2) 98	3) 171	4) 153	5) 175
6) 237	7) 138	8) 241	9) 161	10) 178
11) 195	12) 103	13) 158	14) 216	15) 60
16) 31	17) 13	18) 29	19) 33	20) 49

1) 156₁₀ = 1001110₂ = 234₈ = 9C₁₆ 11) 195₁₀ = 11000011₂ = 303₈ = C3₁₆

2) 98₁₀ = 1100010₂ = 142₈ = 62₁₆ 12) 103₁₀ = 1100111₂ = 147₈ = 67₁₆

3) 171₁₀ = 10101011₂ = 253₈ = AB₁₆ 13) 158₁₀ = 10011110₂ = 236₈ = 9E₁₆

4) 153₁₀ = 10011001₂ = 231₈ = 99₁₆ 14) 216₁₀ = 11011000₂ = 330₈ = D8₁₆

5) 175₁₀ = 10101111₂ = 257₈ = AF₁₆ 15) 60₁₀ = 111100₂ = 74₈ = 3C₁₆

6) 237₁₀ = 11101101₂ = 355₈ = ED₁₆ 16) 31₁₀ = 11111₂ = 37₈ = 1F₁₆

7) 138₁₀ = 10001010₂ = 212₈ = 8A₁₆ 17) 13₁₀ = 1101₂ = 15₈ = D₁₆

8) 241₁₀ = 11110001₂ = 361₈ = F1₁₆ 18) 29₁₀ = 11101₂ = 35₈ = 1D₁₆

9) 161₁₀ = 10100001₂ = 241₈ = A1₁₆ 19) 33₁₀ = 100001₂ = 33₈ = 21₁₆

10) 178₁₀ = 10110010₂ = 262₈ = B2₁₆ 20) 49₁₀ = 110001₂ = 61₈ = 31₁₆

2. Перевести числа из десятичной системы в двоичную (с точностью до 4 знаков), восьмеричную (с точностью до 3 знаков) и шестнадцатеричную (с точностью до 2 знаков) и сделать проверку.

1) 5,43	2) 17,45	3) 9,89	4) 2,78	5) 4,19
6) 3,14	7) 12,13	8) 4,71	9) 2,95	10) 0,78
11) 9,51	12) 18,23	13) 2,18	14) 8,17	15) 10,46
16) 2,67	17) 9,43	18) 2,15	19) 9,27	20) 7,13

1) 5,43₁₀ = 101,0110₂ = 5,334₈ = 5,6E₁₆ 11) 9,51₁₀ = 1001,1000₂ = 11,405₈ = 9,82₁₆

2) 17,45₁₀ = 10001,0111₂ = 21,346₈ = 11,73₁₆ 12) 18,23₁₀ = 10010,0011₂ = 22,165₈ = 12,3A₁₆

3) 9,89₁₀ = 1001,1110₂ = 11,707₈ = 9,E3₁₆ 13) 2,18₁₀ = 10,0010₂ = 2,134₈ = 2,2E₁₆

4) 2,78₁₀ = 10,1100₂ = 2,617₈ = 2,C7₁₆ 14) 8,17₁₀ = 1000,1011₂ = 10,546₈ = 8,B3₁₆

5) 4,19₁₀ = 100,0011₂ = 4,141₈ = 4,30₁₆ 15) 10,46₁₀ = 1010,0111₂ = 12,353₈ = A,75₁₆

6) 3,14₁₀ = 11,0010₂ = 3,107₈ = 3,23₁₆ 16) 2,67₁₀ = 10,1010₂ = 2,527₈ = 2,AB₁₆

7) 12,13₁₀ = 1100,0010₂ = 14,102₈ = C,21₁₆ 17) 9,43₁₀ = 1001,0110₂ = 11,334₈ = 9,6E₁₆

8) 4,71₁₀ = 100,1011₂ = 4,553₈ = 4,B5₁₆ 18) 2,15₁₀ = 10,0010₂ = 2,114₈ = 2,26₁₆

9) 2,95₁₀ = 10,1111₂ = 2,746₈ = 2,F3₁₆ 19) 9,27₁₀ = 1001,0100₂ = 11,212₈ = 9,45₁₆

10) 0,78₁₀ = 0,1100₂ = 0,617₈ = 0,C7₁₆ 20) 7,13₁₀ = 111,0010₂ = 7,102₈ = 7,21₁₆

3. Переведите числа в десятичную, восьмеричную и шестнадцатеричную системы, а затем проверьте результаты, выполнив обратные переводы:

1) 10110112	2) 101101112	3) 0111000012	4) 0,10001102	5) 0,101010112
6) 0,111100112	7) 0,001001012	8) 1100111112	9) 11110110112	10) 1101101102
11) 10010000102	12) 0,111010112	13) 0,100110112	14) 111111102	15) 1110001002
16) 100000002	17) 0,101010112	18) 0,111001012	19) 111110102	20) 1010010102

1) 1011011₂ = 91₁₀ = 133₈ = 5B₁₆ 11) 1001000010₂ = 578₁₀ = 1102₈ = 242₁₆

2) 10110111₂ = 183₁₀ = 267₈ = B7₁₆ 12) 0,11101011₂ = 0,91796875₁₀ = 0,726₈ = 0,EB₁₆

3) 011100001₂ = 225₁₀ = 341₈ = E1₁₆ 13) 0,10011011₂ = 0,60546875₁₀ = 0,466₈ = 0,9B₁₆

4) 0,1000110₂ = 0,54₁₀ = 0,43₈ = 0,8C₁₆ 14) 11111110₂ = 254₁₀ = 376₈ = FE₁₆

5) 0,10101011₂ = 0,66796875₁₀ = 0,526₈ = 0,AB₁₆ 15) 111000100₂ = 452₁₀ = 704₈ = 1C4₁₆

6) 0,11110011₂ = 0,94921875₁₀ = 0,746₈ = 0,F3₁₆ 16) 10000000₂ = 128₁₀ = 200₈ = 80₁₆

7) 0,00100101₂ = 0,14453125₁₀ = 0,112₈ = 0,25₁₆ 17) 0,10101011₂ = 0,66796875₁₀ = 0,526₈ = 0,AB₁₆

8) 110011111₂ = 415₁₀ = 637₈ = 19F₁₆ 18) 0,11100101₂ = 0,89453125₁₀ = 0,712₈ = 0,E5₁₆

9) 1111011011₂ = 987₁₀ = 1733₈ = 3DB₁₆ 19) 11111010₂ = 250₁₀ = 372₈ = FA₁₆

10) 110110110₂ = 438₁₀ = 666₈ = 1B6₁₆ 20) 101001010₂ = 330₁₀ = 512₈ = 14A₁₆

# 5 и 17 одинаковые или я совсем ослеп от старости? Перепроверял несколько раз,

# разницы не увидел... Обрати на это внимание.

4. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

1) 4,5178	2) 1,10108	3) 7,12348	4) 56,348	5) 123,418
6) 10,7268	7) 10,4668	8) 367,278	9) 4,7658	10) 32,5448
11) 42,1118	12) 646,238	13) 6,738	14) 73,738	15) 45,218
16) 22,778	17) 71,558	18) 10,7418	19) 61,478	20) 45,658

1) 4,654296875₁₀ 11) 34,142578125₁₀

2) 1,126953125₁₀ 12) 422,296875₁₀

3) 7,1630859375₁₀ 13) 6,921875₁₀

4) 46,4375₁₀ 14) 59,921875₁₀

5) 83,515625₁₀ 15) 37,265625₁₀

6) 8,91796875₁₀ 16) 18,984375₁₀

7) 8,60546875₁₀ 17) 57,703125₁₀

8) 247,359375₁₀ 18) 8,939453125₁₀

9) 4,978515625₁₀ 19) 49,609375₁₀

10) 26,6953125₁₀ 20) 37,828125₁₀

5. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

1) 1F16	2) ABC16	3) 101016	4) 0,А416	5) 1DE,C816
6) 45,6516	7) A2E16	8) 45F16	9) 1AB16	10) 5,AA16
11) 16,DE16	12) A6,2416	13) B2,9C16	14) 12,9C16	15) F2,9916
16) C47816	17) FF116	18) A4516	19) 45F16	20) 0,45F16

1) 31₁₀ 11) 22,8671875₁₀

2) 2748₁₀ 12) 166,140625₁₀

3) 4112₁₀ 13) 178,609375₁₀

4) 0,640625₁₀ 14) 18,609375₁₀

5) 478,78125₁₀ 15) 242,59765625₁₀

6) 69,39453125₁₀ 16) 50296₁₀

7) 2606₁₀ 17) 4081₁₀

8) 1119₁₀ 18) 2629₁₀

9) 427₁₀ 19) 1119₁₀

10) 5,6640625₁₀ 20) 0,273193359375₁₀

# 8и 19 одинаковые или я совсем ослеп от старости? Перепроверял несколько раз,

# разницы не увидел... Обрати на это внимание.

6. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты:

1) 1001111110111,01112;	2) 1011110011100,112;	3) 1110101011,10111012;
4) 10111,11111011112;	5) 10111001,1011001112;	6) 1100010101,110012.
7) 10111100001,11012	8) 1010100001,1012	9) 1100001,10101112
10) 10111001,0112	11) 100010111001,110112	12) 10001101,010112
13) 1111101,00101012	14) 10011010,011012	15) 101000110,101100012
16) 10011100110,101112	17) 100110,10111012	18) 1111100110,101012
19) 1110000110,100012	20) 1011001000,112	21) 100010010,1112

1) 11767,34 = 13F7,7₁₀ 12) 215,26 = 8D,58₁₀

2) 13634,6 = 179C,C₁₀ 13) 175,124 = 7D,2A₁₀

3) 1653,564 = 3AB,BA₁₀ 14) 232,32 = 9A,68₁₀

4) 27,7674 = 17,FBC₁₀ 15) 506,542 = 146,B1₁₀

5) 271,547 = B9,B38₁₀ 16) 2346,56 = 4E6,B8₁₀

6) 1425,62 = 315,C8₁₀ 17) 46,564 = 26,BA₁₀

7) 2741,64 = 5E1,D₁₀ 18) 1746,52 = 3E6,A8₁₀

8) 1241,5 = 2A1,A₁₀ 19) 1606,42 = 386,88₁₀

9) 141,534 = 61,AE₁₀ 20) 1310,6 = 2C8,C₁₀

10) 271,3 = B9,6₁₀ 21) 422,7 = 112,E₁₀

11) 4271,66 = 8B9,D8₁₀

7. Узнать MAC адрес компьютера и перевести его в десятичную систему счисления.

1A-3E-8E-3D-96-09 = 026-062-142-061-150-009

8. Сложить числа.

1) 10100100002+11011110112	2) 1101011012+1111111102	3) 10010002+11011010012
4) 1100100012+10011012	5) 10100111102+100010002	6) 11110012+1101001102
7) 10010011012+11110002	8) 10000000102+1101001012	9) 11000011002+10100000012
10) 1110100102+10110111102	11) 1000001012+11000010102	12) 11000112+1101110112
13) 11110110102+1110011002	14) 1001101112+1010010002	15) 11111001002+1001101112

1) 11000001011₂ 9) 10110001101₂

2) 1110101011₂ 10) 10010110000₂

3) 1110110001₂ 11) 1000001010₂

4) 111011110₂ 12) 11000110₂

5) 1100100110₂ 13) 11110110100₂

6) 1000011111₂ 14) 1001111111₂

7) 1010010111₂ 15) 10100011011₂

8) 1110100111₂

9. Сложить числа.

1) 1011101001,12+1110111,012	2) 1100110100,00112+1101110000,012
3) 1100011100,10012+10111100,12	4) 1001110001,012+1101000111,001012
5) 1000010100,0112+1111110111,0112	6) 101011011,0112+11100010,12
7) 1100011000,1012+10000010100,12	8) 11010001,012+1110110100,00112
9) 1000110,1012+1010010001,0012	10) 101100000,10012+110001101,012
11) 1111111100,110012+1011100,012	12) 1111110111,12+1101111001,012
13) 1011101011,12+1001011100,00112	14) 110100000,00112+101000110,12
15) 1101101111,1012+1010101100,0012	16) 11011110,012+100011101,01112

1) 1101100000,11₂ 9) 1011010111,11₂

2) 11010100100,0111₂ 10) 1011101101,1101₂

3) 1111011001,0001₂ 11) 10001011001,00001₂

4) 10110111000,01101₂ 12) 11101110000,11₂

5) 11000001011,11₂ 13) 10110010111,101₂

6) 1000111101,111₂ 14) 1011100110,1011₂

7) 11100101101,001₂ 15) 100110001011,11₂

8) 10010000101,0111₂ 16) 111111011,1011₂

10. Сложить числа.

1) 40A,E8(16)+92,7(16).	2) 1664,1(8)+501,3(8)	3) 477,2(8)+647,4(8);
4) 1053,34(8)+1513,2(8);	5) 29E,3(16)+D8,4(16).	6) 372,4(16)+1F0,4(16).
7) 1711,6(8)+1763,34(8);	8) 1742,4(8)+456,1(8);	9) 1213,34(8)+1012,34(8);
10) 30A,4(16)+89,48(16)	11) F7,4(16)+178,4(16).	12) 3FE,58(16)+339,7(16).
13) 1F0,6(16)+34,4(16).	14) 433,4(8)+1774,2(8);	15) 552,24(8)+1443,2(8);

1) 49,D58₁₆ 9) 2225,7₈

2) 2365,4₈ 10) 393,88₁₆

3) 1346,6₈ 11) 26F,8₁₆

4) 2566,54₈ 12) 737,C8₁₆

5) 376,7₁₆ 13) 224,A₁₆

6) 562,8₁₆ 14) 2427,6₈

7) 3675,14₈ 15) 2215,44₈

8) 2420,5₈

11. Выполнить вычитание.

1) 1110011110,00112-1011011,0112	2) 1101110101,1012-1010111110,011012	3) 1111000010,12-1110010110,012;
4) 1111110001,0012-1010011000,01112	5) 1111100001,012-111111011,0112	6) 1010111000,01012-1010001001,0012
7) 1100110000,01012-110000110,0012	8) 1111000000,0112-100011000,012	9) 101110011,112-1110001,012
10) 1111110101,0012-101100011,00112	11) 1100110100,012-101100010,1012	12) 1011011100,0112-111011111,12
13) 1101101,10112-111110,0012	14) 1101110010,012-111110110,012	15) 1110011001,10112-1101101100,112

1) 1101000010,01₂ 9) 100000010,1₂

2) 10110111,00111₂ 10) 1010010001,1111₂

3) 101100,01₂ 11) 111010001,101₂

4) 101011000,1011₂ 12) 11111100,111₂

5) 111100101,111₂ 13) 101111,1001₂

6) 101111,0011₂ 14) 101111100₂

7) 110101010,0011₂ 15) 101100,1111₂

8) 1010101000,001₂

12. Выполнить вычитание.

1) 553,28-105,58	2) 1B9,416-1B4,616.	3) 543,468-517,28
4) 298,916-67,416.	5) 1026,668-124,28	6) 284,B16-77,416.
7) 1617,48-1442,68	8) 3E0,216-1EA,216.	9) 610,28-117,28
10) 36C,216-38,516.	11) 314,548-77,148	12) 404,B816-307,416.
13) 1653,18-415,68	14) 233,6816-DB,416.	15) 30F,7816-91,816.

1) 445,5₈ 9) 471₈

2) 4,E₁₆ 10) 333,D₁₆

3) 24,26₈ 11) 215,4₈

4) 231,5₁₆ 12) FD,78₁₆

5) 702,46₈ 13) 1235,3₈

6) 20D,7₁₆ 14) 158,28₁₆

7) 154,6₈ 15) 27D,F8₁₆

8) 1F6₁₆

13. Выполнить умножение.

1) 11100002 ·10001012	2) 11000102 · 1000012	3) 10110002 · 101012
4) 11000012 · 10111002	5) 1110112 ·111102	6) 101112 · 10000012
7) 10100002 · 11010112	8) 1001012 · 1001012	9) 1111112 · 11011002
10) 11011012 · 1000002	11) 110102 ·11112	12) 11000112 · 11001002
13) 11100102 · 10101112	14) 10111102 · 11101012	15) 101112 · 101102

1) 1111000110000₂ 9) 1101010010100₂

2) 110010100010₂ 10) 110110100000₂

3) 11100111000₂ 11) 110000110₂

4) 10001011011100₂ 12) 10011010101100₂

5) 11011101010₂ 13) 10011010111110₂

6) 10111010111₂ 14) 10101011110110₂

7) 10000101110000₂ 15) 111111010₂

8) 10101011001₂

14. Выполнить умножение.

1) 2F,3816 · 37,716.	2) 1324,28 ·75,548	3) 24,416 · 5E,416.
4) 113,28 ·60,28	5) 1D,A16 · 8,416.	6) 1605,148 ·22,048
7) 4F,416 ·56,D16.	8) 242,28 · 73,28	9) 4D,A16 ·69,616.
10) 1210,28 · 5,38	11) 20,416 · 2F,416.	12) 104,548 ·66,38
13) 66,D16 ·1C,D16.	14) 1355,58 · 125,648	15) 436,28 · 57,148

1) A39,B08₁₆ 9) 1FF3,BC₁₆

2) 127205,13₈ 10) 6634,26₈

3) D58,9₁₆ 11) BDF,9₁₆

4) 7056,64₈ 12) 7226,704₈

5) F4,68₁₆ 13) B92,49₁₆

6) 37625,546₈ 14) 175507,144₈

7) 1ADF,E4₁₆ 15) 32303,33₈

8) 22615,24₈

15. Выполнить деление.

1) 100001101102 : 10112	2) 111110010112 : 101012	3) 100101011112 : 10112
4) 1101000002 : 100002	5) 100101110012 : 11012	6) 100000010002 : 11002
7) 10101111102 : 100102	8) 10010001002 : 10102	9) 111011000002 : 100002
10) 10011000002 : 100112	11) 100010011002 : 10102	12) 11101101012 : 11012
13) 111011111112 : 100112	14) 101100000102 : 11112	15) 110011001102 : 101012

1) 1100010₂ 9) 1110110₂

2) 1011111₂ 10) 100000₂

3) 1101101₂ 11) 1101110₂

4) 11010₂ 12) 1001001₂

5) 1011101₂ 13) 1100101₂

6) 1010110₂ 14) 1011110₂

7) 100111₂ 15) 1001110₂

8) 111010₂

16. Вычислите значение выражения в двоичной системе, а затем результат переведите в десятичный вид.

1) 7716-778+1112	2) 1101112/1012+ 1358	3) 1D16+728/112
4) D4516-1238+458	5) (916∙A316)/128	6) 47A16-1678
7) А116/10112-1112	8) F416∙38-10012	9) 7618-11102+FF16
10) (1018-1012)∙F16	11) 678+2116-111112	12) 1118∙3416
13) А216-1112+728	14) 55А16/1002+178	15) 102∙108+1016

1) 1110111₂-111111₂+111₂ = 111111₂ = 63₁₀

2) 110111₂/101₂+1011101₂ = 1101000₂ = 104₁₀

3) 11101₂+111010₂/11₂ = 110000₂ = 48₁₀

4) 110101000101₂-1010011₂+100101₂ = 110100010111₂ = 3351₁₀

5) (1001₂*10100011₂)/1010₂ = 10010010₂ = 146₁₀

6) 10001111010₂-1110111₂ = 10000000011₂ = 1027₁₀

7) 10100001₂/1011₂-111₂ = 111₂ = 7₁₀

8) 11110100₂*11₂-1001₂ = 1011010011₂ = 723₁₀

9) 111110001₂-1110₂+11111111₂ = 1011100010₂ = 738₁₀

10) (1000001₂-101₂)*1111₂ = 1001011000₂ = 600₁₀

11) 110111₂+100001₂-11111₂ = 111001₂ = 57₁₀

12) 1001001₂*110100₂ = 111011010100₂ = 3796₁₀

13) 10100010₂-111₂+111010₂ = 11010101₂ = 213₁₀

14) 10101011010₂/100₂+1111₂ = 101100101₂ = 357₁₀

15) 10₂*1000₂+10000₂ = 100000₂ = 32₁₀

17. Если вариант теста имеет объем 20 килобайт (на каждой странице теста 40 строк по 64 символа в строке, 1 символ занимает 8 бит), то чему равно количество страниц в тесте?

20 кбайт = 1024*20 = 20480 байт

1 страница = 40*64*8 = 20480 бит или 20480/8 = 2560 байт

20480/2560 = 8

Ответ: 8 страниц.

18. Считая, что один символ кодируется одним байтом, подсчитать в байтах количество информации, содержащееся в фразе: Привет, как дела?

Если 1 символ = 1 байт, значит количество байт в фразе = количеству символов.

Считаем символы: Привет, как дела? - 13 букв, 2 знака препинания и 2 пробела = 17 сим-

волов = 17 байт.

Ответ: 17 байт.