Совместное влияние межмодовой и материальной дисперсий

Ранее рассматривались два независимых эффекта, которые обусловлива­ли в отдельности межмодовую и материальную дисперсии. Но реально оба эф­фекта присутствуют одновременно, поэтому возникает задача, каким образом следует их объединять при определении дисперсии.

При оценке полосы пропускания оптической системы связи или макси­мальной скорости передачи необходимо учитывать форму принимаемых им­пульсов. Форма принятого импульса из-за влияния материальной дисперсии характеризует распределение мощности по длинам волн, образующих этот им­пульс. И так как оптические источники излучения в большинстве случаев име­ют гауссовское распределение по длинам волн, поэтому следует ожидать, что форма принятого импульса будет также гауссовской относительно среднего времени прихода импульса. В случае межмодовой дисперсии при распростра­нении импульса по различным траекториям можно считать, что наибольшая часть мощности переносится теми лучами, которые проходят по среднему оп­тическому пути. Поэтому уширение принятого импульса за счет межмодовой дисперсии можно также считать приблизительно гауссовской.

Предположим теперь, что уширение импульса происходит под влиянием как межмодовой, так и материальной дисперсий, что оба механизма независи­мы друг от друга и каждый из них приводит к появлению гауссовских импуль­сов длительностями τ_мм и τ_мат. Тогда в результате их совместного влияния обра­зуется импульс, который будет оставаться приближенно гауссовским по форме, а его длительность на уровне 0,5 будет определяться выражением

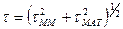. (2.48)

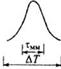
Если передаваемый импульс не бесконечно короткий, а также приблизи­тельно гауссовский с длительностью на уровне 0,5 равной τ₀, то приведенные рассуждения можно распространить и на него, как показано на рис. 2.19, и счи­тать длительность принятого импульса на уровне 0,5:

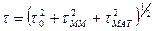, (2.49)

где τ₀- первоначальная длительность импульса; τ_мм, τ_мат - уширения импульса за счет влияния межмодовой и материальной дисперсий соответственно.

Воспользовавшись выражением (2.49), можно написать значение ушире­ния импульса, приведенное к единице длины линии:

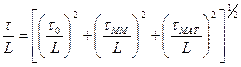. (2.50)

Здесь, как и ранее, τ₀ обозначает ширину передаваемого импульса на уровне половинной

мощности, а величины 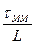и 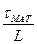учитывают влияние межмодовой и материальной дисперсий соответственно.

Импульсный Импульсный

отклик, отклик,

обусловленный обусловленный

Передаваемый межмодовой материальной Принятый
импульс дисперсией дисперсией импульс

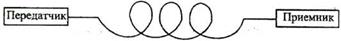Оптическое волокно

Рис. 2.19. Совместное влияние дисперсионных эффектов

Оценим совместное влияние межмодовой и материальной дисперсий в ступенчатых и градиентных ОВ на различных длинах волн для следующих зна­чений величин: τ = 0, λ = 0,9 мкм, ∆λ = 30 нм для светодиода и ∆λ = 3 нм для лазера. Для длин-волн λ = 1,3 мкм и λ = 1,55 мкм использованы значения γ = 0,04 для светодиода и γ = 0,004 для лазера. Значение межмодовой диспер­сии на уровне половинной мощности для ступенчатых ОВ составляет прибли­зительно 15 нс/км, а для градиентных ОВ соответственно 0,5 нс/км. Результаты расчета совместного влияния дисперсий представлены в табл. 2.5.

Как видно из табл. 2.5, межмодовая дисперсия преобладает во всех случа­ях при использовании ступенчатого волокна. В случае градиентного волокна при лазерном источнике будет преобладать межмодовая дисперсия. Если же применяются светодиоды, то преобладает материальная дисперсия за исключе­нием длин волн в окрестности 1,3 мкм.

Таблица 2.5

Влияние межмодовой и материальной дисперсий

в ступенчатых и градиентных кварцевых ОВ на различных длинах волн

Длина волны, мкм	Источник излучения	τмат / L, нс/км	τ / L, нс/км
ступенчатое фадиентное	градиентное
0,9	СД	2,1	2,2	2,2
Лазер	0,2	0,5	0,5
1,3	СД	0,1	0,5	0,5
Лазер	0,01	0.5	0,5
1,55	СД	1,2	1,3	1,3
Лазер	0,1		0,5

Таким образом, становится очевидным, что для достижения всех выгод, обеспечиваемых малой материальной дисперсией в окрестности 1,3 мкм, необ­ходимо уменьшить межмодовую дисперсию до значений, меньших 0,5 нс/км. Это может быть достигнуто двумя путями. Первый состоит в уменьшении диа­метра сердцевины до тех пор, пока не будет получен одномодовый режим рабо­ты. В этом случае общая дисперсия будет очень малой, ее значение составит порядка 10 нс/км. Второй путь состоит в очень тщательном профилировании показателя преломления в градиентных волокнах. Лучшие градиентные ОВ имеют межмодовую дисперсию 0,2-0,3 нс/км.